Pulse Streams and Problems of Grouping and Metrical Dissonance in Bartók’s “With Drums and Pipes”
John Roeder
KEYWORDS: rhythm, meter, pulse streams, polyphony, grouping, accent, metrical dissonance, Bartók
ABSTRACT: Polyphony has many interesting rhythmic properties that do not obtain in textures that are modeled by most rhythmic theories. This paper invokes the concept of pulse streams to demonstrate how phenomenal accent and grouping are organized in a extended two-voice polyphony by Bartók to create convincing form and process. The pulse-stream analysis is manifested audibly by Quicktime examples that combine audio playback, a scrolling annotated score, and the pulses played by percussion instruments.
Copyright © 2001 Society for Music Theory
Table of Contents
- Introduction
- Analysis of grouping and "metrical dissonance"
- Challenges to rhythmic theory raised by the analysis
- A theory to help resolve problems of polyphonic rhythm
- Pulse-stream analysis
- Analysis of mm. 30–43
- Analysis of mm. 41–53
- Analysis of mm. 56–68
- Summary and Conclusion
[1] Introduction
[1.1] Polyphony, the concurrence of two or more musical streams, has many interesting rhythmic properties. Many of them do not obtain in the monophonic or homophonic textures that are modeled by most rhythmic theories. The difference between rhythm in polyphony and in homophony becomes apparent when we consider accent and grouping, the basic, though not neatly separable, aspects of rhythm identified by Lerdahl and Jackendoff (1983), among others. It is also apparent when we consider meter, which I take here to be a mental construction of a regular hierarchy of beats in conformance with grouping structure and accentual patterns presented in the piece.
[1.2] In polyphony, accent is not simply a property of a timepoint. To the extent that any given accent arises from features of a particular stream, it must be attributable to that stream only, and not to other concurrent streams. Consequently when at any given moment more than one stream is proceeding, accent may appear in one stream and not the other. Similarly, grouping can be different in concurrent voices. In many polyphonic textures the boundaries and durations of groups in one stream are different from those in concurrent streams.
[1.3] One familiar process that may result from these rhythmic properties of polyphony is polymeter, which is familiar in the hemiolas of Handel and Brahms, but also appears ubiquitously in music from medieval polyphony to jazz. Composers in the early twentieth century, such as Stravinsky and Bartók, had a marked predilection for textures of this sort. Music theorists—most thoroughly, Harald Krebs (1987, 1997, 1999), in his adaptations of Yeston’s (1976) notions of “metrical consonance and dissonance”—have analyzed polymetric passages by investigating and classifying them according to the ways that a single underlying rapid pulse is grouped simultaneously into different “layers” or “levels” that have different characteristic durations. These investigations focus on special passages in which the groups are repeated, so that levels are maintained in each voice, and they treat the ratios of level durations as significant.
[1.4] A more complete picture of such polyphony can be obtained by considering the accentual properties of the groups in more detail. This paper will demonstrate how, in an extended two-part polyphony, streams of pulse are created by accents, how these streams interact with the rapidly changing groups in both parts, and how those interactions contribute to the processes and form of the piece.
[2] Analysis of Grouping and “Metrical Dissonance”
[2.1] The passage to be considered is taken from “With Drums and Pipes,” the first movement of the suite for piano, entitled Out of Doors, by Bartók. The music has close affinities to the first movements of Bartók’s Piano Sonata and Piano Concerto No. 1, which were composed in the same year, 1926. The score to the passage is shown in Figure 1, containing mm. 20–69. (This and subsequent Figures require the Adobe Acrobat Reader.) Clicking here (Example II.1) will bring up a window with an example that presents a complete performance, along with a scrolling score. Mm. 22–69 contain the substance of the piece. They are preceded and followed by simpler, more regular music that features a series of short melodic segments, usually a whole-note in duration, accompanied in repeated eighth notes in the very low register of the piano, as suggested by the cadential material in mm. 20–21. At m. 22 the register rises, and there unfold numerous irregularities of accent and group length. The simpler opening material returns in m. 68, so it would appear that the latter half of this central passage is designed to make this return possible and convincing.
[2.2] During much of the polyphony in mm. 22–69 we can distinguish two distinct concurrent streams, and so this passage is well suited for studying the aspects of grouping and accent in polyphony that I raised in section 1. For the performer these streams correspond to left- and right-hand parts, although the hands do not play “voices” in the sense of melodic lines with different timbres and registers. Indeed they both often play clusters, sometimes in immediate succession (as in mm. 22 or 39) and sometimes alternating with single pitches (as in mm. 26 and 56), and in register they vary considerably and overlap. Despite the occasional similarity of the two streams, however, one can indeed hear them as distinct motivically, registrally, and by how their materials group, as we shall see.
[2.3] Along with its potential for illuminating certain questions of rhythmic theory, however, the unusual nature of this texture itself merits close analysis. What is the function of this particular arrangement of these percussive materials, aside from simply evoking the beating of drums? Is this restricted texture particularly well suited for particular, form-creating musical processes? What analytical tools—what ways of hearing the music—can best elucidate its design?
[2.4] The remainder of this section of the paper will suggest some ways of answering these questions. It presents a detailed analysis, using annotated excerpts and audio clips, of the motivic material and grouping in the passage. It is intended to help the reader become familiar with the passage, and with theories of grouping and metrical dissonance that have the potential to explain it. Readers who are sufficiently familiar with the music and those theories may wish to skip ahead to Section 3, where the results of this close analysis, along with certain inadequacies of the theories, are summarized.
Example II.2. First Block
(click to watch video)
Example II.3. Second Block
(click to watch video)
Example II.4. Third Block
(click to watch video)
Example II.5. Fourth Block
(click to watch video)
Example II.6. Fifth Block
(click to watch video)
Example II.7
(click to watch video)
Example II.8. Sixth Block
(click to watch video)
Example II.9
(click to enlarge)
Example II.10. Seventh Block
(click to watch video)
Example II.11. Eighth Block
(click to watch video)
[2.5]
Because the hands tend to change motivic material at about the same time, a succession of contrasting blocks or segments arises, principally through such changes in motivic materials, supported by changes in dynamics and register. Although I will refer to timespans by measure numbers, the block divisions do not always appear on the notated downbeat, as the following discussion will explain. There are eight blocks in all. Each is discussed below, with special focus on some readily apparent aspects of grouping and “metrical dissonance.”[2.6] First Block (Example II.2) The parallelism between the beginnings of mm. 22 and 24 suggests the organization of mm 22–25 as a four-measure block, divided into two groups each lasting a whole note. The hands alternate within each measure and on the notated downbeats within each group. At first there is a durational canon between hands, at the distance of a half note, as the duration series in the right hand in mm. 22–23 is imitated by the left hand in mm. 23–24. The canon is indicated by brackets in Example II.2. In the second whole-note group, there is another canon, with the distance of imitation diminished to a quarter note, that spills into the beginning of the next block. These canons, and the irregular way the left-hand shifts octaves, and the dynamic, durational and textural emphasis given to the right-hand downbeats in mm. 23 and 25 work against the ostensible grouping regularity.
[2.7]
Second Block (Example II.3) The materials of mm. 26–29 do not obviously substantiate the notated meter, but they do group within each stream in a straightforward way. The left hand reiterates a semitone cluster every three eighth notes, in alternating registers. The right hand reiterates (although never exactly) a 5-eighth note group that is subdivided by changes of textural density and contour into 3+2. The concurrence of these groupings is an example of what Krebs (1997) calls a “grouping dissonance,” in which the eighth-note pulse is grouped into two “interpretive levels of different cardinality,” 3 and 5. The levels begin an eighth-note apart, not at the same time, so they exhibit “displacement dissonance” as well. Since there are five statements of the 3-eighth duration, and three statements of the 5-eighth group, the hands return to their original orientation just before the end of m. 29. However the sense of completion is thwarted by the omission of a left-hand attack there, and by changes to the pitches and to the locations of clusters in the right hand. These changes suggest that the effect of metrical dissonance is not the sole purpose of the passage.[2.8] Third Block
(Example II.4) Measures 30–37 are more clearly organized in retrospect than they seem at first, but characterizing its grouping and metrical dissonance does not capture this evolving organization very well. Since the material in m. 30 is unexpected and unfamiliar, a clear grouping structure emerges only after it begins to repeat in m. 32. The structure is as follows: both hands sequence a whole-note’s worth of material down twice in pitch; then the sequence fragments. The group boundaries are made clear by the nearly canonic rhythms in the two streams, indicated by corresponding colors in Example II.4. Since the boundaries do not coincide, this block exhibits displacement dissonance, although, since the preceding block was also dissonant, the significance of this characterization is not clear.[2.9] Fourth Block
(Example II.5) The sequential descent halts at the beginning of m. 38, when loud right-hand clusters combine with percussive sforzandi in the left hand. The block is clearly set off from the immediately preceding and succeeding music by its contrast, articulating a duration (a dotted-whole note) that is quite different from that of the other groups. In the context of grouping theory, this difference seems merely arbitrary. There is the brief suggestion of a grouping dissonance, however, as the left hand attacks clusters every three eighths while the right hand repeats quarter notes.[2.10] Fifth Block
(Example II.6) A change of loudness at m. 41 instigates the next block of material, which lasts through m. 47 and brings further, seemingly arbitrary changes to grouping and metrical dissonance. The right hand reiterates a durational motive,[2.11] A quarter note later, a strongly accented octave in the right hand coincides
with brief fragments in the left hand (Example II.7) that recall both the just-aborted sequence,  ,
and the right-hand materials in mm. 36–37,
,
and the right-hand materials in mm. 36–37, ![]() .
.
[2.12] Sixth Block
(Example II.8) No clear grouping structure is evident until m. 50, when another sequence begins. (Its legs are shown by the brackets in the example.) As in the sequence of mm. 31–37 (Example II.4), the groups in both hands have the same duration but their boundaries do not coincide, thus creating a displacement dissonance. At the same time, however, the contour and interval patterns in the hands recall those of mm. 41–47 (Example II.6). Specifically, as shown below in Example II.9, there is a textural inversion: the left hand of mm. 50–55 plays the same stepwise lines, terminal durational accents, and overall contour as the right-hand octaves of 41–47; and the right hand of 50–55 includes the same vertical major ninths in quarter notes, embellished with offbeat neighbor notes, that are featured in the left hand of 41–47.[2.13] Seventh Block
(Example II.10) In the eight measures from 56–63 the right hand groups clearly into whole-note-long segments by sequentially repeating the material of mm. 35–36 (see Example II.4). The left hand, however, presents groups that, despite their similar pitch-class series, vary considerably in length. The fragmentation of the right-hand motive and an alteration of the left-hand pattern lead to the final block we will consider.[2.14] Eighth Block
(Example II.11) This passage presents four measures of a sustained D2 enclosed in register by alternating clusters. This design recalls mm. 20–21 (the first two measures of Example II.1) in its cadential effect. This similarity of formal function is reinforced by the fact that the material that follows in both cases (mm. 22–25 and mm. 68–71) can be heard as metrically consonant and consistent with the notated meter. Considering these parallelisms it is puzzling that mm. 64–67 do not exhibit the metrical regularity of mm. 20–21.[3] Challenges to Rhythmic Theory Raised by the Analysis
[3.1] The analysis of Examples II.1–11 shows that concepts of grouping and metrical dissonance are indeed useful for distinguishing and relating different segments of the piece, and so for addressing those synchronic aspects of musical form. But it has also highlighted some features of the music that cannot be explained with reference to those concepts.
[3.2] For example, some moments appear to be designed specifically to obscure grouping structure, at least in the way that it is theorized in Lerdahl and Jackendoff (1983). Recall m. 30, for instance, which was discussed in connection with Examples II.3 and II.4. Since the right hand has just presented three similar 5-eighth-note-long groups, we would expect another right-hand group to begin on the next eighth-note beat, that is, on the downbeat of m. 30. But that beat has none of the properties of a group boundary—the solitary right-hand E4 does not produce any substantial change, but simply extends the preceding material. The succeeding cluster, on the second eighth of the measure, sounds more like a group beginning; but then so does the D4 in the next measure, which begins a long slurred series of notes. In other words, the music presents conflicting cues. Grouping theory is very helpful for identifying these conflicts, but it does not suggest any purpose for them.
[3.3] Another passage that challenges current rhythmic theory is mm. 38ff. (Examples II.5 and II.6). The right-hand stream (Example II.5) presents a group lasting 12 eighth notes. But the duration and coherence of this material is called into question at m. 41 (Example II.6), when the left hand imitates only the last 8 eighths, then sequences only the last 6 eighths. Since each repetition omits the beginning of the preceding group, and since the groups keep changing in duration, the parallelism between the groups is obscured. Meter is also obscured, not only by the changing group lengths but also by the lack of regular phenomenal accent. For instance, even when the right hand after m. 41 is quite regular, its long and high notes do not fall on the notated downbeats, nor do they align regularly with the varying accents in the left hand. Again, grouping theory permits a clear characterization of rhythmic structure within each separate stream. But since it describes preference rules, it provides no rationale for the multiple violations of those rules, nor does it help determine a purpose for the particular coordination of misaligned grouping and accent structures in the concurrent streams. Indeed, Lerdahl and Jackendoff acknowledge that their theory is "inadequate" except for music in which "a single grouping analysis suffices for all voices" (p. 37), which is clearly not the case here. More generally, the rapidly changing group lengths, their nonalignment with the notated meter, the overlapping extents of groups in the voices, and the sporadic accents seem to violate all the "cognitive constraints" (Lerdahl 1988) on rhythm necessary to perceive large-scale grouping and metric structures.
[3.4] While metrical dissonance theory addresses some of these inadequacies, Bartók’s music poses challenges to it as well. For example, mm. 26–29 (Example II.3) can readily be labeled as a combination of "grouping" dissonance, in which groups of different lengths (5 and 3 eighths) are played concurrently, with "displacement dissonance," in which the group beginnings do not coincide. But it does not explain why the groups of 5 and 3 are displaced from each other in this particular way, or even why group durations 5 and 3 are necessary at this point in the composition. Nor does it provide a basis for understanding why one type of metrical dissonance succeeds another. A related problem arises in the canonic passages (mm. 22–26 and 30–37, Examples II.2 and II.4): considering the apparent lack of metrical control of consonance and dissonance, what constraints or compositional goals dictate the choice of materials and the durational intervals of imitation?
[3.5] In sum, current theories of grouping and metrical dissonance are designed for music in which the accent and grouping of concurrent voices are coordinated consistently. They are not adequate for analyzing polyphonic music in which these basic aspects of rhythm are constantly varying.
[4] A Theory to Help Resolve Problems of Polyphonic Rhythm
[4.1] Many of the questions raised in the context of grouping and metrical dissonance theory about the rhythms of Bartók’s piano piece can be addressed productively by attending to the timing of phenomenal accents. (See Appendix 1 for a brief surview of the types of phenomenal accent that are pertinent to the passage at hand.) Each series of regular accents is heard as a "pulse stream," that is, as a series of repeated durations (Roeder 1994). At any given moment, several such pulse streams may be proceeding, each with its own characteristic duration. In this respect the theory resembles that of metrical dissonance. But since the accents that create a pulse stream may be located in any voice, the theory better accommodates varying polyphonic textures, even textures in which voices drop in and out, or in which there are no consistent timbral continuities at all. Moreover, rather than simply labeling the mathematical relation of the characteristic durations, pulse-stream theory treats the streams as actual rhythms that take on increasing impetus as they are reinforced by subsequent accents. That is, each pulse stream possesses musical continuity and direction, so that analysis focuses on how the pulses are created and sustained, how (once established) they interact with the grouping structures of the voices, and thus how they create musical form.
[4.2] Figure 2 gives a pulse-stream analysis of the first eleven measures of the passage at hand. The score is shown in the center of the example. Above and below the score, placed to clarify certain relations with the actual music, are shown various pulses that arise from regularities of phenomenal accent. Each horizontal line represents a pulse stream that is created when at least two equal timespans are marked off by three accented timepoints.
[4.3] The figure shows that for a pulse stream to be sustained it must be constantly reinforced, more so in the presence of conflicting accents, and less so the longer it has been in existence. Consider, for example, the quarter-note pulse stream (numbered 1) created at the beginning of the passage. Its first three durations arise from fairly clear accents—an accent of inter-onset duration at the first -left-hand attack, then another left-hand attack, then a dynamic accent in the right hand. But its next duration is articulated quite weakly—only by the unaccented attack of the right hand—and so are several of its subsequent durations. The weakness is symbolized on the line that indicates the stream by enclosing these durations in parentheses. Indeed, in m. 26 stream 1 disappears quickly in the absence of a sustaining accent and in the presence of strong contradictory accents. This can be heard in audio Example IV.7, in which the quarter-note pulse (1) and the dotted-quarter pulse (4) that displaces it in m. 26 are doubled by snare drum and whistle, respectively. (The instruments that double the pulse streams in this and subsequent examples, selected from the General MIDI drum kit, allude to Bartók’s title for this piece.)
[4.4] Some pulse streams in Figure 2 feature durations that correspond exactly to the grouping structures that have been identified in the analysis above, for example, the 5-eighth-note pulse stream (labeled 5) in mm. 26–29. This occurs naturally in repetitive passages, since phenomenal accent creates group boundaries (Lerdahl and Jackendoff 1983, 46). A pulse stream may also correspond to a succession of strong beats in a regular meter, as is evident at the beginning of this passage, when the phenomenal accents do. On the other hand, since the pulse-stream analysis is nonhierarchical, a pulse stream may connect timepoints that are weak beats in a metrical reading, if those beats take phenomenal accent. This is evident at the top of the Figure 2, where odd- and even-numbered down beats are assigned to distinct whole-note pulse streams (numbered 2 and 3), as will be discussed below. Obviously, such a reading goes against our preference for hierarchical meter, but when such meter is absent, or when accentual cues give more emphasis than expected to ostensibly weak beats, a pulse-stream analysis provides an attractive explanation of the musical continuity.
[5] Pulse-stream Analysis
[5.1] To get a grasp of the analytical method, and to begin to see how it addresses the problems of analyzing polyphony, let us consider Figure 2 in more detail.
[5.2] In addition to the quarter-note pulse stream (1) that we have already discussed, the first block of the passage presents accents every half note. The second and fourth of these accents, corresponding to the dynamically accented downbeats of mm. 23 and 25, are considered in the analysis to mark off a whole-note duration. A whole note later, on the downbeat of m. 27, the reappearance m. 25’s verticality creates pulse stream 3. This pulse stream persists through the example. In contrast, pulse stream 2—which in a metric analysis would constitute the strong beats of a 2/2 hypermeter—is created by weaker accents at first. Almost immediately after it is established in m. 25 it begins to deteriorate, and it completely evaporates by m. 30, when no accent at all is provided to sustain it. In the next audio example (Example V.1), streams 2 and 3 are doubled by low and high cymbals, respectively, and the ascendance of stream 3 over the fading stream 2 is quite vivid.
[5.3] The disappearance of stream 2 signals an important point in the form of the passage, namely, the beginning of the third block of material we identified in our earlier grouping analysis. Analyzing these accents nonhierarchically as the combination of two pulses that vary in presence and strength expresses the continuity and change in the passage better than does either a metrical analysis, which would collapse the two pulses into a simple alternation of strong and weak beats, or a metrical-dissonance analysis, which would recognize the "displacement" dissonance of the two streams (Krebs 1997) but would not account for their changing strength and correlation with the form.
[5.4]
Recall that some interesting questions about the second block of material (mm. 25–30) were raised in the preliminary analysis: why are groups aligned the way they are? and what is the purpose of the changes in the material? Some answers can be given in the context of the pulse-stream analysis of Figure 2, by considering two timepoints when pulse streams intersect, timepoints, that is, that belong to more than one pulse stream.[5.5] Listen to the next audio example (Example V.2), in which streams 2, 4 and 5 are doubled by cymbals, whistle, and bell, respectively. Listen especially to the stream intersections in mm. 25 and 26, marked by the simultaneous attack of two of these pulse-representatives. To start the example playing at the downbeat of m. 25, midway through the example, drag the slider below until the second score page appears, then press the play (forward-arrow) button.
[5.6] Let us consider the purpose of the first coincidence of pulse streams,
at the notated downbeat of m. 26. The phenomenal accent then firmly establishes
stream 2, as it is the third in a series of phenomenal accents separated by
the duration of a whole note. But the same timepoint is heard (certainly in
retrospect, after three {D3,
[5.7] Concurrently with the dotted-half stream 4, a 5-eighth-note stream, labeled 5, begins to arise from accents of registral-density (and contour) at the beginning of each right-hand group in this second block. Its characteristic duration is articulated by the beginning of the first repetition of the right-hand group, on the second beat of m. 27. But this timepoint is also a dotted-half after the strong accent on the downbeat of m. 26. In other words, the left- and right-hand groups are aligned in this particular way in order to ensure the clear articulation of pulse stream 4—which, as we shall presently discover, is an important source of large-scale continuity in this passage.
[5.8] The second block is thus articulated by rhythmic contrast, in that its
ensemble of pulse streams—featuring the durations of dotted-half (4) and 5-eighth-notes
(5)—are very different from those in the first block. Nevertheless, as we have
observed in connection with Example V.1, the whole-note stream 3 acts as an
agent of rhythmic continuity through the otherwise disconnected blocks. This
stream is sustained on the downbeat of m. 27 by the cluster that divides the
first right-hand group into 3+2, then by the last attack of the upper {D,
[5.9] In the complete analysis of Figure 2, the stream label 4 is used to name both the dotted-half stream and a synchronized dotted-quarter stream. This faster stream is sustained throughout the remainder of the second block, first by regular left-hand attacks up until the end of m. 29, and then, when the left hand unexpectedly fails to repeat its dyad again, by a registral-density accent in the right hand. This accent would not have arisen had the right-hand group repeated exactly. Thus it seems that one purpose for the changes in the right-hand groups is to sustain stream 4 even as the left hand is pausing in preparation for the introduction of new material.
[5.10]
As part of the transition to the third block (m. 30), the variations in the right-hand groups in mm. 28–30 also create other pulse streams. The verbal annotations on Figure 2 indicate the nature of the changes, which withhold accents of registral density from certain times we would expect them, and add an unaccented E4 at the downbeat of m. 30. Stream 6 arises from the reiteration of registral-density accents in the right hand every quarter note, but disappears at the onset of new material. Stream 7, in hemiola with pulse 6, arises from registral-density and contour accents in the right hand, and is continued by the first durational accent in the new material in the left hand at the downbeat of m. 31.[5.11] While these two pulse streams are clear continuities in their own right, they render the rhythmic texture considerably more "dissonant," an effect that is resolved as the accents necessary to sustain them are withheld in mm. 31–32, and as an ensemble of pulse streams recalling those in the first block is reestablished: the quarter-note stream 1, by accents of registral density in both hands; whole-note stream 3 (which has remained constant throughout), by durational accents in the left hand; and another whole-note stream, labeled 8 in the score, arising from the regularly spaced greatest accents in the right hand.
[5.12] In the next audio example (Example V.3a) all the pulse streams are represented by the "drums and pipes." Their complex combination can best be studied by listening to each percussion instrument as it enters and exits.
[5.13]
The following example (Example V.3b) presents the same analysis, but omits the underlying piano music, so that the stream combination can be heard more readily.[5.14] The changes in the right-hand groups at the end of the second block are thus precisely designed to effect a smooth transition—despite the contrast of material—to the pulse-stream ensemble of the third block. At first, stream 6 evens out the irregularly accented right-hand groups into an evenly accented stream. Then a sense of order is restored at the downbeat of m. 31, where streams 7 and 3 coincide for the first time, and the original quarter-note stream 1 reemerges.
[6] Analysis of mm. 30–43
[6.1] Figures 3–5 present pulse-stream analyses of the remainder of Figure 1. In the following sections I will briefly discuss how pulse streams are created both within the two hands/voices and between them, and how the streams function formally to create both contrast between successive blocks of material and rhythmic continuity.
[6.2] Figure 3 analyzes mm. 30–43, including the third and fourth blocks of material and the beginning of the fifth. Recall that in the third block, mm. 30–37, the two hands are in a near-canon, placing their durational accents a half-note apart. The analysis treats these accents, as in the first block, as the result of two whole-note streams of varying strength. Stream 8, which was evident in Figure 2, includes (among others) the right-hand accents, and it persists until the fifth block is well underway. The other whole-note stream, 9, includes the left-hand accents of inter-onset duration on the last events of each leg in the sequence; it is sustained only in the third block, that is, the lack of accent to sustain it in m. 37 helps prepare for the change of material in m. 38.
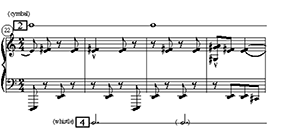
[6.3] Although within each voice the accents give rise to distinct pulse streams, they are also coordinated between the hands to maintain weakly the dotted-half stream 4 that was initiated in the second block (mm. 26–29 on Figure 2). The purpose of maintaining this stream becomes evident at the onset of the fourth block, on the downbeat of m. 38. The attack of the loud clusters there coincides with stream 4, maintaining a rhythmic continuity across the abrupt change of loudness, register, and motivic material. Stream 4 even persists into the next block (beginning at m. 41), sustained by the reiteration of durationally accented tenuto ninths in the left hand a dotted-half apart. Like stream 8, then, it is an agent of continuity.
Example VI.1
(click to watch video)
Example VI.2a
(click to watch video)
Example VI.2b
(click to watch video)
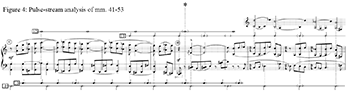
Figure 4. Pulse-stream analysis of mm. 41–53
(click to enlarge)
[6.4] In the following audio presentation (Example VI.1) of Figure 3, stream 4 is doubled by a whistle, while whole-note streams 8 and 9 are doubled by differently pitched cymbals. As was the case in Figure 2, regarding the changing ensemble of pulse streams across Figure 3, we see that each new block of material is characterized by a different ensemble.
[6.5]
Reconsidering mm. 35–36, we see that the changes to the material in both hands that disrupt the third leg of the sequence also initiate a new pulse stream that maintains rhythmic continuity into the next contrasting block. This stream, labeled 10 at the bottom of Figure 3, features the duration of a dotted-quarter. In the following audio example (Example VI.2a) of mm. 34–42, stream 10 is doubled by a drum, and the other streams are presented as above.[6.6] Although there are silences at two points where one would expect this stream to be sustained—on the last beats of mm. 37 and 40—the stream is nevertheless clear. In this analysis, the sfozando left-hand dyads in mm. 38–40, which on paper appear quite disruptive, strengthen this stream as an agent of continuity and, as part of the stream, are prepared by the accents in mm. 35–37 that initiate the stream. Moreover the quarter-note pulse stream that is audible in m. 30 (but which is not explicitly shown in the analysis) is analyzed as the resultant rhythm of several slower streams that are not synchronized among themselves, but that include the most accented timepoints in the music. So this analysis clarifies the function of this otherwise odd three-measure eruption as an important rhythmic transition between the longer sequential blocks preceding and following it.
[6.7]
The following example (Example VI.2b) presents the same analysis, but omits the underlying piano music, so that the stream combination can be heard more readily.[7] Analysis of mm. 41–53
[7.1] Figure 4 continues the pulse stream analysis of the block that starts in m. 41. Three principal streams are identified. Streams 4 (recurring every dotted half) and 10 (recurring every dotted quarter), which were initiated in the previous blocks, are here continued by durational accents and by the sequential change from one vertical left-hand dyad to the next. They are supported by the unusual notation in the left-hand part: normally the last note in a slurred group is not stressed, but Bartók specifies a tenuto on the last dyad of each of the left-hand groups. This requires the performer to bring out the dyad, thereby maintaining stream 4, while still maintaining stream 10 with the regular group-beginnings of the sequence.
[7.2] A new whole-note stream, labeled 12, is created by the three durational accents in the right-hand melody. The block is cut off abruptly by a loud low dyad in the left hand at m. 48, recalling mm. 38–40. This dyad is obviously disruptive in some ways, but it also is an agent of continuity. As streams 4 and 10 proceed in the preceding block, we are aware of the duration of a half note between the onset of each new vertical dyad and the later, durationally accented statement of the same dyad. In particular, at m. 46, as shown by the dotted vertical lines, there is a half note from the onset of the D2–E3 dyad to the durational accent statement of it. The loud dyad at the downbeat of m. 48 provides accent in an unexpected location—interrupting the expected continuation of the left-hand group—but since it is a half note after the last durational accent, it creates a new half-note pulse stream, labeled 13.
Example VII.1a
(click to watch video)
Example VII.1b
(click to watch video)
Example VII.2
(click to enlarge)
Figure 5. Pulse-stream analysis of mm. 56–68
(click to enlarge)
Example VIII.1a
(click to watch video)
Example VIII.1b
(click to watch video)
[7.3] The following audio example (Example VII.1a) doubles these pulse streams with drums and pipes, as before.
[7.4]
The next example (Example VII.1b) sounds only the percussion doublings of the streams, without the piano part. It makes the changes in stream combinations from one block to the next especially vivid.[7.5] As the new material of the next block is established, the new pulse stream 13 is sustained by the interaction of accents in the two hands. At first it corresponds to the notated downbeats, but it persists even when the meter signature starts to vary in m. 51. The right-hand side of Figure 4 identifies three sources of accent in this passage: the accent of dyad change in the right hand, as suggested by the reduction in the staff above the score; the durational accent in the left-hand melody, and the weaker accents of registral density when three pitches are attacked simultaneously. The vertical dotted lines cutting across stream 13 show how it is sustained by the regular succession of accents of these three types in alternation. Stream 4 is similarly maintained across the change of material, first through the durationally accented D octaves in m. 48, then through the regularly spaced but different types of accent in both voices, as shown by the vertical dotted lines in the figure.
[7.6] A small compositional inconsistency in m. 50 seems puzzling at first glance. Comparing the first leg of the sequence in the right hand, which begins at this point, with the later legs, as in the example below, we observe that Bartók treats the incipits differently. In the first leg, the first attack has a vertical dyad and the second attack has a single note, whereas in all subsequent legs the dyad appears on the second attack.
[7.7] Figure 4 suggests a reason for this difference. The initial dyad in the first leg, m. 50, appears exactly in time to sustain whole-note stream 12, which would otherwise vanish. The lack of accent on the second attack helps put a stop to the dotted-quarter stream 10. That stream has persisted for some time now, and it could easily be heard to continue into the next block if an accent were provided here. Rather, the accent of the first attack ensures continuity from one block to the next, by sustaining stream 12 one last time. Moreover the lack of accent on the second attack creates a contrast of stream-ensemble content between the blocks, by halting a previously prominent stream.
[8] Analysis of mm. 56–68
[8.1] Figure 5, which shows the transition to the closing block in this passage, provides further examples of how pulse streams organize the disparate accent structures of the different voices in the polyphony, and provide continuity between blocks. An audio version follows (Example VIII.1a).
[8.2] The beginning of the example shows the most salient slow pulse stream
after m. 56: a whole-note stream, labeled 14, that arises from the change from
one dyad to another in the descending sequence in the right hand. (In the audio
example, these long dyads are played by low flutes.) At m. 61, the rate of change
of this dyad accelerates, so that the changes start to come a dotted-half note
apart. The attack of the long D2 (m. 64) arrives a dotted-half after the last
change of dyad, thereby initiating a dotted-half stream, labeled 15, that replaces
stream 14. The low loud dyads in mm. 65–66, although they appear to be syncopated
against the notated meter, in fact align with and reinforce stream 15. The stream
even spills into the next block—the low dyad in the last measure of the example
is a dotted-half note from the last attack of stream 15 at the downbeat of the
previous bar.
[8.3] Against both pulses 14 and 15 are presented series of regularly changing
durations. These are not pulse streams, so they are shown as series of durations
on dotted horizontal lines in the example. (They are doubled by cymbals in the
audio example.) In mm. 57–60, the timespan between durationally accented F2s
in the left hand increases each time by a quarter note. In mm. 62–66 the timespan
between the onset of the eighth-note dyad decreases each time by an eighth.
[8.4]
Thus once again we see a block of music distinguished from its surrounding blocks by a unique ensemble of pulse streams. The contrast is made especially vivid by the following audio example (Example VIII.1b), which presents only the "drums and pipes" doublings of the pulse stream, omitting the piano part.[8.5] At the beginning of the example, the quarter–note stream 1 is articulated by repeated accents of registral density, along with stream 14 and the decelerating duration series. At m. 64, however, streams 1 and 14 disappear, replaced by 15 , until the last measure of the blocks, when stream 1 is reinstated as stream 15 provides continuity.
[8.6] The asterisks above the score in Figure 5, and in the previous figures, call attention to a device that often recurs in this passage to signal the change from one block to another. Bartók tends to place a strong phenomenal accent an eighth note before or after the timepoint when the rearticulation of a prominent pulse stream is expected, but withheld. This is evident at mm. 30, 38, 48, as well as here. The strong accent usually initiates a new stream distinctive to the upcoming block.
[9] Summary and Conclusion
[9.1] This paper began by considering what a rhythmic analysis of this passage would entail. Although the music segments readily into blocks, we discovered difficulties in characterizing those blocks and the rhythmic continuity using theories of grouping, meter, and metrical dissonance. The problems arose partly because the music is a polyphony in which the voices are not coordinated in a consistent meter, and partly because of the changing rhythms within each voice itself. Some blocks could be described as exhibiting various types of metrical dissonance, but such labels did not seem to account for the specific alignment of groups or accents within each block, nor explain the rhythmic continuity across block boundaries.
[9.2] Pulse-stream theory offers a basis for resolving these difficulties, and thereby leads to a more detailed understanding of the rhythmic aspects of this passage. Accents from the distinct, concurrent voices in the polyphony are heard to create concurrent streams of pulse, moving at various tempi. This analysis helps characterize blocks very specifically, as each block features a distinctive ensemble of pulse streams. It explains the particular alignment of groups within metrically dissonant blocks as contributing to the pulse-stream ensemble. It accounts for the musical continuity in situations where a pulse stream continues across block boundaries, and also reveals special modes of block boundary articulation, such as the dissipation of a pulse stream that is characteristic of a block just before the block ends.
[9.3] Most importantly, the theory helps deepen our appreciation of Bartók’s control of rhythm in a composition where he seems to have imposed restrictions on materials and medium deliberately, in order to focus his and our attention on this most immediate of musical perceptions.
Appendix 1
Phenomenal Accent
The term "phenomenal accent" is taken from Lerdahl and Jackendoff (1983: 17). It arises at timepoints of marked change in any of the perceived properties of sound—duration, loudness, timbre, and pitch. Here are a few examples, taken from the music under consideration. A timepoint is relatively accented if it initiates a long duration following short durations in a voice, such as the second eighth-beat of m. 30 (Example IV.1). A timepoint may also take accent due to sudden increase in loudness (such as on the first beat of m. 23 in Example IV.2) or in registral density (such as the four-pitch cluster in m. 32 in Example IV.3), or due to a sudden change of register in a voice (such as the left-hand dyad on the down-beat of m. 26 in Example IV.4). A peak in the melodic contour may also produce some accent, as on the onset of A4 in m. 29 in Example IV.5 Of course, more than one factor may combine to create accent, for example on the downbeat of m. 25, which is accented by loudness, registral density, and contour (see Example IV.6).
|
Example IV.1. A timepoint is relatively accented if it initiates a long duration following short durations in a voice, such as the second eighth-beat of m. 30 (click to watch video) |
Example IV.2. A timepoint may also take accent due to sudden increase in loudness (such as on the first beat of m. 23) (click to watch video) | |
|
Example IV.3. Or in registral density (click to watch video) |
Example IV.4. Or due to a sudden change of register in a voice (such as the left-hand dyad on the down-beat of m. 26) (click to watch video) | |
|
Example IV.5. A peak in the melodic contour may also produce some accent, as on the onset of A4 in m. 29 (click to watch video) |
Example IV.6. Of course, more than one factor may combine to create accent, for example on the downbeat of m. 26, which is accented by loudness, registral density, and contour (click to watch video) |
John Roeder
School of Music
University of British Columbia
6361 Memorial Road
Vancouver, B.C.
V6T 1Z2 CANADA
jroeder@interchange.ubc.ca
Works Cited
Lerdahl, Fred. 1988. “Cognitive Constraints on Compositional Systems.” In Generative Processes in Music, edited by John A. Sloboda, 231–259. Oxford: Clarendon Press.
—————. 1983. A Generative Theory of Tonal Music. Cambridge, Mass.: MIT Press.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. New York: Oxford University Press.
—————. 1997. “Robert Schumann’s Metrical Revisions.” Music Theory Spectrum 19: 35–54.
—————. 1987. “Some Extensions of the Concepts of Metrical Consonance and Dissonance.” Journal of Music Theory 31.1: 99–120.
Roeder, John. 1994. “Interacting Pulse Streams in Schoenberg’s Atonal Polyphony.” Music Theory Spectrum 16.2: 231–249.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. New Haven: Yale University Press.
Copyright Statement
Copyright © 2001 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Eric Isaacson, Editor and Tahirih Motazedian, Editorial Assistant