Timing and Meter in Mande Drumming from Mali *
Rainer Polak and Justin London
KEYWORDS: Africa, Cross cultural analysis, Rhythm and meter, Non-isochrony, Microtiming/Expressive timing
ABSTRACT: This paper focuses on two pieces, “Ngòn Fariman” and “Bire,” representatives of two ethnically and regionally specific styles of Mande dance music from Mali, Bambara and Khasonka drumming. After introducing their performance contexts, instrumentation, and the basic roles of each part in their respective ensembles (i.e., the core metrical accompaniment, the piece-determining “hook,” and the improvising and regulative lead drum), timing data from several performances of each piece are analyzed, providing evidence of discrete categories of beat subdivision (Long vs. Short) as well as evidence of expressive variations within each category. The effects of a large-scale structural acceleration, characteristic of Malian drumming, and the presence of performer-specific microtiming patterns are also assessed. The implications of subdivision timing in Mande drumming for more general theories of metric well formedness are discussed, and we argue that such theories require a broader sense of (a) how non-isochrony may be integrated into a metrical framework, and (b) how metric theories need to reflect level-specific aspects of well-formedness. We also posit that the timing of beat subdivisions in Mande drumming have analogs in other music, most notably the “swing ratio” in jazz.
Copyright © 2014 Society for Music Theory
Table of Contents
- Section 1: Problem, approach, and aim [1]
- Section 2: Research context and methodology [9]
- Section 3: Drum orchestras, ensemble parts, and polyrhythms [20]
- 3.1 The drum orchestras [21]
- 3.2 Accompaniment [23]
- 3.3 Hook [29]
- 3.4 Lead [37]
- Section 4: The timing of accompaniment motives [44]
- Section 5: The timing of hook themes [63]
- Section 6: The timing of lead-drum phrases [73]
- Section 7: Conclusion [92]
Section 1: Problem, approach, and aim
Video 1.1. Lansina Diakite Trio plays Ngòn Fariman, a standard piece of the Segu Bambara drumming tradition
(click to watch video)
[1] Here is a short example of Mande drumming from Mali (Video 1.1)(1).
[2] Whether Malian or not, most listeners will have no difficulty in finding the beat and meter in this music, its dense and complex rhythmic surface notwithstanding. For the music theorist, however, this music presents a number of metrical challenges. The isochronous (even) beats in Mande drumming are composed of non-isochronous (uneven) subdivisions, and, we will argue, these subdivisions are categorically distinct. Hence they should be regarded as separate beat-interval classes (or more precisely, subdivision-interval classes).(2) Given the rapid tempi of these pieces, these non-isochronous subdivisions cannot be defined quantitatively, that is, as concatenations of a more rapid metrical substrate. Moreover, the virtuoso drummers of the Mande ensembles, especially in the lead drum, will execute a variety of flams, rolls, and other ornaments, many of which also exceed the limits of metric intelligibility.
[3] Thus the Mande drumming ensemble repertoire is a rich source for those who study rhythm and meter, be they performers, ethnomusicologists, music theorists, or music psychologists. Our aim here is twofold: (1) to examine some particular problems of metric well-formedness––specifically how to account for non-isochronous subdivisions and their nesting into the metric hierarchy, and (2) to consider how the Mande metric system can be integrated in the emerging body of analytical studies of world music (see Tenzer 2006) as well as more general theories of rhythm and meter.
[4] Non-isochronous rhythms, such as those that involve uneven beats (e.g., aksak or Bulgarian meters) or asymmetrical organizations such as 5/4 have long been a problem for Western theories of rhythm and meter. Initially, this problem was solved by denying the existence of such rhythms (see Mirka 2009 on the remarks of eighteenth-century theorists, and Arlin 2000 regarding their nineteenth-century counterparts). Indeed, for any theory of rhythm and/or meter that had symmetry as its basis (e.g., Momigny [1821] 1980; Hauptmann 1888; Riemann 1903), non-isochrony is an intractable problem. Likewise, the musical styles and traditions that employ non-isochronous rhythms had not been the purview of most discussions of rhythm and meter by Western music theorists until the end of the twentieth century. Thus non-isochronous meters are not considered by Cooper and Meyer (1960), Yeston (1976), or Lerdahl and Jackendoff (1983). Non-isochronous meters are similarly a problem for projective theories of meter, such as Hasty 1997 (for a relevant yet sympathetic critique see Stover 2009, 179–84).
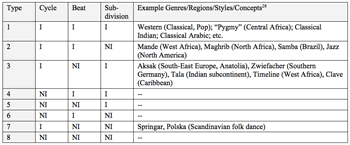
[5] Recently a few more general approaches to rhythm and meter (London 2012; Temperley 2000) have addressed non-isochronous rhythms, and such rhythms have long been acknowledged in the ethnomusicological literature (Brǎiloiu 1984; Hood 1982; Pantaleoni 1972; Kolinski 1973; Stone 1985; Kubik 1988; Arom 2004; Clayton 2000). In order to meet the fundamental requirement of some minimum degree of regularity for a functional meter, in these approaches an asymmetrically timed or non-isochronous layer of metrical structure is yoked to an isochronous stream of articulations on a lower level (e.g., Hood’s “density referent,” Kubik’s “Elementarpulsation,” Arom’s “minimal operational values,” or London’s “N-cycle”). Constraining the subdivision and beat-level timings in this fashion helps to ensure that the resultant meter will be maximally even and hence regular enough to afford entrainment (London 2012, 125–31). Kvifte (2007) and Johansson (2009), however, discuss counterexamples to this hypothesis in folk dance music from northern Europe, where metric beat and subdivision all at the same time can be non-isochronous.
[6] Mande drumming is beat based: that is, its rhythm patterns and their timings are tied to the lower levels of meter, especially levels of beat subdivision. There is a high overall ensemble density, often resulting in a saturation of the rhythmic texture, so that the composite rhythm (Lester 1986) of the ensemble articulates each and every subdivision. Mande dance drumming involves a structural acceleration in almost all styles and pieces; this accelerando is mostly very drastic, and it may be gradual and continuous, or it may be more markedly stepwise. While the beats at the tactus level are isochronous (and indeed, performed with a remarkably small degree of expressive variation, as we document below), the beat subdivisions are not—yet, at the same time, they are too rapid to be based on an even faster isochronous substrate. This motivates us to refine our theoretical account of meter to include non-isochronous patterns at the foundation of rhythm and meter. Mande drumming also shows that non-isochronous metrical structures may be more robust than previously thought (cf. London 2012, 150).
[7] Our account of expressive timing in this repertoire enriches our understanding of timing and its effect on metrical structure, including both the possibility of irrational (non-integer ratio) relationships between and within metrical levels and the possibility of some hierarchical slippage in the organization of the lower levels of meter. Our approach in this paper is interdisciplinary and interpersonally collaborative. It combines perspectives of ethnomusicology and comparative musicology (from Polak) with music theory and music psychology (London), and expands on previous works by London (1995; 2012), Polak (1998; 2010), and their exchange (London 2010 [comment]). It is empirical, based on field recordings of drumming performances, precise measurements, and statistical analyses of their timings. It is analytical, in that it is grounded on transcriptions and analyses of individual pieces. Our broader aim in this paper is to contribute to a post-ethnocentric music theory, one that acknowledges both differences and similarities between musical styles and tries to understand both their culturally specific and universal aspects.
[8] The paper will proceed in the following fashion. First, we will give details of our musical colleagues in Mali, our fieldwork with them, and technical aspects of our data collection (Section 2). Then we will provide the reader with an introduction to Mande percussion ensembles and the roles of the various instruments in each (Section 3). The bulk of the paper (Sections 4–6) involves detailed timing analyses of the principal rhythmic layers in two Mande pieces, “Ngòn Fariman” and “Bire.” Each section focuses on a particular rhythmic layer, and they provide the primary evidence for our claim that the metrical hierarchy in these pieces is based on a foundation of non-isochronous beat subdivisions. The coordination and interaction among these layers is also discussed in these sections. The paper concludes with a number of perceptual, stylistic, and theoretical arguments drawn from our observations (Section 7).
Section 2: Research context and methodology
[9] The present article is based on the analysis of field recordings made by author Polak in Mali from January to March 2012 and in December 2012. The recordings document two contemporary styles of dance music from Mali, namely bòn drumming of the Bamana people from the region of Segu in central Mali and dundunba drumming of the Khasonka people from the Khaso region in western Mali. Bamana (also: Bambara) and Khasonka (also: Xasonka, Kasonke) are ethno-linguistic groups which belong to a cluster of historically, linguistically, and culturally related peoples from Mali and neighboring countries, called Mande, or Manding (Mandingue, in French). Traditional Mande drum ensemble music involves interaction with song and dance, and may also involve masquerade. Occasions range from participatory social gatherings, such as wedding celebrations, to representative public performances. In each case, the percussion frames the social event (Polak 2007). Its presence separates celebration from everyday life and its musical form regulates the artistic interaction.
[10] Polak received practical instruction by local specialist drummers, and participated in their rehearsals, performances and daily lives. Fieldwork on Bamana drumming took place in Kirango, a former village now part of the small town of Markala, some 30 km north of the regional capital Segu. The location is known throughout the nation for its proficient tradition of masquerade sponsored by local youth associations, which is well documented (see Arnoldi 1995; Otter 1998-CD; Otter and Kéïta 2002). In Kirango, Polak worked with the expert drummers Sidiki Diarra and Boukader Coulibaly. Fieldwork on Khasonka drumming took place in Mahina, a small town close to the regional administrative center Bafoulabe, where the confluence of two large headwaters marks the origin of the river Senegal. Mahina lies in the heart of the Khaso region and is known for its strong tradition of Khasonka drumming. Polak collaborated with two professional dundunba players in Mahina: Koly Sacko and his younger brother, Toutou Sacko.
[11] Fieldwork profited from Polak’s fluency in the Bamana language, the lingua franca in Mali, and his participatory research on jembe drumming and other styles of percussion ensemble music in southern Mali for over 20 years. As Bamana bòn and Khasonka dundunba styles represent major influences on the historical development of jembe drumming in the capital Bamako, where Polak did most of his research, he also had some prior exposure to these styles.
2.1 Our sample of analytical studio recordings
[12] Polak recorded several studio performances of a repertoire of twelve standard pieces. The particular aim of the studio recordings, aside from creating documents for ethnographic and music analysis, was to acquire audio data which allow the timing analysis of individual ensemble parts. To this end, the individual instruments of the drum ensembles were close miked with four AKG C-419 unidirectional condenser clip-on microphones and recorded to separate tracks (at 48.000Hz/24Bit) with an Edirol R-4 four-track studio. Recording sessions were simultaneously filmed (at full HD/50p) with a Sony HDR-CX690 Camcorder, with supplemental audio from a Sony PCM-M10 recorder from a Rode NT-4 stereo microphone. Our primary aim was to capture performances in near-natural settings. We thus discarded approaches unfamiliar to the musicians, such as overdubbing or isolating performers in separate rooms. Only live ensemble playing was recorded, even in the studio setting. The acoustical leakage of one instrument to another instrument’s microphone thus could not be avoided completely, yet the cross-channel bleed turned out to be sufficiently low to largely preserve the note onsets of the target instruments in each separate track.
[13] Two pieces were selected for detailed analysis: Ngòn, representing Bamana bòn drumming, and Bire as typical of the Khasonka dundunba tradition.
Video 2.1. Ngòn masquerade performance in Kirango, Mali (click to watch video) | Video 2.2. Jeli Dòn dance performance in Mahina, Mali (click to watch video) |
[14] Ngòn, or Ngòn Fariman, “the (mean) chimpanzee,” relates to an entertaining mask as well as to associated repertoires of song and non-masked dance. The masquerade portrays a nasty, sexually harassing character. On a day of celebration, the performers of Ngòn “go around Kirango to pay important people a visit and announce the beginning of the masquerade” (Otter 1998, CD booklet). When it comes to public performance, Ngòn is the first mask to appear. Video 1.1, above, featured an instrumental studio version of the piece; Video 2.1 presents an excerpt of a masquerade performance.
[15] Bire is a prominent piece of the Khasonka dundunba tradition. It makes part of a suite called Jeli Dòn, “dance of the griots.” The lead Khasonka drummers featured in this article, the Sacko brothers, are griots, a social group that in Mande societies specializes in oral history, folklore, performing arts, and social mediation. Video 2.2 puts together three snippets of a Jeli Dòn live performance; Bire constitutes the middle part (0:55–1:30).
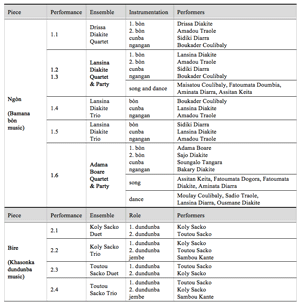
Table 2.1. Corpus of analyzed recordings
(click to enlarge)
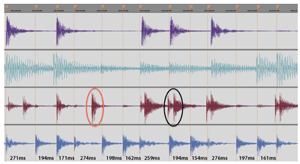
Figure 2.1. Screenshot of four-track audio of one randomly chosen four-beat cycle containing twelve subdivision elements
(click to enlarge)
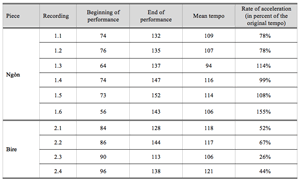
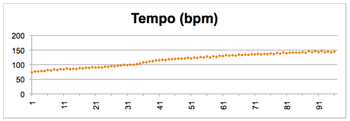
Table 2.2. Beat tempo acceleration in analyzed recordings (in bpm)
(click to enlarge)
[16] Criteria for the selection of the two pieces, Ngòn and Bire, were social importance and musical typicality. Table 2.1 lists our studio recordings, which have a total playing time of about 40 minutes. Note that some performances involve only the drum ensemble in isolation while others involve singers and dancers as well.
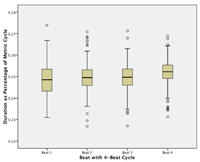
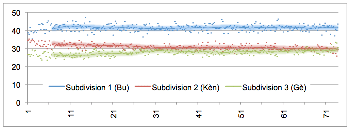
2.2 Timing data extraction and analysis
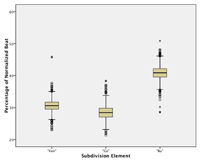
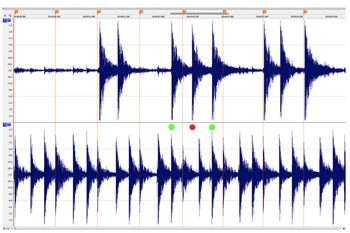
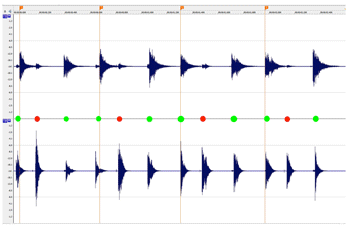
[17] We used Vegas Pro 11 and 12 (Sony) for video and audio synchronizing, archiving, and editing, and Soundforge Pro 10 (Sony) and Wavelab 7 (Steinberg) for audio editing and automatic onset (attack point) detection. Over 20,000 individual onset markers of individual drum strokes were checked by eye and manually adjusted where necessary. An example of the Vegas Pro environment and onset marking is given in Figure 2.1. After onset detection and marking, the markers’ time-points were converted into a text file and then imported into Excel for formatting and cleanup. Figure 2.1 also illustrates other aspects of Mande performance, including the regulative accompaniment part (the bottom track in the figure), the alignment (and rarer but significant non-alignment) of other parts with the accompaniment, and the presence of ornamental techniques such as flams which enrich the musical texture but also complicate the rhythmic analysis.(3) A difference between two distinct rhythmic categories (Long vs. Short) and a periodic pattern (Long Short Short) is visible to the eye in the bottom part. Henceforth these patterns will be abbreviated with “L” and “S”, e.g., “L-S-S”. For an impression of the absolute durations concerned, we add the measured inter-onset intervals (IOIs, in milliseconds) at the very bottom.
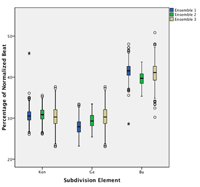
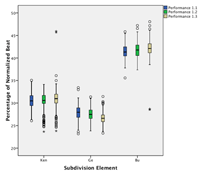
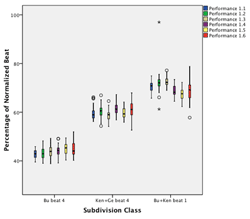
[18] The performance of both Ngòn and Bire involves large-scale tempo acceleration (see Table 2.2). The raw IOIs could thus not be used for analysis of subdivision over the course of a piece. Subdivision durations are therefore given as proportions of their local beat duration, effectively normalizing subdivision structure for tempo.(4) For instance, an isochronous binary subdivision would be described as a 50:50 ratio (each of the two subdivision elements takes 50% of the beat duration); a L-S rhythm (trochee), when based on an isochronous ternary subdivision, is described as a 67:33 ratio; a L-S-S rhythm (dactyl) which is based on an isochronous quaternary subdivision is described as 50:25:25; and so forth. Where appropriate, absolute timing values (in milliseconds) will be employed for description and/or analysis.
[19] The performances we analyze represent total social and artistic facts, many aspects of which are not documented in the audio recordings. Moreover, even the audio recordings feature many important aspects we do not take into consideration. Some of these––such as timbre sequences, ornamental embellishment, agogic phrasing, or motional patterns––would represent important aspects of a more holistic understanding of the musical structure and expression. We nonetheless focus on the structure of the beat subdivision, and periodic patterns of non-isochronous beat subdivision in particular. We share the assumption that these subdivision patterns make a strong imprint on the dense rhythmic surfaces of Mande drumming and many other styles of beat-based music for dance, marching, or work. We further assume that they make a dominant contribution to the music’s rhythmic character, its capacity for affording entrainment, and its stylistic and/or repertoire-specific identity. Our primary argument, however, is that subdivision patterns are an integral and foundational part of a metric system, as we aim to demonstrate and discuss in this article.
Section 3: Drum orchestras, ensemble parts, and polyrhythms
[20] The polyrhythmic texture of the drum ensemble music in the current study typically consists of three functional parts: the basic metrical accompaniment, the repertoire-determinative “hook,” and the improvising and regulative lead drum. This section introduces the Bamana and Khasonka drum ensembles and then gives a concise explanation (with video examples) of each of the parts for the two pieces we study.
3.1 The drum orchestras
[21] Bamana drum ensembles in the region of Segu feature three instruments. The bòn is a cyclindrical, sometimes slightly conical wooden drum. It has one goatskin membrane of about 30 cm in diameter sewn on and tightly fastened with lacings. Drummers produce a sharp high-pitched sound with a very thin and slightly flexible rod stick in the right hand and a deeper and more resonant sound with the bare left hand. The cunba is a huge wooden kettle drum. Played with bare hands, its cowhide membrane produces a roaring bass. The Kirango youth association’s 25-kg-specimen is about 50 cm high and more than 60 cm in diameter. Its membrane is fastened with metal clamps, straps, and screws. The cylindrical ngangan has two goatskin membranes of 25–30 cm in diameter sewn on to its light wooden body. Leather strap lacings connect the drumheads. Beating the batter head with a light stick produces a trenchant sound of medium pitch; the other head is just for resonance. A typical ensemble consists of two bòn, one cunba, and one ngangan. The first bòn improvises the lead part, while the second one serves as accompaniment. The cunba’s and ngangan’s patterns interlock to create the hook theme.
[22] Khasonka drum ensembles can comprise a variety of instruments, yet the core instrument is the dundunba, a double-headed cylindrical drum with goatskin membranes. The instruments are about 33–37 cm in diameter and 55–70 cm long. The player hits the drum with a curved wooden stick in his stronger hand,(5) and at the same time hits a bell fixed to his weaker hand’s index and middle fingers with a strong iron nut or ring slipped on his thumb. Typically, one dundunba plays the lead part, while a second one is responsible for providing accompaniment in the bell and a catchy hook line on the drum.
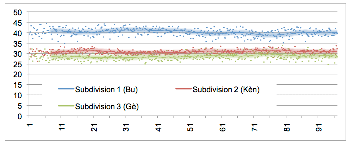
3.2 Accompaniment
[23] The drumming patterns of the accompaniment part tend to be short, simple, and dense. They are only one or two beats long, in contrast to the typical four- or eight-beat spans of hook and lead phrases. Their timbre-melodic and rhythmic outline is simple, and it is typically is performed strictly ostinato throughout whole pieces. The accompaniment rhythms typically articulate most, if not all, of the available metric subdivision elements and thus contribute greatly to the ensemble texture’s overall density. They thus make the structure of subdivision audible and salient as the surface texture or metric “feel” of the ensemble rhythm.
[24] Accompaniment motives are usually performed on the same type of instrument that plays the lead part. In Segu Bamana drumming it is the second bòn, and in Khasonka dundunba music it is the second dundunba player’s bell.(6) In the following, we briefly describe two typical accompaniment patterns, which refer to our sample pieces, Ngòn and Bire.
Kèngèbu: bòn accompaniment in Segu Bamana drumming
Video 3.1. Kèngèbu accompaniment
(click to watch video)
Figure 3.1. Kèngèbu accompaniment of the second bòn in Segu Bamana drumming
(click to enlarge)
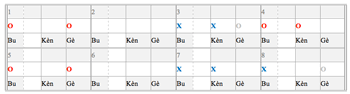
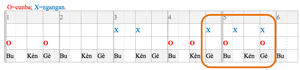
[25] If accompaniment stands out among ensemble parts as a marker of the metric beat, then Segu Bamana drumming stands out among Mande drumming styles by its doggedly consistent realization of accompaniment. In all pieces of this stylistic tradition’s repertoire, the second bòn performs one and the same motive. Its rhythm and melody is very simple: it has three strokes of two timbral qualities which span one beat’s duration. The rhythm is L-S-S, the melody is low-high-high. The high notes are played with a thin stick and the low one with the bare hand. Locals call this motive “kèngèbu,” with “Kèn” and “Gè” onomatopoetically representing the high short notes, and “Bu” standing for the low long one. The kèngèbu syllabification indicates that enculturated listeners tend to hear the grouping as anacrustic, starting with the two short notes on the offbeats. Accordingly, performers as a rule use the first of the two offbeat notes as their point of entry. The anacrusis and forward motion of the short motive, which ends on each onbeat, create a strong sense of the beat (see Video 3.1 and Figure 3.1).
[26] The Time-Unit-Box notation used in Figure 3.1 and below has been adapted to the metrical system of Mande drumming. The vertical lines mark the metric cycle (double line), beat (single lines) and subdivision (light grey lines). Dashed light grey lines mark latent subdivisions, as will be discussed below, whereas the solid light grey lines mark the subdivision as consistently manifest in the ensemble rhythm. The box widths distinguished by the solid light grey lines mark different categories of subdivision (Shorts and Longs). The position of each kèngèbu figure in the metric cycle is noted here for consistency; it will become more relevant in discussions of hook and lead figures below.
The bell: accompaniment in the Khasonka dundunba music piece Bire
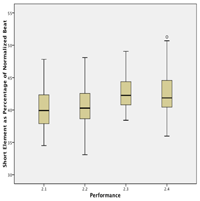
Figure 3.2. Bell accompaniment of the second dundunba for the Khasonka piece Bire
(click to enlarge)
[27] In Khasonka dundunba music, the accompaniment pattern is performed by the second dundunba player’s bell. Since the bell does not produce different pitches nor timbral variation, its motive does not contain a “melody” as does the kèngèbu pattern. The dundunba piece Bire features an archetypical two-stroke L-S rhythm in the second bell (see Figure 3.2).
[28] The rhythmic figure of the bell accompaniment is also anacrustic; players mostly use the upbeat stroke as an entry to the motive. The L-S rhythm pushes forward and lands on every beat, affording a sense of groove or beat entrainment similar to the L-S-S rhythm in the kèngèbu accompaniment for Ngòn.
3.3 Hook
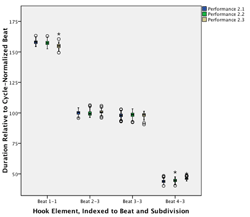
[29] While the accompaniment defines the beat and subdivisions within it, the hook’s time span marks the metric cycle as a whole. In most pieces, these are four or eight beats in length. The function of the hook part in Mande drumming is to be catchy, memorable and characteristic of a particular piece. Hook themes and timeline patterns from coastal West Africa or the Carribean share aspects of rhythmic structure, such as the tendencies for modest density (compared with the accompaniment), asymmetric accent structure, and a maximally even distribution of attacks over the metric cycle (see Toussaint 2013). However, whereas timeline bell patterns from Ghana and clave rhythms from Cuba, for instance, usually do not allow for variation and are not marked melodically, Mande hook lines mostly involve two-tone melodies and also allow for significant variation. Accompaniment motives are usually shared by some or many pieces in a repertoire, and the majority of lead-drum motives, phrases, and themes are also shared across clusters of structurally similar pieces. By contrast, the hook part does not occur in any other piece of the same stylistic tradition in a given context, time, and place.(7) When you want to unambiguously identify a certain piece, you simply sing out the hookline.
Cunba and ngangan: composite hook part in Ngòn
[30] Usually, only one instrument fulfills the hook function in Mande drumming. It can, however, be divided between two instruments in some styles. In Segu Bamana drumming, the hook is typically played by the cunba (bass drum) and complemented by the high-pitched ngangan, which plays in direct response to the cunba. Together, they create a two-tone melody, which as a unit is comparable to the dundunba’s two-tone melodies that represent the hook part in Khasonka drumming. A second aspect of the hook part’s relative complexity in Bamana drumming is the variation of motives by the cunba and, to a lesser extent, also by the ngangan.
Figure 3.3. Composite hook theme for Ngòn
(click to enlarge)
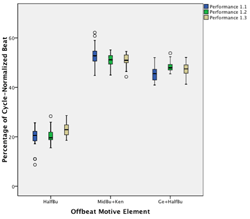
[31] For the piece Ngòn, the basic cunba motive consists of two strokes, on Beat 1 and right before Beat 2. This motive consistently repeats in each four-beat cycle and is regularly varied by two further strokes on Beat 4 (Figure 3.3). These strokes in Beat 4 function as an extended anacrusis to the following downbeat. Thus emerges a thematic phrase that implies an eight-beat metric cycle composed of two four-beat sub-cycles. The phrase has a clear beginning on Beat 1 (the downbeat of the first sub-cycle) after the long rest during Beats 6 and 7 (in the second half-cycle).
[32] The basic ngangan theme directly relates to the cunba’s. It consists of a two-stroke motive (beat-upbeat) in the first half-cycle and a three stroke motive (beat-upbeat-beat) in the second half-cycle, each of which responds to the immediately foregoing cunba motive. The result is a unified hook melody emerging from the two instruments, which reinforces and intensifies, in terms of density and melodic articulation, the cunba’s thematic structure and metric cycle.
[33] Habitual variations of the cunba fill the first half of the eight-beat metric cycle, yet carefully leave the four strokes in Beats 4 and 5 and the long rest in the second half-cycle untouched (see Video 3.2). The eight-beat cycle thus remains stable throughout.
| Video 3.2a. Trio drum ensemble performance of Ngòn (click to watch) |
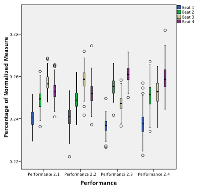
Video 3.2b. Video 3.2a, with clicktrack (click to watch) |
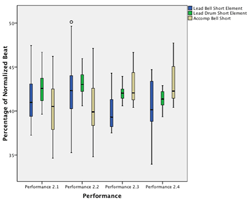
[34] Much of the corresponding song and dance supports the drum ensemble’s eight-beat meter. The basic movement pattern of the dancers, for instance, consists of a four-beat motive with each beat marked with a footstep. This motive is carried out alternately to the dancer’s right and left sides and thus constitutes an eight-beat move. The alternation is effected by a double step or, in the faster and hotter final section of the piece, a jump on Beat 4, which introduces a flip to the otherwise regular left-right sequence of footsteps (see Figure 3.4; see Video 3.3).
Figure 3.4. Basic eight-beat footstep pattern for dancing Ngòn (R=right, L=left) in phase with the eight-beat cycle emerging from the hook theme (click to enlarge) | Video 3.3. Basic eight-beat footstep pattern for dancing Ngon (slow motion) (click to watch) |
The dundunba hook theme in Bire
Figure 3.5. Second dundunba hook phrase and bell accompaniment in Bire
(click to enlarge)
[35] In Khasonka drum ensemble music, the second dundunba typically performs the hook part without change or variation. The phrase for the piece Bire is simple, short, and of little density when compared, for instance, with the hook part of Ngòn. It begins with an open stroke on the offbeat of Beat 2, followed by a closed stroke on the offbeat of Beat 3. The motive then ends with two open strokes, the first of which falls on the next offbeat (Beat 4) leading to the final stroke on the downbeat of the next cycle (Figure 3.5).
[36] The short series of anacrustic strokes builds considerable momentum, which then gives a strong sense of arrival and conclusion to the stroke on the downbeat.(8) The periodic phrase structure thus is lucent and breathing, with a clear beginning and ending; a strong expectation for the next beginning emerges during the rest after the ending (see Video 3.4).
Video 3.4a. Dundunba hook and accompaniment bell theme in the piece Bire (click to watch) | Video 3.4b. Video 3.4a, with clicktrack (polak-london_example_info.php) |
3.4 Lead
[37] The lead part is the most musically complex and prominent part in the ensemble. It is rich in motives and phrases, and has some amount of liberty for the spontaneous choice, variation, and sequential arrangement of its materials. Its main function is to coordinate the combined performance of drumming, song, speech, dance, and theatrical elements, and to mediate individual contributions—dance, in particular—to the audience. A skilled lead drummer carefully controls the “heat” of the event, most especially the gradual accelerando that is characteristic of these pieces, by manipulating musical parameters such as local rubato, loudness, rhythmic density, and the rhythmic interest that derives from multipart relationships and rhythm-meter relations. In so doing, the lead part in an improvisatory process shapes the musical form of the piece being performed.
The lead part for Ngòn
Figure 3.6. Basic lead part phrase for Ngòn; offbeat cell in red, and response cell in in blue
(click to enlarge)
[38] The most characteristic theme of the lead drum for Ngòn is composed of two alternating motives, both of which consist of three strokes (mostly flams) in their most basic variants. The first cell involves an articulation in the middle of the Bu element on Beats 1 and 2, with a middle stroke on Gè; we call this the “offbeat” cell because none of its strokes falls on a beat. By contrast, the second cell articulates the onset of Bu on Beats 3 and 4, with a middle stroke on Kèn; we call this the “response” cell since it appears as a response to, and closure of, the offbeat cell (see Figure 3.6; see Video 3.5).
Video 3.5a. Basic lead part phrase (first bòn: left) with kèngèbu accompaniment (second bòn: right) (click to watch) | Video 3.5b. Video 3.5a, with clicktrack (click to watch) |
Video 3.6. Quartet drum ensemble performance of Ngòn (Recording 1.1 of our sample)
(click to watch)
Figure 3.7. Basic L-S swing theme of the lead part (first dundunba) for Bire
(click to enlarge)
Figure 3.8. Compound ensemble melody of the basic duplet theme for Bire
(click to enlarge)
[39] The offbeat motive creates considerable polyrhythmic and metric interest by putting loud and salient strokes on time-points which are not audibly present in the accompaniment and basic hook parts, during the accompaniment’s long elements (Bu); thus, it manifestly introduces a fourth element of beat subdivision to the ensemble rhythm. Video 3.6 features a skilled quartet ensemble’s studio recording. The very basic phrase occurs twice in this recording, at 0:28–0:33 and again at 1:07–1:12. Thematic extensions and variations of the basic phrase occur frequently throughout the performance, for instance at 1:21–1:29 and at 1:39–1:53.
The lead part for Bire
[40] The lead drum’s most prominent pattern for Bire is a five- or six-stroke motive that starts in the offbeat of Beat 3, continues through the subsequent downbeat, and terminates on Beat 2 of the next cycle in the six-stroke version; the last stroke is omitted in the five-stroke variation. As a rule, the six-stroke motive and its five-stroke variation alternate and thus create a two-part theme that stretches over two four-beat cycles. This comes along with a consistent L-S rhythm in the lead player’s bell, identical to the accompaniment bell performed by second dundunba player (see Figure 3.7). We call this the “Long Short swing” theme.
[41] The accompaniment and the lead drum open tones together comprise a simple two-tone melody, which shows a balance of offbeat and onbeat accentuation (see Figure 3.8). The compound drum rhythm is perfectly aligned to the L-S swing feel afforded by both bell parts (see Video 3.7).
Video 3.7a. L-S swing theme for Bire (click to watch) | Video 3.7b. Video 3.7a, with clicktrack (click to watch) |
Video 3.8. Duet drum ensemble performance of Bire
(click to enlarge)
Figure 3.9. Opening phrase of the lead part (first dundunba) for Bire
(click to enlarge)
[42] Video 3.8 features a skilled demonstration of the basic motives, phrases, and themes for Bire. Variations of the basic swing theme fill over a third of the playing time. Melodic and rhythmic variations of that theme abound throughout (for instance at 0:22–0:32, 0:43–0:56, and 1:17–1:25).
[43] Beyond motives that remain loyal to the accompaniment bell’s L-S swing rhythm, the lead drummer frequently plays rhythmic figures that feature three subdivisions per beat, analogous to the quarternary embellishments of the lead drum in Ngòn. In our recordings, such rhythms fill more than half of the playing time. For instance, it is typical for the lead drummer to open a Bire performance with playing three successive strokes per beat in the bell and a pair of drum strokes on the first and second of the three bell strokes, with a dynamic accent on the second drum stroke (see Figure 3.9 and Video 3.9). This pattern would typically be played for a few cycles, and then, after an intermittent break phrase, the lead drum would shift to the swing theme. Three out of four of our Bire recordings employ this opening.
Video 3.9a. Opening phrase for Bire (click to watch) | Video 3.9b. Video 3.9a, with clicktrack (click to watch) |
Section 4: The timing of accompaniment motives
[44] This section discusses the timing of the two accompaniment rhythms introduced above: the L-S-S kèngèbu and the L-S bell duplet. For listeners, including audiences and performers, as well as for ethnomusicologists and music theorists, their solid regularity, high density, and melodic and rhythmic simplicity serve to convey their metric significance. Accompaniment makes the structure of the metric subdivision audible and salient, from the listener’s perspective, as the fine-grained framework for the ensemble’s polyrhythm. From the point of view of timing analysis, the accompaniment is a privileged object of study, because it makes the subdivision timings clearly apparent and hence available for chronometric measurement. This allows for studying the structure of subdivision with great reliability; understanding its degrees of stability, precision, and variation; and testing its possible correlations with, for instance, tempo or individual musicians’ playing styles.
4.1 Kèngèbu L-S-S timing in Ngòn
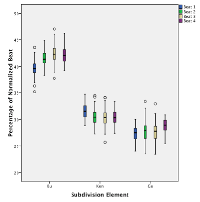
Figure 4.1. Boxplot of the grand average for beat timing (as percentage of the local cycle duration) based on the accompaniment parts in all six performances of Ngòn
(click to enlarge)
[45] The average timing for each beat in the four-beat cycle, based on data aggregated from all six performances of Ngòn, ranges between .249 and .252 (std dev. = .0056).(9) This is to say that the beat in the kèngèbu part is not just approximately isochronous, but near perfectly so. As can be seen in the boxplot in Figure 4.1, there is a slight degree of lengthening of Beat 4, and given the size of the data set the differences between all four beats are statistically significant.(10) But in absolute terms these lengthenings were typically on the order of 3–10 ms, and thus below a perceptual threshold.
[46] The subdivision, by contrast, clearly shows a non-isochronous timing pattern. The grand average of the kèngèbu pattern from all six performances is 41:31:28 (40.8—30.7—28.5) (see Figure 4.2—again, the differences between them are statistically significant).(11) This average lies evenly between 1:1:1 (perfect triplet) and 2:1:1 (perfect quadruplet) ratios. In terms of absolute duration, Bu ranges from 408 to 163 ms, while Kèn and Gè range between 307 to 114 ms, showing an effect of the 100 ms limit for the shortest elements in a rhythmic figure (London 2012, 28–38).
| Figure 4.2. Boxplot of the grand average timing ratio for the kèngèbu accompaniment pattern (click to enlarge) | Figure 4.3. Boxplot of kèngèbu timing profiles by ensemble (click to enlarge) | Figure 4.4. Boxplot of kèngèbu timings in the three performances by Ensemble 1 (click to enlarge) |
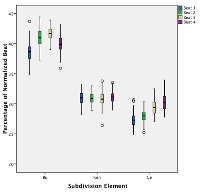
[47] Figure 4.3 shows the differences in the kèngèbu pattern as performed by the three different ensembles; all of these differences are statistically significant.(12) As can be seen, Ensemble 3 shows the greatest variability, just as would be expected in a student/novice performance. Ensemble 1 makes a greater distinction between the Kèn and Gè syllables than does Ensemble 2, and Ensemble 1 lengthens the Bu syllable more than Ensemble 2.(13)
[48] Figure 4.4 drills down a bit further, showing the kèngèbu pattern amongst the three performances of Ensemble 1. Bu is not significantly different between Performances 1.1 and 1.2, Kèn is not significantly different in Performances 1.1 and 1.3, but Gè is significantly different in all three performances.(14) These differences may be related to the different tempi in each performance. More broadly, the differentiation between Kèn and Gè that distinguishes Ensemble 1’s performances from Ensemble 2 is preserved in all three of Ensemble 1’s performances.
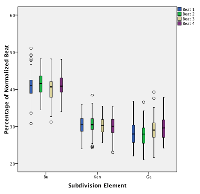
[49] The differences in the precise timings of kèngèbu by each ensemble are also affected by the slight differences in beat timing within each metric cycle. A multivariate ANOVA found significant interactions for Beat X Performance for each subdivision element.(15) These differences are clear in Figures 4.5a–4.5c. As can be seen, most of the timing variability is in the Bu and Gè elements; the Kèn timings are remarkably stable. Ensemble 1 differs from Ensemble 2 in the latter’s progressive lengthening of Gè over the course of the four-beat cycle. As Figure 4.5c shows, the student performers (Ensemble 3) make little differentiation amongst the beats in the metric cycle, other than a slight lengthening of the final Gè; in other words, they have less of a sense of phrase.
| Figure 4.5a. Boxplot of kèngèbu X Beat in Performance 1.1 (Ensemble 1) (click to enlarge) | Figure 4.5b. Boxplot of kèngèbu X Beat in Performance 1.4 (Ensemble 2) (click to enlarge) | Figure 4.5c. Boxplot of kèngèbu X Beat in Performance 1.6 (Ensemble 3) (click to enlarge) |
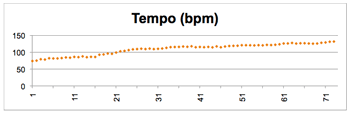
Figure 4.6a. Tempo curve in Performance 1.1
(click to enlarge)
Figure 4.6b. Timing ratio change over the course of Performance 1.1
(click to enlarge)
[50] As noted above, Mande drum pieces typically involve a structural acceleration, and Ngòn is no exception. This large-scale tempo change also affects the timing of kèngèbu, especially as different ensembles employ both different tempo ranges (starting and/or ending slower or faster) and different rates of tempo change. Figure 4.6a gives the tempo curve for Performance 1.1, while Figure 4.6b is a time-series plot of the corresponding changes in the kèngèbu ratio. The convergence between Kèn and Gè is clearly evident, and paired T-tests comparing Kèn and Gè at the beginning versus ending of the performance (i.e., first vs. last 50 beats) were highly significant at the beginning (t(49) = 20.76, p < .001) but only nearly significant at the end (t(49) = 1.92, p = .058). For Performance 1.2 the convergence was even greater, as the difference between Kèn and Gè becomes non-significant (t(49) = .491, p = .861).(16) Contrast this with the analogous Figures 4.7a and 4.7b, which correspond to Performance 1.4. There the Kèn and Gè syllables do not converge, though there is an interesting shift in their correlation (beginning: t(49) = 14.05, p < .001; ending: t(49) = -2.404, p = .020); rather, they are very close to each other from the outset.
Figure 4.7a. Tempo curve in Performance 1.4 (click to watch) | Figure 4.7b. Timing ratio change over the course of Performance 1.4 (click to watch) |
[51] In summary, the kèngèbu accompaniment in Ngòn involves a non-isochronous L-S-S subdivision, with an average timing ratio of 41:31:28 (40.8—30.7—28.5), though it should be noted this grand average obscures the distinctive timing patterns of each ensemble. These elements are subject to expressive timing nuances, which, while small in size, are characteristic of particular performers and/or ensembles. There is a reduction in size of expressive nuances within the “Short” category. While also affected by tempo, the essential distinction between the Long and Short elements remains clear throughout all six performances.
[52] Two additional aspects of kèngèbu deserve comment. First, the timing pattern’s structure and ratio turn out to be independent from the performance context. Performance 1.1 isolated the drum ensemble whereas Recordings 1.2 and 1.3 involved singers and dancers as well, yet the basic timing proportions and expressive nuances remained much the same throughout. Second, the pattern’s structure and ratio is not dependent from the performing musicians experience or expertise. An ensemble of novice youth drummers, singers, and dancers (Ensemble 3, Performance 1.6, ages 15–16) performs the same basic timing pattern, albeit with somewhat less precision, or somewhat greater variability.
[53] With kèngèbu we thus have a meter that is non-isochronous on its foundational layer, i.e., its subdivision. Despite this strong non-isochrony—the long pulse being distinctly longer than the short ones—the pithiness, short periodicity, and great stability of that L-S-S pattern still creates a sense of regularity, holding together the parallel and subsequent elements of a complex rhythmic flow.
4.2 Bell accompaniment timing in Bire
Figure 4.8. Boxplot of Beat Duration (relative to 4-beat cycle) X Performance for Bire
(click to enlarge)
Figure 4.9. Boxplot of Short element of the L-S accompaniment figure in Bire
(click to enlarge)
[54] As in Ngòn, Bire involves non-isochronous subdivisions of an isochronous beat. In Bire, however, there is greater variability in beat length, as the average beat length (normalized by cycle) from all performances is .239—.251—.255—.256. Figure 4.8 shows the highly significant pattern of beat length in each of the four performances of Bire under analysis.(17)
[55] As can be seen in Figure 4.8, there are similarities between Performances 2.1 and 2.2 (Koly Sacko on accompaniment) and Performances 2.3 and 2.4 (Toutou Sacko on accompaniment). Performances 2.1 and 2.3 are duos, while Performances 2.2 and 2.4 are trios (with an added jembe part). As is evident, the additional drum did not affect the basic beat timing pattern of each ensemble. Finally, it is worth remembering here (and below) that the Bire accompaniment and hook are played by one and the same player, with the bell played in the left hand and the drum by the right. Typically, the musician focuses on playing the drum with his strong hand and lets the bell in his weak hand just come along unconsciously. The greater variability and reduced tempo ranges that we observe in Bire may be related to the higher task demands involved in a bimanual, multi-part rhythm production.
[56] The grand average ratio for the L-S figure in the accompaniment bell in our four recordings is 59:41 (58.6—41.4). Figure 4.9 plots the Short element for each performance (Long elements are omitted as they are redundant), and makes clear that the different players have slightly different swing ratios when playing the accompaniment part.(18)
[57] Independent samples T-tests comparing the two performances by each player were significant for Koly Sacko (performances 2.1 and 2.2; t(1054) = -2.80, p = .005) but not for Toutou Sacko (performances 2.3 and 2.4; t(826) = .523, p = .601). When broken down by performer, we see that Koly Sacko’s L-S ratio is about 60:40 (59.55—40.45), while Toutou Sacko’s ratio is about 57:43 (57.4—42.6). Thus each performer has a characteristic personal style of expressive timing, relative to both the four-beat cycle and to the L-S beat subdivision.
Figure 4.10a. Time-series plot of the accompaniment ratio in Performance 2.1
(click to enlarge)
Figure 4.10b. Time-series plot of the accompaniment ratio in Performance 2.3
(click to enlarge)
Figure 4.11. Scatterplot of bell vs. jembe timings in Performances 2.3 and 2.4; comparisons are made between corresponding IOIs rather than beat-normalized ratios
(click to enlarge)
[58] In Performance 2.1 (Video 3.8), over the course of the three-minute piece the tempo accelerates from about 85 bpm to 125 bpm. The mean timing ratio changes from 59:41 in the beginning of the piece to 61:39 in the end (from 59.3—40.7 to 60.5—39.5; see Figure 4.10a). A related samples T-test on the beginning versus final 100 beats shows that the difference is subtle but statistically significant (t(99) = 3.27, p = .001). In Performance 2.3 (see Figure 4.10b), however, there is little change in the bell ratio (i.e., the Short element shifts from 42.8 to 42.5; this difference is not statistically significant).
[59] The metric feel created by the non-isochronous subdivision is nearly independent of tempo; in other words, the two subdivision categories (Long vs. Short) are stable under tempo change.
[60] As with the L-S-S (kèngèbu) pattern in Ngòn, the expressive timing differences detailed above (between performers, performances, and tempo ranges) do not change the essential character of the L-S (bell) accompaniment rhythm in Bire.
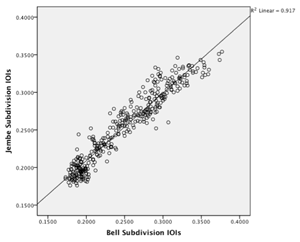
[61] Bire Performances 2.3 and 2.4 of our sample include a third drum, a jembe accompaniment (slap—tone-slap—bass), the rhythm of which (x.xx.x) parallels the bell accompaniment. The grand average of the subdivision ratio for the jembe accompaniment in the two recordings is 59:41 (58.65—41.35); recall that the grand average for the bell timings, too, is 59:41 (58.6—41.4). Figure 4.11 is a scatterplot, which shows the tight linkage between the bell and the jembe. A Pearson product-moment correlation between the two is both strong (R(370) = .958) and highly significant (p < .001). Thus when an accompanying jembe drum is added, it follows the subdivision timing established by the bell.
[62] To summarize, accompaniment for Bire is marked by an L-S rhythm that is performed with a stable timing ratio in each recording. A particular range of ratios (57:43–60:40) is characteristic of the piece across individual playing styles and tempos. The variation between different recordings and tempo ranges is small, but characteristic differences between performers are evident.
Section 5: The timing of hook themes
[63] This section analyzes the timing of hook parts and discusses their contribution to the ensemble rhythm, as first approached above in the example of accompaniment parts.
5.1 Cunba and ngangan basic patterns
[64] Recall that the hook part in Ngòn projects an eight-beat cycle consisting of two four-beat half cycles. While two short motives (one for each half-cycle) often make up a basic theme (see Section 3.3, Figures 3.3 and 3.4), those motives may be integrated into a more complex figure when variations are present. Moreover, there are optional anacrustic strokes which sometimes are played and sometimes not. Thus, unlike the kèngèbu ostinato in the accompaniment part, one can only perform a limited statistical analysis of the variative hook parts (cunba and ngangan) in Ngòn.
Figure 5.1. Boxplot of cunba invariant hook motive in all six performances of Ngòn
(click to enlarge)
[65] Cunba players habitually include variations that fill the first half-cycle and thus connect the theme’s two basic motives into a single grouping, yet they carefully leave untouched the four strokes in Beats 4 and 5—specifically, articulating Bu and Kèn in Beat 4 and Bu and Gè in Beat 5 (see Section 3.3, Video 3.2). This figure marks the midpoint of the eight-beat cycle, and it is the three intervals marked by these four strokes that are analyzed here. First, note that this figure articulates the onbeat position in both beats, but then different offbeat positions in each beat. As such, it will produce three distinct IOIs; expressed as percentages of the beat duration (here normalized relative to the four-beat cycle), the grand average timing ratio for all six performances is 44:60:70. As one would expect, there are expressive timing differences from performance to performance (see Figure 5.1).
[66] Again, the student ensemble (Performance 1.6) shows the greatest variability, but as is evident in the boxplot, there are significant differences amongst the performances for each syllable.(19) Most crucially, however, the “Bu” IOI takes 43–45% of the normalized beat duration in all performances, and the “Kèn + Gè” IOI is in all cases distinctly shorter than the “Bu + Kèn” IOI, showing how the non-isochronous (L-S-S) subdivision underlies the timing of this figure.
[67] The ngangan basic theme, too, confirms the subdivision timing pattern inherent in the kèngèbu accompaniment part. Its invariant beat-upbeat-beat motive in Beats 7–8 gives a mean beat-upbeat ratio for Beat 7 of 41:59 (41.3—58.7, grand average of Recordings 1.1, 1.4, and 1.5). In sum, the hook parts’ basic motives confirm the accompaniment’s L-S-S subdivision pattern and thus add to its stability and salience.
Figure 5.2. Composite hook theme for Ngòn, with ngangan offbeat variation highlighted in orange frame
(click to enlarge)
Figure 5.3. Screenshot of the audio waveform of the ngangan variation (top) and kèngèbu accompaniment (bottom) in Ngòn
(click to enlarge)
[68] A final point must be made regarding the ngangan hook part, which also leads to the following discussion of the lead drum parts. In Ngòn, ngangan players often add a variation to their basic motive, which consists of a three-stroke series of offbeats extending from Beat 4 to Beat 5. This variation of the ngangan part does not completely align with the kèngèbu accompaniment (see Figure 5.2). Figure 5.3 shows a screenshot of audio files showing the waveforms of the ngangan variation and kèngèbu motives. One can see that of the three consecutive offbeat strokes that extend across Beat 5, the first and the third one align almost perfectly with the Gè (the second “S” of L-S-S) in the kèngèbu accompaniment, whereas the medial one (immediately following Beat 5) does not align with any stroke in the accompaniment but further subdivides the Bu (“L” of L-S-S).
[69] The ngangan variant noted above only appears intermittently in each performance, and where it does occur, the overt division of the “L” element of the basic L-S-S kèngèbu pattern takes place only once within the eight-beat cycle. Therefore, chronometric and statistical analyses were not performed due to limited sample size. A similar variant in the lead drum part, which articulates this same position here and elsewhere in the eight-beat cycle, is analyzed below.
5.2 The second dundunba’s timing in Bire
Table 5.2. Bire hook theme performance timing (in percent of the beat duration [normalized by cycle])
(click to enlarge)
Figure 5.4. Boxplot of the timings of the dundunba hook part in three performances
(click to enlarge)
[70] In Bire the second dundunba’s hook theme is an invariant ostinato (see Section 3.3, Figure 3.5, Video 3.4). Its timing is yoked to the accompaniment bell rhythm, as it is played by the same drummer with his other hand. Table 5.2 gives the grand average of the timing of the hook theme, as well as the average timings of the hook pattern in each recording (relative to the local beat cycle); Figure 5.4 shows these timings as a boxplot.
[71] As can be seen in Figure 5.4, there are slight differences in expressive timing for each hook element––except for the IOI that begins on Beat 3.3––and all were significant save for Beat 3.3.(20) Of particular importance for the rhythmic feel of the hook phrase is the pair of strokes occurring on the offbeat before and then on the downbeat (Beats 4.3 and 1.1). The IOI between these two strokes takes 44–46% of the normalized beat duration and thus is clearly expressive of the accompaniment bell’s underlying L-S swing feel.
[72] The timing data for the hook patterns in both Ngòn and Bire show their rhythmic stability and their linkage to the non-isochronous timing of their respective accompaniments. This bolsters the claim that the timing of both the accompaniment and hook parts involves a shared metrical framework that is not based on simple integer ratios, but nonetheless shows the same kinds of expressive timing and ensemble coordination behaviors we find in the context of isochronous metrical frameworks.
Section 6: The timing of lead-drum phrases
[73] This section studies the timing of a selection of basic lead-drum phrases and considers their contribution to the emerging meters. The analysis of the accompaniment and hook parts given above show that Ngòn and Bire involve stable beats, higher level beat periodicities (cycles of 2, 4, and/or 8 beats), and non-isochronous beat subdivisions. The lead drum parts both reinforce this framework and enrich it.
6.1 A lead drum phrase for Ngòn
Figure 6.1. Rhythmic figure of the lead part’s basic phrase (top) and kèngèbu accompaniment (bottom) for Ngòn
(click to enlarge)
Figure 6.2. Boxplot of the “Offbeat Motive” from lead drum, Performances 1.1–1.3
(click to enlarge)
Figure 6.3. IOIs (in grey) and running timing (bold black), both in ms, of the lead drum playing a continuous series of offbeats (two top rows) and the second bòn playing kèngèbu accompaniment (two bottom rows) in one eight-beat cycle of Performance 1.1 (Video 3.6, 1:21–1:26)
(click to enlarge)
[74] We confine our analysis of the lead drum in Ngòn to the two motivic cells—the “offbeat” and the “response” motives—that make up the basic phrase introduced above (Section 3.4, Figure 3.6, Video 3.5); Figure 6.1 shows its rhythmic structure again.
[75] The grand average timing ratio for the offbeat motive is 52:48; the onbeat motive, by contrast, is 43:57. Thus, the offbeat motive is not simply a phase-shifted version of the onbeat motive, but a re-alignment of the strokes with alternate positions within the kèngèbu accompaniment. Most crucially, it involves a consistent articulation after the onset of the Bu element. Figure 6.2 gives a boxplot of the offbeat motive in each performance. The initial “HalfBu” element is the offset of the first element in the lead drum relative to the onset of the corresponding Bu onset in the accompaniment. The boxplot shows that within and across all three performances, this motive is consistently placed at the midpoint of the Bu element of the kèngèbu pattern: the lead drum’s HalfBu offset (~20%) amounts to half of the kèngèbu’s Bu duration (~40%). Likewise, the “Gè+HalfBu” element falls at the midpoint of the next Bu in the metric cycle. Though all performed by the same drummer and ensemble, performance specific timing differences are evident and statistically significant.(21)
[76] When playing the offbeat figure repeatedly, which is a common variation of the lead drum’s basic phrase, the subdivision of the Bu element into two equal halves is evident not only in the within-beat ratios, but also in a time series analysis (see Figure 6.3). The distance of the lead drum’s first stroke in each beat from both the first (Bu) and second (Kèn) strokes of the accompaniment averages 112 ms; the average placement of the offbeat stroke is precisely at the midpoint of the Bu element’s duration (.501; Std Dev = .061). The timing data also show the close alignment of the lead drum’s second stroke in each beat with the third element (Gè) in the accompaniment.
[77] The denser subdivision, which emerges from the composite of the accompaniment and lead parts, displays an s-s-S-S pattern (Very Short—Very Short—Short—Short). “Short” and “Very Short” here represent two different categories of subdivision that are possible in the kèngèbu pattern. The two very short elements sum up to the duration that the Long (Bu) has in the original L-S-S pattern. The timing of the two short elements in the L-S-S pattern notably stays undisturbed by the further subdivision of the Long into s-s.
[78] Other motives containing strokes that subdivide Bu (the second “s” position of s-s-S-S) occur frequently in the lead drum part.(22) The denser subdivision resulting from them appears as not only a singular or local phenomenon, but as a general characteristic of lead drumming for Ngòn.
6.2 Lead drum timing in Bire
Table 6.2. Mean timing ratio (in percent of the beat duration) in the “swing duplet” lead drum phrase for Bire
(click to enlarge)
[79] The single most characteristic and most frequently played lead drum pattern for Bire is the “L-S swing” theme (see Section 3.4, Figures 3.7 and 3.8, Video 3.7). It fills about one third of the playing time in our corpus of Bire recordings. Note that the lead drummer also plays a bell pattern (which will vary, as opposed to the accompaniment bell), so that in addition to the lead drum we may observe the timings of the “lead bell,” as well as the timings of the “accompaniment bell.” These are summarized below in Table 6.2.
[80] Nuances of swing ratio are a matter of personal style. In Recordings 2.1 and 2.2 Koly Sacko plays the lead parts (bell and drum), while his brother Toutou Sacko plays the accompaniment and hook parts; in Recordings 2.3 and 2.4 their roles are reversed (note shadings in Table 6.2). Koly Sacko plays the L-S rhythm more evenly than Toutou Sacko, independently of whether in the accompaniment or lead parts.
Figure 6.4. Boxplot comparing subdivision elements in Bire lead and accompaniment parts
(click to enlarge)
Table 6.3. Grand average of timing ratios (in percentages of the beat duration) in the lead drum and bell parts which open Bire (Recordings 2.1, 2.3 and 2.4)
(click to enlarge)
Figure 6.5. Screenshot of the accompaniment (top track) and lead part (bottom track) bell strokes in the opening of Performance 2.1 (Video 3.8)
(click to enlarge)
[81] No matter who is playing the lead bell, one can see that the swing ratio is slightly more even in the lead drum than in the bell. Moreover, the lead drum rhythm generally is slightly more regular than the bell; this is easier to see in terms of the width of the lead drum boxplots (in green) versus the lead bell boxplots (in blue) in Figure 6.4.(23)
[82] Figure 6.4 also shows that overall variability is higher in Bire than in Ngòn, reflecting the greater demand of dual-instrument performance. This figure also confirms our anecdotal observation that the drum is played with the dominant hand and the bell follows––hence the much lower variability of the lead drum versus the lead bell parts.
[83] We now proceed with an analysis of the lead drummer’s opening phrase for Bire (see Section 3.4, Figure 3.9 and Video 3.9). This rhythmic figure features three subdivisions per beat, which is as characteristic of the lead part in Bire as is the binary L-S swing rhythm discussed above.
[84] The drum and bell are not perfectly aligned, and so it is difficult to locate a precise moment marking the lead drummer’s first and second onsets per beat. Nonetheless, his second bell/drum strokes clearly give a non-isochronous division of the Long of the basic L-S accompaniment (see Table 6.3).
[85] Yet, the third element of the lead drummer’s bell pattern aligns with the Short element of the accompaniment’s bell. This creates a ternary s-S-S subdivision pattern (Very Short—Short—Short) that does not change the metric identity of the second (“S”) element of the L-S accompaniment. Figure 6.5 gives a screenshot of an audio track showing the two bell parts during the opening episode.
[86] Note also that the drum plays a more uneven ratio than the bell here, whereas in the case of the swing duplet rhythm, the drum showed the more even ratio. We posit, however, that both timing patterns stem from the same motivation: the lead drummer is distancing his rhythm from an isochronous triplet feel through a strong degree of swing. To achieve this, duplet rhythms require more even ratios (for instance, 55:45), while ternary rhythms require rather uneven ratios (for instance, 22:33:45). Indeed, the lead drum’s second stroke per beat in the opening phrase is typically on the edge of flamming with the first stroke, and thus takes on a distinct quality of particular perceptual salience and quasi-ornamental appeal. We suggest that the expressive intention here is twofold: first, to put rhythmic accent on the beat, and second, to highlight the non-isochronous pattern of the beat subdivision. To put it differently, the lead drummer’s opening of Bire basically amounts to a summary of the rhythmic feel of the piece.
[87] In addition to the three-stroke opening, one performer (Toutou Sacko) will play three bell strokes per beat at other times during the performance (Recordings 2.3 and 2.4). The grand average of his timings in both performances is 25.4—35.3—40.4, almost exactly the same as in the opening.
[88] In contrast to Ngòn, where the lead drum subdivides the Bu element into two equal halves, as the grand average ratio indicates, the lead drum’s subdivision of the “L” of the L-S pattern in Bire is more complex. Like Ngòn, the “L” of L-S in Bire is subdivided into two elements. Unlike Ngòn, however, they are uneven—one Very Short and one Short element. And the Short element is close to (but distinctly shorter than) the Short element of the core L-S pattern, which already is present in the accompaniment and hook parts. Thus the pattern that emerges is s-S1-S2. The difference between “S1” and “S2” is somewhat stronger than the expressive timing differences between Kèn and Gè in the kèngèbu pattern. We nonetheless regard “S1” and “S2” as members of the same metrical category for several reasons. First, a perceptual study indicates that Malian musicians and listeners still perceive them as the same category, and do not discriminate between them as they do between “s” and “S” (Neuhoff et al., forthcoming). Second, the timing differential arises in part through the interaction between timing constraints relative to the core pattern, i.e., such that “S2” (of s-S1-S2) = “S” (of L-S), along with coordination constraints of timing the onset of S1 relative to the other parts of the musical texture. These latter constraints are of course exacerbated by the high task demands of playing both the bell and lead parts (and the concomitant increase in timing variability).
[89] We can understand these constraints as follows. In terms of timing, if the lead drummer’s task is to divide the “L” element, there are two possibilities. One may divide the “L” element equally, producing something like an s s S pattern (analogous to division of the Long in kèngèbu), which would have something like a 30:30:40 timing ratio. Alternatively, one may divide the “L” element unequally, and then produce something like S-s-S or s-S-S. The latter is what is involved in Bire, but with a twist: the goal is to make “s” distinct from “S”, but a simple s-S-S is problematic as this would produce a 20:40:40 ratio. That ratio creates two problems. The first is that the “s” in this context is only half the duration of the S, which invites a confusion of metrical levels.(24) The second and more pressing problem is that if the “s” is only 20% of the beat span, the sense of a flowing pulse-stream may get lost through too sharp a distinction between its elements, especially at faster tempos. Therefore, the solution to this timing problem is to smooth out the 20:40 ratio difference, at the same time making sure that “S1” is close enough to “S2” in order for the two to be heard as categorically similar. A normative 25:35:40 ratio achieves this most efficiently and elegantly.(25)
[90] The above analysis of the lead drum opening phrase strongly confirms our claim that the lead part’s denser ternary subdivision pattern (s-S1-S2) nests into the accompaniment and hook parts’ binary subdivision (L-S).
6.3 Summary: lead part timing in Mande drumming
[91] In both Khasonka and Bamana drumming, the lead player often makes use of two different density levels upon which to build rhythmic figures: a slower one that is established and permanently kept present by the accompaniment part, and a somewhat faster one that is manifest mainly in the lead part. Both density levels contain two (and only two) qualitatively/durationally distinct categories of subdivision elements (Long vs. Short, or Short vs. Very Short). The lead players’ timing of rhythms on the slower density level does not differ from the timing of rhythms on the same metric level in the accompaniment and hook parts. Their timing of rhythms on the faster level subdivides the initial long element of the slower level subdivision (the “L” of the L-S swing figure in Bire; and the “L” of the L-S-S, or Bu of kèngèbu accompaniment in Ngòn), but leaves the original short element(s) undisturbed. In the lead drum parts, expressive timing articulations take place in the long element and its subdivision rather than in the short element(s). This indicates that the sustained integrity of the short element(s) is of primary importance. A binary subdivision thus is hierarchically coordinated with a ternary subdivision (L-S = s-S-S); analogously, a ternary subdivision can be coordinated with a quaternary one (L-S-S = s-s-S-S).
Section 7: Conclusion
7.1 Categorical production and perception of uneven rhythms in Ngòn and Bire
[92] The accompaniment parts in Ngòn and Bire involve isochronous beats with non-isochronous yet stable subdivisions, creating L-S-S and L-S patterns (respectively) that are not related by simple integer ratios. The kèngèbu pattern in Ngòn has an average ratio of 41:31:28 (40.8—30.7—28.5), while the “swing” bell accompaniment’s average ratio in Bire is 59:41 (58.6—41.4). Given the rapid tempos of Ngòn and Bire (especially in the latter parts of each performance), these ratios cannot be based on an isochronous substrate which might underlie a simpler ratio of 4:3:3 or 3:2, as the IOIs for such pulses would simply be too short, exceeding the 100 ms limit for rhythmically salient events (for a summary of research on the 100 ms limit see London 2012; Repp 2005; Repp 2006; and Repp and Su 2013). Also, they cannot be read as expressive deviations from isochronous binary (50:50), ternary (33:33:33) or quaternary subdivisions (25:25:25:25), since such a reading would imply that Bire is either binary or ternary and Ngòn is either ternary or quaternary. This, however, would amount to an undue reduction of what these rhythms have to offer. By contrast, we will present a model of how non-isochronous subdivision does allow for the hierarchic coordination, and thus simultaneous presence of binary and ternary, or ternary and quaternary, subdivisions (see below, Section 7.3).
[93] The hook parts give further evidence of the stability of the non-isochronous beat subdivision, as the hook patterns are clearly anchored to either the Long or Short locations as defined by the accompaniment. In other words, though the hook patterns are rhythmically less continuous than the accompaniment, all the performers are clearly maintaining a common metrical framework based on the non-isochronous beat subdivisions expressed in the accompaniment parts.
[94] While the kèngèbu and swing bell accompaniments are stable, they are nonetheless subject to expressive timing variations. Different performing ensembles (for Ngòn) and performers (for Bire) showed distinct timing profiles. While these expressive variations were affected by tempo—diminishing the difference between the short elements in kèngèbu—this was not analogous to a broader assimilation tendency (i.e., where the “S” and “L” elements converge to a single value) or showing a tendency toward a 2:1 ratio, as noted by Fraisse (1963) and Povel (1981). Though to be fair, those previous studies involved a different rhythm production task, namely to continuously produce an “artificial” non-isochronous non-integer rhythm in a laboratory setting, rather than our musicians who produced vernacular rhythms in an actual performance. More recently, in an experiment inspired by Fraisse’s and Povel’s work, Repp, London, and Keller (2012) found that even 2:1 ratios were slightly distorted, and thus they posited the existence of a tempo-dependent attractor ratio somewhat less than 2:1. Indeed, the stability of the core ratios for Ngòn and Bire under continuous tempo change is most notable in our current study. Given that this acceleration is characteristic of Mande drumming performance, there may be a practice effect at work here: unlike the participants in the experimental tests cited above, whose task was to reproduce various rhythms (presented in randomized orders) at different tempos, our Malian musical colleagues had the task of presenting the “same” rhythm while under constant tempo transformation.
[95] Additional performance constraints are evident in our study beyond the flattening out of expressive nuance noted above. In Ngòn, the presence of the lead drum may limit the maximum tempo, as the fastest performances we observed involved trio presentations without a lead drum. In Bire, the task demand of each performer playing both the bell and drum (whether lead or hook) may also limit the maximum possible tempo; structural accelerandos were consistently milder in Bire than in Ngòn.
[96] Thus, the Mande drumming pieces we have studied give evidence for two distinct subdivision interval classes defined qualitatively, as a durational pattern, and not quantitatively, as comprising different numbers of equivalent sub-elements. That is, the Long and Short subdivision categories in Ngòn and Bire are not based on a duplet vs. triplet distinction, nor are theses subdivisions concomitantly based on simple integer ratios; for instance, it is not true that two Shorts can substitute for one Long, or vice-versa. Rather, a clear and characteristic durational distinction is maintained between the two. Indeed, the ratio range in which we find the L-S or L-S-S patterns of Bire and Ngòn is optimal for the production (and categorical perception) of uneven rhythms that are not based on nominally isochronous subdivision and simple integer ratios.
[97] These pieces also refine our notion of what categorical rhythm production and perception entails. Clarke (1987) gives what is perhaps the clearest explication of categorical perception in music, which is an adaptation of the notion of categorical perception in speech and vision:
Thus, for example, in the perception of musical intervals, a person will make a categorical judgement of the interval type (e.g. major third, perfect fifth, minor second, etc.), as well as a judgement of how well-tuned the interval is. The latter judgement (intonation) relies upon assessing the perceptual information left over following categorisation. (Clarke 1987, 22)
[98] Clarke then hypothesized that, for rhythm, categories may be based on small integer ratios, following the experimental studies and theories of Fraisse. Clarke found evidence of categorical perception of metrical subdivision by presenting subjects with incremental changes of a figure (i.e., from an even to uneven subdivision, or vice-versa), primed by either an isochronous duplet or triplet context. As hypothesized, the priming context was retained until there was an abrupt shift from a perception of evenness to unevenness (or vice-versa). This led Clarke to conclude:
1. When listening to music that belongs to a metrical tradition, we perceive duration relations between notes as belonging to two basic classes: even and uneven divisions of a metrical timespan. The position of the categorical boundary between these two classes is dependent upon the metrical context, so as to favour metrically conformant interpretations of ambiguous rhythmic structures.
2. Truly categorical distinctions appear not to exist within the class of uneven timespan divisions. Rather we perceive different uneven rhythms, such as [quarter—8th in compound time] and [dotted 8th—16th in simple time] as lying at different points on a continuum rather than as distinct types. A particular uneven rhythm on this continuum may be fixed by a coordination of the uneven class with a metrical class—of which there are two fundamental types in the majority of Western music: duple and triple. Thus [quarter—8th] is a coordination of uneven with triple, and [dotted 8th—16th] a coordination of uneven with duple. (Clarke 1987, 30)
[99] We accept conclusion one but reject conclusion two. Or rather, we modify conclusion two and suggest that in contexts such as Mande drumming, a third category may appear—one that is not based on a duplet or triplet and not on a small integer ratio at all, but rather on a non-integer L-S relationship. Moreover, this non-isochronous ratio may then serve as the framework for further metric elaboration, albeit in a highly restricted fashion (i.e., where L-S morphs into s-S-S in the case of Bire or where L-S-S morphs into s-s-S-S in the case of Ngòn). Clarke (2000) acknowledges the effect of context on the formation of categories, and thus the evidence we have presented gives support to his later view. As Clarke notes, categorical perception involves the distinction between within-category distinctions (different shades of blue; more or less in tune pitches) versus between-category judgments (blue versus green; the pitch class B versus the pitch class
[100] The presence of a “tertium quid” (i.e., an uneven rhythm that is neither a variant of a 1:1 nor a 2:1 ratio) also reminds one of the lure and bias of musical notation: while one may capture categorical distinctions with a notational orthography based on simple integer ratios, this does not mean those categories necessarily or inherently involve simple integer ratios. As Bengtsson (1974) noted in his pioneering empirical studies of rhythm in actual performance, one must understand “notation as a character- and symbol-system that includes explicit and implicit reading rules and interpretive norms” (Bengtsson 1974, 200; our translation from the German “Notation als Zeichen- und Symbolsystem einschließlich expliziter und impliziter Leseregeln und Interpretationsnormen”).
7.2 Non-isochronous rhythms in other pieces and styles
[101] Uneven fast pulsations also appear elsewhere, particularly in Africa and the African-American diaspora. The findings on Bamana and Khasonka drumming summarized above were confirmed by further timing analyses of jembe drum ensemble music from Bamako, the Malian capital, which integrates repertoires of various Mande-speaking ethnic-regional groups, such as Maninka, Wasulunka, Bamana, and Khasonka, among others. The L-S-S subdivision pattern in the accompaniment and hook parts for the jembe piece Sunun turned out to be similar to the one for Ngòn, and the L-S timing in the jembe piece Manjanin is similar to the one in Bire (see Polak 2010). The further subdivision of the Long is present in the jembe pieces as well. We conclude that non-isochronous subdivision and its potential for further bifurcation represent common characteristics of Mande dance drumming from Mali and neighboring countries.
[102] In the Maghrib, various styles of music share with Mande drumming the characteristics of continuous tempo acceleration and prototypical accompaniment patterns based on non-isochronous subdivision, such as L-S-S. Exemplary cases include dance drumming in the context of communal celebrations of Berber peoples in southern Morocco (Olsen 1994) and music for trance rituals associated with West-African diasporic communities in Morocco (Gnawa) and Tunisia (Stambeli). In the Tunisian case, the accompaniment patterns are particularly elastic: strongly uneven ratios of L-S-S and L-S-S-L accompaniment patterns in the beginning of pieces tend to gradually flatten out with increasing tempo (Jankowsky 2010, 115–23; 2013). In Moroccan Berber music, the typical transformation of a 4/4 into a 7/8 drumming rhythm (Lortat-Jacob and Jouad 1979-LP; Lortat-Jacob 1980, 120–24; Olsen 1994-CD, track 4) also involves non-isochronous subdivisions.
[103] In samba drumming from Bahia in north-eastern Brazil, the fast pulsation of four subdivisions per beat (in a four-beat metric cycle) shows a definite and regionally specific timing pattern: medium short medium long, often with ratios of about 25:20:25:30 (Gerischer 2003, 180–99), which local musicians identify as their rhythmic dialect. Ethnomusicologist Christiane Gerischer claims these non-isochronous subdivision patterns underlie various styles of samba in Bahia and transcend the various rhythms of the ensembles’ individual parts (Gerischer 2003, 199). Her conception of the subdivision timing pattern as metric, which we endorse, is different from the still common sense view of these patterns as expressive variations of, or deviations from, a (nominally) isochronous density referent (see, for instance, Naveda et al. 2011). Gerischer also notes that the core beat-marking rhythms (x..x) can sometimes tend towards a triplet feel (x.x) (Gerischer 2006, 109–10). When the timing of the fast pulse tends towards L-S-S-L, the four subdivision elements also can form a rhythm that resembles a 6/8 feel (x.xxx.). Comparable subdivision patterns also exist in other Brazilian forms of music for marching and dancing, such as maracatu.
[104] In the study of rhythmic timing in jazz, the swing ratio has been a central concern, and we submit that this ratio is another instance of non-isochronous beat subdivision. Gridley (1985) notes that the swing ratio falls somewhere between 1:1 and 2:1 (in percentage terms, 50:50 and 67:33). Ellis (1991) in a study of saxophone improvisations found a swing ratio of 1.7—1 (63:37). Collier and Collier (2002), in a thorough analysis of swing timing in two Louis Armstrong solos, found swing ratios of 1.61—1 and 1.58—1 (around 61:39), albeit at fairly rapid tempos of 173 and 186 bpm. By contrast, Benadon’s (2006) study of excerpts performed by a variety of prominent jazz soloists found the swing ratio to range between 1.4—1 and 1.2—1 (58:42–55:45). The Colliers (2002) also found that when Armstrong played a series of offbeat/syncopated notes, he aligned them not with isochronous subdivision, but with the “swung” timing he had previously established; this is reminiscent of the alignment of the hook and lead parts with the accompaniment in Ngòn and Bire. It shows that non-isochronous subdivision can be metric in the sense of an internal pulse underlying the timing of notes in relation to even unsounded beats. Friberg and Sundstrom (2002), in their study of ride cymbal timings by a number of famous drummers (Adam Nussbaum, Tony Williams, Jack DeJohnette, Jeff Watts), found that the swing ratio varied with tempo, and that the 2:1 ratio only appeared at certain tempi. It should be noted that they explored extremely fast tempos and thus documented a forced change in the ratio: as the short element reached a 100 ms limit, it shrank no further, wheras the long elements of the pattern then got progressively shorter as the tempo continued to increase. Nonetheless, Friberg and Sundstrom also found that swing ratios were (a) mostly non-integer, (b) characteristic of particular performers, and (c) stable within the context of a particular performance.
[105] It is noteworthy that while it is common to interpret swing in jazz as an expressive variation or deviation or discrepancy, the community of jazz experts cannot agree upon what exactly is the norm that swing is a deviation from, despite much effort and intense discourse. Although many have swing as a variation of an underlying triplet, there are eminent voices that speak against the triplet hypothesis and opt for duplets (see Benadon 2006). The fact that much, if not most, swung rhythm is notated in duplets is also telling. We suggest that this lack of consensus is because swing, like Mande, is neither a variation of triplets nor of duplets, but on a non-isochronous pulse stream of its own kind. We will argue below that this view can explain how a rhythm can be ternary and binary at the same time.
[106] We thus claim that many of the musical repertoires that are known today for their sense of swing are best understood as using fast non-isochronous pulses at the metric subdivision level, and many of these repertoires stem from Africa or are influenced by African diasporas. However, non-isochronous subdivision does characterize musical styles in Europe (and probably elswhere) too, as shown in the examples of French Baroque performance practice (notes inégales), Viennese waltz (Bengtsson, Tove, and Thorsén 1972; Bengtsson 1974; Bengtsson and Gabrielsson 1983) or Scandinavian folk dance music (Kvifte 2004; 2007; Johansson 2009). Note that here, again, the styles in question are often associated with dancing.
7.3 Non-isochronous rhythms, non-isochronous meters, and metrical theory
[107] Our observations of the timing details in Ngòn and Bire, as well as in the other musics noted above, lead us to conclude that their accompaniment patterns are not simply durational proportions—that is, expressively timed rhythmic groups—but are direct expressions of metrical structure. The kèngèbu (L-S-S) and swing (L-S) accompaniment patterns are examples of context-specific metrical timing patterns, and therefore serve as evidence for London’s “many meters hypothesis,” according to which we acquire timing frameworks not as abstract, merely numerical temporal structures (as traditional metric theory sometimes seems to imply), but as templates that are associated with particular genres, styles, tempo-ranges, performers, and/or pieces (2012, 182–84). When we listen to Ngòn and Bire, and are familiar with Mande music, we entrain to their rhythms, and through that entrainment our temporal expectations and actions will come to match the non-isochronous timings of their accompaniment patterns.
[108] Non-isochrony on the subdivision level is not the only challenge Ngòn and Bire pose for theories of meter and metric well-formedness. In addition to having non-isochronous divisions of the beat, which result in prototypical patterns of long and short beat subdivisions (L-S-S and L-S), Mande drumming practice may also involve further division of the Longs—but not the Shorts. Thus, in addition to its relative length, another distinguishing quality of the Long is its divisibility. This divisibility is related to their absolute values: while the short elements are often too short to permit any additional metric division (i.e., < 200 ms duration), the long elements are usually just long enough to admit metrically meaningful division.
Figure 7.1a. Metric hierarchy with two-beat subdivision levels (binary L-S and ternary s-S1-S2)
(click to enlarge)
Figure 7.1b. Metric hierarchy with two-beat subdivision levels (ternary L-S-S and quaternary s-s-S-S)
(click to enlarge)
[109] The implications for metric well-formedness here are two. First, with the division of the Long but not the Short, an incomplete bifurcation of the metrical hierarchy occurs. Second, the division of the Long maintains the essential non-isochrony in the resulting second level of subdivision (see Figures 7.1a and 7.1b).
[110] Given that the initial conditions for this elaborative subdivision are beats with an uneven ratio, either a binary L-S or a ternary L-S-S, the resultant pattern is also uneven. In Bire, the binary L-S becomes a ternary figure: s-S1-S2, whose “S2” = the “S” of the binary L-S pattern, and whose “S1” and “S2” elements are themselves differentiated by expressive timing patterns. In Ngòn the ternary L-S-S becomes a quarternary figure: s-s-S-S, whose two “s” elements result from the Long element of L-S-S being evenly divided.
[111] In either case, the interpolation must maintain the non-isochrony of the “parent” metrical framework, and so one must avoid interpolating a ratio that might lead to an isochronous figure. For instance, a bifurcation of the Long of L-S into a 1:2 s S (L-S → s-S-S) would transform a 60:40 pattern into a 20:40:40 pattern, raising the possibility of a latent layer of isochrony, especially at slower tempos—which is avoided in Mande drumming. Thus interpolation in Ngòn or Bire is unlike interpolation of a missing articulation in an isochronous meter (e.g., when a 2:1 figure is perceived to be based on a 1:1:1 subdivision), as the result is not an isochronous rhythmic surface.
[112] Furthermore, while one might properly characterize a 2:1 rhythm as an isochronous triplet with a missing or unarticulated element, one would not call the Bire swing or Ngòn kèngèbu patterns (L-S or L-S-S) as “missing” a metrical element. Rather, they are quantitatively multivalent: they can be binary and ternary at the same time, or ternary and quaternary, respectively—but qualitatively stable. Adding a second subdivision level to a swung first subdivision (for instance, adding a ternary s-S-S level to a basically binary L-S rhythm) does change the meter, of course; it increases the density of the lowest level of meter and the depth of the metric hierarchy. But it does not disrupt the metric regularity or ambiguate the metric type—just as adding a sixteenth-note level to an eighth-note rhythm in the context of an isochronous meter does change, but does not necessarily disturb or ambiguate that meter. Moreover, the bifurcated figures in Mande drumming do not lead to a shift of the sense of downbeat, even though the very short “s” is shorter than “S” elements. On the contrary, the anacrustic sense of the S-S elements in Ngòn or of the S2 element in Bire is unaffected by the bifurcation.
[113] In terms of metric well-formedness, the above illustrations involve adjacent pulses at one metric level recurring again at a neighboring level. To put it in terms of London’s metric well-formedness constraints (WFCs), the division of the long element as per Figures 7.1a and 7.1b above creates a bifurcation of the subdivision level of the metrical hierarchy, and, as the lowest/fastest level of metrical structure present, it is also a disruption of what London calls the N-cycle, the fastest periodicity present (whether isochronous or non-isochronous) that establishes the baseline cardinality of the meter. Higher-level periodicities form what London calls “subcycles,” as they are subordinate to the N-cycle and subject to various constraints as to how events on the N cycle can be concatenated. That is, while London’s revision of his WFCs for the second edition of Hearing in Time (2012) permit non-isochronous subdivisions––provided (a) they are not drastically uneven, and (b) that they are yoked to an isochronous beat (see discussion of WFCs 4.1.1 and 4.1.2, in London 2012, 128–29 and passim)––they do not address meters that have alternate pathways on any of its metrical levels. The interpolation of elements of subdivision between some, but not all, onsets of a higher level of metrical structure gives rise to a series of cyclical discontinuities, violations of London’s WFCs 3.2: “All [sub] cycles must be continuous,” and 3.4: “Each subcycle must connect nonadjacent time points on the next lowest cycle” (London 2012, 92). Thus from one point of view, the bifurcations of the long element in Ngòn and Bire are hierarchic orphans; Figure 7.2a gives an illustration of this in the context of Bire. This point of view, however, presumes a kind of continuity based on nested levels of isochrony, and does not consider the range of metrical cycles that may arise in the context of a fundamentally non-isochronous N cycle. If we do so, and take note of how the absolute timing limits on metric elements (i.e., no IOIs < 100ms) may affect long and short elements of a pattern differently, we then can see bifurcation not as discontinuity, but as alternate forms of N-cycle continuity (see Figure 7.2b; one can imagine a similar diagram for alternate continuities in Ngòn).
Figure 7.2a. Bifurcation of the long element in Bire as cyclical discontinuity (click to enlarge) | Figure 7.2b. Bifurcated and non-bifurcated pathways through the long element in Bire as alternate forms of N-cycle continuity (click to enlarge) |
[114] Thus, pieces that involve bifurcated hierarchies like Ngòn and Bire, as well as swung rhythms in jazz, respect the spirit if not the letter of WFCs 3.2 and 3.4. Continuity of the N cycle is maintained, as there are multiple continuities on that level. Likewise, the strict ordering/rotation of the non-equivalent elements in the non-isochronous subdivision cycle prevents clumping (e.g., in Bire, the pattern is always L-S, L-S, L-S, L-S, rather than L-S, L-S, S-L, L-S) and maintains a clear relationship to the isochronous, higher-level beat cycle (i.e., L elements always articulate beat locations). The avoidance of clumping seems to be a strong preference in the creation of non-isochronous meters (Toussaint 2013, 89–90). This insures both the hierarchic integrity of the meter, as either the binary/ternary versions of Bire and ternary/quarternary versions of Ngòn consist of IOIs that are of the same magnitude, as well as the maximal evenness of the meter as a whole.
[115] This suggests there is a dialectic relationship between unevenness and interpolation in bifurcated meters, a relationship that guarantees metric stability despite their ambiguous cardinality: the greater the unevenness (i.e., as the subdivision ratio approaches a 2:1 or 2:1:1 relationship), the greater the likelihood of interpolation (subdivision of the longest element), whether actual in the music or virtual in the mind of the listener. Likewise, to maintain the categorical distinction between the two subdivision classes, the ratio must stay clear of a 1:1 ratio. Thus there is a restricted range in which uneven or “swung” beat subdivisions are possible, as is borne out by the remarkable recurrence of these subdivision ratios in our data as well as that in the studies cited above.
[116] In sum, the non-integer ratios of Bire and Ngòn are not only an optimal timing strategy for avoiding a sense of isochrony on the subdivision level, but also afford specific locations for further elaboration, which allows the player to manipulate rhythmic density and control the level of energy (or “heat”) so crucial to groove-based (dance-, march-, or work-oriented) music, and at the same time maintain the core beat subdivision and its sense of swing.
7.4 The range of possibilities for non-isochronous meters
[117] The non-isochronous metric subdivisions of Ngòn and Bire challenge and enhance our understanding of metric well-formedness: one may have non-isochronous subdivisions yoked to an isochronous beat, just as one may have non-isochronous beats yoked to an isochronous layer of subdivisions. Are there other possibilities for non-isochronous meters? If we consider meters as a coordination of a layer of subdivision, a beat layer, and a higher-level beat cycle (i.e. the measure periodicity), then there are eight logically possible permutations of isochronous and non-isochronous metrical layers, seven of which feature non-isochrony:(26)
Table 7.1. All possible permutations of isochronous and non-isochronous metrical layers
(click to enlarge)
[118] While some theorists and composers describe certain rhythmic surfaces as having constantly changing or “modulating” meters, we are reluctant to call these surfaces metric at all. Even if the beat level is constant, the result is a very limited sense of meter, when the beats do not settle into a stable cycle of entrainment. Nor are we aware of any examples outside of twentieth- and twenty-first century Euro-American art music that purport to have non-isochronous measures. From a comparative perspective, we thus accord limited relevance to possibilities 4, 5, 6, and 8 given in Table 7.1. This leaves only one commonly performed possibility for a meter with two levels of non-isochrony: meters involving both non-isochronous beats and non-isochronous beat subdivisions. This does occur, for instance, in the Norwegian Springar and Polska genres. To account for meter in these pieces, Kvifte (2007, 75) proposed a “common slow pulse” as a reference period that provides a framework for the non-isochronous levels below it. Kvifte also notes the importance of knowing the kinematics of the dances which this music accompanies, as the non-isochronous beats and subdivisions have their analogs in the bodily movements of the dance(r)s.
[119] In their 2010 exchange in MTO, Polak contested the a priori assumption of isochrony on the metric subdivision level in much work of music psychology, music theory, and ethnomusicology, including London’s (2004) original set of metric well-formedness constraints. London acknowledged that the challenges raised by Polak’s careful and detailed analysis of jembe drum ensemble music from Mali required a revision of his WFCs, and noted that “different levels of rhythmic and metrical structure play by different rules. One-size-fits-all WFCs or MWFRs just don’t work; metrical structure is messier, more complex, and more interesting than such simplifying theories will allow . . . isochrony is not required on any level of the metrical hierarchy” (London 2010, [15]). Our collaborative work has reinforced this view and given it more nuance. Not only do WFCs need to be tailored to specific levels of the metrical hierarchy, they also need to be tailored to the particular kind of meter in play—wholly isochronous, non-isochronous beats, non-isochronous subdivisions, or non-isochronous beats and subdivisions. This in turn shows us the necessity of surveying the worlds’ musics most broadly in order for us to have a true understanding of the nature of musical meter in general, as well as the way meter works in any particular style, genre, or culture.(27)
| Correction, August 1 2014: An earlier version of this article had an error in paragraph 92. The following sentence has been deleted: "This latter ratio is close to the 57:43 ratio found by Repp, London, and Keller (2011) in their study of the perception and production of two element non-isochronous rhythms." The ratio reported in Repp, London, and Keller 2011 is 1:.57, not 57:43. |
Rainer Polak
Cologne University of Music and Dance
Institute for World Music and Transcultural Music Studies
50668 Köln, Germany
polak@mail.de
Justin London
Carleton College
Department of Music
Northfield, MN 55057, USA
jlondon@carleton.edu
Works Cited
Arlin, Mary. 2000. “Metric Mutation and Modulation: The Nineteenth-Century Speculations of F.-J. Fétis.” The Journal of Music Theory 44, no. 2: 261–322.
Arnoldi, Mary Jo. 1995. Playing with Time. Art and Performance in Central Mali. Bloomington and Indianapolis: Indiana University Press.
Arom, Simha. 2004. African Polyphony and Polyrhythm. Musical Structure and Methodology. 2nd ed. Cambridge, New York, Paris: Cambridge University Press.
Babbitt, Milton. (1962) 1972. “Twelve Tone Rhythmic Structure and the Electronic Medium.” In Perspectives on Contemporary Music Theory, ed. B. Boretz and E.T. Cone, 148–79. New York: W.W. Norton.
Benadon, Fernando. 2006. “Slicing the Beat: Jazz Eighth-Notes as Expressive Microrhythm.” Ethnomusicology 50, no. 1: 73–98.
Bengtsson, Ingmar. 1974 “Empirische Rhythmusforschung in Uppsala.” In Hamburger Jahrbuch für Musikwissenschaft, ed. C. Floros, H.J. Marx and P. Petersen, 195–220. Hamburg: Karl Dieter Wagner.
Bengtsson, Ingmar, P.-A. Tove, and S.-M. Thorsén. 1972. “Sound Analysis Equipment and Rhythm Research Ideas at the Institute of Musicology in Uppsala.” In Bericht über die 3. Internationale Arbeitstagung der Study Group on Folk Musical Instruments des International Folk Music Council in Stockholm 1969, ed. Erich Stockmann, 53–76. Stockholm: Musikhistoriska Museet.
Bengtsson, Ingmar, and Alf Gabrielsson. 1983. “Analysis and Synthesis of Musical Rhythm.” In Studies of Music Performance. Papers Given at a Seminar Organized by the Music Acoustics Committee of the Royal Swedish Academy of Music, ed. Johan Sundberg, 27–59. Stockholm: Royal Swedish Academy of Music.
Brǎiloiu, Constantin. 1984. “Aksak Rhythm.” In Problems of Ethnomusicology, trans. C. Brǎiloiu and A.L. Lloyd, 133–67. Cambridge: Cambridge University Press.
Charry, Eric S. 2000. Mande Music. Traditional and Modern Music of the Maninka and Mandinka of Western Africa. Chicago and London: University of Chicago Press.
Chernoff, John M. 1979. African Rhythm and African Sensibility: Aesthetics and Social Action in African Musical Idioms. Chicago: University of Chicago Press.
Clarke, Eric F. 1987. “Categorical Rhythm Perception: An Ecological Perspective.” In Action and Perception in Rhythm and Music, ed. Alf Gabrielsson, 19–34. Stockholm: Royal Swedish Academy of Music.
—————. 2000. “Categorical Rhythm Perception and Event Perception.” In 6th International Conference on Music Perception and Cognition (ICMPC) and 4th Triennial Conference of the European Society for the Cognitive Sciences of Music (ESCOM), ed. Chris Woods, Geoff Luck, Renaud Brochard, Fred Seddon, and John Sloboda.
Clayton, Martin. 2000. Time in Indian Music. Rhythm, Metre, and Form in North Indian Rag Performance. Oxford: Oxford University Press.
Collier, Geoffrey L., and James L. Collier. 2002. “A Study of Timing in Two Louis Armstrong Solos.” Music Perception 19, no. 3: 463–83.
Cooper, Grosvenor, and Leonard B. Meyer. 1960. The Rhythmic Structure of Music. Chicago: University of Chicago Press.
Ellis, Mark C. 1991. “An Analysis of ‘Swing’ Subdivision and Asynchronization in Three Jazz Saxophonists.” Perception and Motor Skills 75: 707–13.
Fraisse, Paul. 1963. The Psychology of Time. New York: Harper and Row.
Friberg, Anders, and Andreas Sundström. 2002. “Swing Ratios and Ensemble Timing in Jazz Performance: Evidence for a Common Rhythmic Pattern.” Music Perception 19, no. 3: 333–49.
Gerischer, Christiane. 2003. O Suingue Baiano. Mikrorhythmische Phänomene in baianischer Perkussion. Frankfurt am Main: Peter Lang.
—————. 2006. “Suingue Baiano: Rhythmic Feeling and Microrhythmic Phenomena in Brazilian Percussion.” Ethnomusicology 50, no. 1: 99–119.
Gridley, Mark C. 1985. Jazz Styles: History and Analysis. 2nd ed. Englewood Cliffs, NJ: Prentice-Hall.
Hasty, Christopher. 1997. Meter as Rhythm. Oxford: Oxford University Press.
Hauptmann, Moritz. 1888 The Nature of Harmony and Meter, trans. by W.E. Heathcote. New York: Novello, Ewer, and Co. Originally published in 1853 as Die Natur der Harmonik und der Metrik: Zur Theorie der Musik. Leipzig: Breitkopf und Hartel.
Hood, Mantle. 1982. The Ethnomusicologist. 2nd ed. Kent, OH: Kent State University Press.
Jankowsky, Richard C. 2010. Stambeli. Music, Trance, and Alterity in Tunisia. Chicago: University of Chicago Press.
—————. 2013. “Rhythmic Elasticity, Metric Ambiguity, and Ritual Teleology in Tunisian Stambeli.” Analytical Approaches to World Music 3, no. 1.
Johansson, Mats. 2009. Rhythm into Style. Studying Asymmetrical Grooves in Norwegian Folk Music. PhD diss: University of Oslo.
Kolinski, Mieczyslaw. 1973. “A Cross-Cultural Approach to Metro-Rhythmic Patterns.” Ethnomusicology 17, no. 3: 494–506.
Kubik, Gerhard. 1988. “Einige Grundbegriffe und -Konzepte der Afrikanischen Musikforschung.” In Zum Verstehen Afrikanischer Musik, G. Kubik, 52–113. Leipzig: Reclam.
Kvifte, Tellef. 2004. “Description of Grooves and Syntax/Process Dialectics.” Studia Musicologica Norvegica 30: 554–77.
—————. 2007. “Categories and Timing. On the Perception of Meter.” Ethnomusicology 51, no. 1: 64–84.
Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge: MIT Press.
Lester, Joel. 1986. The Rhythms of Tonal Music. Carbondale: Southern Illinois University Press.
Locke, David. 2010. “Yewevu in the Metric Matrix.” Music Theory Online 16, no. 4.
London, Justin. 1995. “Some Examples of Complex Meters and Their Implications for Models of Metric Perception.” Music Perception 13, no. 1: 59–78.
—————. [2004] 2012. Hearing in Time: Psychological Aspects of Musical Meter, 2nd ed. Oxford: Oxford University Press.
—————. 2010. “Commentary.” Music Theory Online 16, no. 4.
—————. 2013. “Rhythm.” Grove Music Online. Oxford Music Online. Oxford University Press.
London, Justin, Tommi Himberg, and Ian Cross. 2009. “Structural and Performance Factors in the Perception of Anacruses.” Music Perception 27, no.2: 103–20.
Lortat-Jacob, Bernard. 1980. Musique et Fêtes au Haut-Atlas. Paris: Mouton Éd.
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings (1787–1791). New York: Oxford University Press.
Momigny, Jérôme-Joseph de. (1821) 1980 (Reprint). La Seule Vrai Théorie de la Musique. Geneva: Minkoff editions.
Naveda, Luiz, Fabien Gouyon, Carlos Guedes, and Marc Leman. 2011. “Microtiming Patterns and Interactions with Musical Properties in Samba Music.” Journal of New Music Research 40, no. 3: 225–38.
Neuhoff, Hans, Rainer Polak, Timo Fischinger, and Justin London. (Forthcoming.) “Metric Timing Patterns and Categorical Rhythm Perception in Percussion Ensemble Music from West Africa. An Empirical Test of the Listeners’ Cognition and Evaluation.”
Otter, Elisabeth den, and M. Kéïta. 2002. Sogo Bò. La Fête des Masques Bamanan. Bamako: Imprim Color.
Pantaleoni, Hewitt. 1972. “Three Principles of Timing in Anlo Drumming.” African Music 5, no. 2: 50–62.
Polak, Rainer. 1998. “Jembe Music in Bamako: Microtiming as Formal Model and Performance Practice.” Iwalewa-Forum 2: 24–46.
—————. 2007. “Performing Audience: On the Social Constitution of Focused Interaction at Celebrations in Mali.” Anthropos 102, no. 1: 3–18.
—————. 2010. “Rhythmic Feel as Meter. Non-Isochronous Beat Subdivision in Jembe Music from Mali.” Music Theory Online 16, no. 4.
—————. 2012. “Urban Drumming: Traditional Celebration Music in a West African City (Bamako).” In: Hip Hop Africa: New African Music in a Globalizing World, ed. Eric Charry, 261–81. Bloomington: Indiana University Press.
Povel, Dirk-Jan. 1981. “Internal Representation of Simple Temporal Patterns.” Journal of Experimental Psychology: Human Perception and Performance 7, no. 1: 3–18.
Repp, Bruno H. 2005. “Sensorimotor Synchronization: A Review of the Tapping Literature.” Psychonomic Bulletin and Review 12, no. 6: 969–92.
—————. 2006. “Rate Limits of Sensorimotor Synchronization.” Advances in Cognitive Psychology. Special Issue: Music Performance 2, no. 2–3: 163–81.
—————. 2008. “Phase Correction in Sensorimotor Synchronization with Nonisochronous Sequences.” Music Perception 26, no. 2: 171–75.
—————. 2011. “Perception-Production Relationships and Phase Correction in Synchronization with Two Interval Rhythms.” Psychological Research 75: 227–42.
—————. 2012. “Distortions in Reproduction of Two-Interval Rhythms: When the ‘Attractor Ratio’ is not Exactly 1:2.” Music Perception 30, no. 2: 205–23.
—————. 2013. “Systematic Distortions in Musicians’ Reproduction of Cyclic Three-Interval Rhythms.” Music Perception 30, no. 3: 291–305.
—————. 2013. “Sensorimotor Synchronization: A Review of Recent Research (2006–2012).” Psychonomic Bulletin and Review 20, no. 3: 403–52.
Rice, Timothy. 2013. Ethnomusicology: A Very Short Introduction. New York: Oxford University Press.
Riemann, Hugo. 1903. System der Musikalischen Rhythmik und Metrik. Leipzig: Breitkopf und Härtel.
Stone, Ruth. 1985. “In Search of Time in African Music.” Music Theory Spectrum 7: 139–48.
Stover, Christopher. D. 2009. “A Theory of Flexible Rhythmic Spaces for Diasporic African Music.” PhD diss., University of Washington.
Temperley, David. 2000. “Meter and Grouping in African Music: A View from Music Theory.” Ethnomusicology 44, no. 1: 65–96.
Tenzer, Michael, ed. 2006. Analytical Studies in World Music. Oxford and New York: Oxford University Press.
Toussaint, Godfried T. 2013. The Geometry of Musical Rhythm. What Makes a “Good” Rhythm Good? Boca Raton, FL: CRC Press, Taylor and Francis Group.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. New Haven: Yale University Press.
Sound Recordings
Sound Recordings
Camara, Mamadou, N’dia Kanoute, Mamady Dembele, and Mohamed Diallo. 1997 (CD). Khassonka Dunun. Musique traditionelle du Mali. Playasound 65187.
Lortat-Jacob, Bernard; Hassan Jouad, eds. 1979 (LP): Berbères du Maroc. Ahwach. Collection Musée de L’homme (CNRS): Chant du monde LDX 74705.
Olsen, Miriam, ed. 1994 (CD). Maroc. Musique berbère du Haut-Atlas et de l’Anti-Atlas. Collection CNRS/Musée de L’homme: Chant du monde LDX 274991.
Otter, Elisabeth den, ed. 1998 (CD). Dònfòli/Play the music. Bamana and Bozo songs from Kirango, Mali. Royal Tropical Institute: Pan Records KCD 4010.
Footnotes
* The material covered in this article is of interest to music theorists, ethnomusicologists, and researchers in perception, cognition, and motor behavior. While we have striven to make it as accessible as possible for all readers, for those with little or no background in rhythmic theory, the first section of London 2013 can serve as an introduction to issues engaged in this article; for those with little background in ethnomusicology, we recommend Rice 2013; and for those with little background in music psychology/empirical musicology, David Huron’s web resources (e.g., http://musiccog.ohio-state.edu/Music829C/music829C.html) may be helpful.
Return to text
1. The video samples presented in this article were made, unless specified otherwise, by Rainer Polak in Mali in 2012.
Return to text
2. “Beat class” has been used as an analog to pitch classes within the octave at least since Babbitt 1972, where a beat class is defined in terms of a position within the measure (thus, for example, a measure of 12/8 would have 12 distinct beat class locations). Here “beat-interval class” is meant as an analog to pitch-class intervals, as a way of determining the number of “step sizes” one may have within a measure (one for isochronous meters; two or more for non-isochronous meters) and within a beat.
Return to text
3. A flam is a sound created by two successive drum strokes that occur so closely to each other that they merge in the listener’s perception, and are conceived of as a single rhythmic event, analogous to grace notes played by melodic instruments. Flams are well known as an element of rudiments in jazz drumming; however, they are prominent in the playing styles of many other musical traditions and instruments as well.
Return to text
4. We largely take as reference the actual beat duration that the measured element is part of. An alternative option is to take as referent the normalized beat duration of the respective four-beat metric cycle; this was done for rhythm figures longer than one beat in length. For the ostinato accompaniment parts, the two approaches—beat- vs. measure-based normalization—did not make a meaningful difference (<0.1%).
Return to text
5. Drummers in the musical traditions under study are always male; we thus do not use gender inclusive language in this respect.
Return to text
6. In Mande drum ensembles, there are always options for enlarging the ensemble by adding further accompaniment parts. Bamana ensembles can thus integrate more than two bòn drums. In rural Khasonka drumming the basic ensemble of two dundunbas is typically complemented by a huge goblet shaped drum standing on feet, called tantango, which is played by two musicians. In urban settings, the tantango recently tends to be replaced by one or two jembe drums.
Return to text
7. For a more extensive style and performance practice, such as urban jembe playing in the million-strong city of Bamako in the 1990s, this means that there were over 60 clearly distinct individual dundun hook themes in common knowledge and practice, which characterized the more than 60 pieces of the standard repertoire (Polak 2012).
Return to text
8. In West African percussion music, phrases can take up rhythmic drive and develop forward propulsion over stretches of time that are longer than typical anacruses, but which share with the anacrusis the feature of aiming ahead towards a point of rhythmic gravity and conclusion rather than starting from such a point (cf. Chernoff 1979, 56; Locke 2010, 96).
Return to text
9. Here and below, standard deviations are given as a measure of the variability of a durational unit. Statistics within the main body of the text have been kept to a minimum; results of comparisons of means (T-tests and ANOVAs) and measures of statistical significance are given in the footnotes. Two other caveats: first, when results are described as “significant” this is meant in the technical sense of statistical significance (i.e., p < .05); and second, given the large sample sizes most results are (unsurprisingly) statistically significant, though effect sizes are generally quite small.
Return to text
10. One-way ANOVA result: F (3,2312) = 37.67, p < .001.
Return to text
11. Multivariate ANOVA F (1.99, 4598.99) = 19,082.47, p < .001; interaction between beat and performance F (9.96, 4598.99) = 77.66, p < .001; Greenhouse-Geisser correction applied in all cases).
Return to text
12. One way ANOVA for each syllable (ensemble as dependent variable): Bu, F (2, 2313) = 227.27, p < .001; Kèn, F (2, 2313) = 15.12, p < .001; Gè F (2, 2313) = 152.80, p < .001).
Return to text
13. Post-hoc syllable-by-syllable comparisons (Bonferroni and Games-Howell) for each ensemble were all highly significant (p < .001), save for Kèn and Gè as performed by Ensemble 3, which was non-significant.
Return to text
14. One-way ANOVA showed significant differences for all three syllables: Bu F (2, 1197) = 12.57, p < .001; Kèn F (2, 1197) = 6.95, p = .001; Gè F (2, 1197) = 33.52, p < .001. For Gè, Bonferroni and Games-Howell post hoc contrasts were highly significant, p < .001.
Return to text
15. Kèn F (15, 2292) = 21.07, p < .001; Gè F (15, 2292) = 14.99, p < p < .001; Bu F (15, 2292) = 11.59.
Return to text
16. All T-tests reported are two-tailed.
Return to text
17. ANOVAs for both Beat X Performance and Performance X Beat were all highly significant (p < .001); the only post hoc contrast (both Bonferroni and Games-Howell) that was not significant was the contrast between Beats 2 and 3 in the Performance 2.4.
Return to text
18. A one-way ANOVA showed a main effect of performance (F (3, 1880) = 94.23, p < .001).
Return to text
19. One-way ANOVA for Syllable X Performance found Bu: F (5, 260) = 7.41, p < .001; Kèn: F (5, 260) = 6.52, p < .001; Gè: F (5, 260) = 21.66, p < .001.
Return to text
20. One-way ANOVA for Beat X Performance found: Beat 1.1: F (2, 321) = 48.15, p < .001; Beat 2.3: F (2, 321) = 9.88, p < .001; Beat 3.3: F (2, 321) = 2.00, p = .138; Beat 4.3: F (2, 321) = 45.23, p < .001). Post-hoc contrasts (Bonferroni and Games-Howell) showed that the differences between Performances 2.1 and 2.2 are non-significant for Beats 1.1 and 2.3.
Return to text
21. One-way ANOVAs for both Performance X Motive and Motive X Performance were all highly significant, as were post-hoc tests for differences between motivic elements within each performance.
Return to text
22. In Recordings 1.1–1.3, 25–38% of all beats show the denser subdivision. Recordings 1.4 and 1.5 do not feature the lead part. The youth ensemble’s (Recording 1.6) lead player does not perform any subdivision more elaborate than the kèngèbu pattern itself.
Return to text
23. A one-way ANOVA for Subdivision Element X Performance was highly significant (p < .001) for all cases (lead bell, lead drum, and accompaniment bell). Even with the variability in the data, post hoc tests (Bonferroni and Games-Howell) showed that ratios for P2.3 and P2.4 were essentially alike for all three elements (i.e., all differences were non-significant). Similarly the Accompaniment Bell was alike in P2.1 and P2.2. The other parts in Performances 2.1 and 2.2 show a more irregular pattern of correlation (Lead Bell in P2.1 is like the Lead Bell in P2.4 but not P2.2 or P2.3; Lead Drum in P2.1 is like the Lead Drum in P2.2 and P2.3 but not P2.4), a reflection of the greater overall variability in P2.1 and P2.2.
Return to text
24. As noted as WFC 4.12 in London 2012, “if the IOIs on the N-cycle are non-isochronous, their absolute lengths must be such as to avoid ambiguities and contradictions; (S) must be > 1/2 (L)” (London 2012, 128).
Return to text
25. Given the 100 ms limit (or thereabouts) on absolute duration/IOI of the shortest element of metrical subdivision, an additional constraint, at least potentially, is that the 25:35:40 ratio, rather than the 20:40:40, gives the players a bit more “tempo room” as the performance accelerates.
Return to text
26. We thank Peter Keller for this observation.
Return to text
27. This research has been supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG: PO 627/6-1). Parts of it were presented at the Musical Metre in Comparative Perspective conference (Cologne University of Music and Dance, April 4–6, 2013) and the International Symposium on Performance Science (University of Music and Performing Arts Vienna, August 28–31, 2013), where the authors gained valuable insights from discussions of their work.
Return to text
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editoral assistant
Number of visits:
33898