Meter Metrics: Characterizing Relationships Among (Mixed) Metrical Structures
Mark Gotham
KEYWORDS: meter, formalization, similarity, twentieth-century music, Aksak
ABSTRACT: “Consideration of a metric context is indispensable for a complete understanding of rhythm” (Toussaint 2013, 16). In order to discuss the nature of a rhythm or its compositional development, it is necessary to account for the metrical context(s) in which it appears. In music that moves among a variety of metrical structures, it is also necessary to account for the relationships that exist between those meters. This article provides a detailed characterization of those relationships. What is more, the relationships introduced here may be discussed independently of any rhythmic parallel, illuminating purely metrical aspects of temporal organization, and thus offering an altogether new analytical perspective on repertoires in which metric change is an important compositional parameter.
This study identifies a variety of metrical relationships, defines them (mathematically where appropriate), and assesses them for perceptual and musical significance, including the rarity of their occurrence. The focus is on “mixed” metrical structures that systematically use more than one type of duration on the same level, such as both “short” and “long” beats (which may or may not correspond to 2- and 3-unit groupings).(1) “Simple” meters (with only one type of beat) are also discussed for the sake of completeness and because all are used together in the relevant repertoires (which include much twentieth-century Western music, some popular musics, and “world” musics including the Balkan Aksak style). The breadth of this potential application is a principal asset of the theoretical apparatus presented.
Copyright © 2015 Society for Music Theory
1. Introduction
[1.1] Rhythm and meter are ubiquitous, finding expression in phenomena as fundamental to the human experience as the beating heart and bipedal walking, yet theoretical engagement with those parameters has traditionally been a secondary concern of music theory, presumably because pitch is a more important compositional parameter in the primary target repertoire: common-practice, Western tonal music. A late twentieth-century resurgence of interest in temporal matters engaged the relationship between rhythm and meter, as well as the definition of meter as an interaction between structural levels,(2) and a great variety of diverse work has been carried out since. Still, much remains to be done.
[1.2] Mixed meters particularly invite new theoretical work. They offer rich compositional possibilities and are a core component of many diverse repertoires (outside common-practice, Western tonal music), yet no comprehensive survey of those possibilities has yet been undertaken beyond merely listing the different meters themselves.(3) This article undertakes such a theoretical survey, charting the relations that can exist among mixed (and simple) meters, and frequently mapping these meters and relations on mathematical spaces that can be considered analogous to well-known characterizations of tonal pitch space.
[1.3] There is some precedent for mathematical metrical spaces analogous to tonal pitch space; and as with models of tonal pitch space, models of metrical spaces have traced a pattern of increasing complexity and sophistication.(4) Tonal space was first represented on the one-dimensional circle of fifths,(5) before the introduction of the two-dimensional Tonnetz, the three-dimensional cylinder, and spaces with more than three dimensions.(6) In the case of meter, Cohn (2001) develops a two-dimensional space for charting simple metrical structures (a space not to be confused with the two-dimensional “ski hills” on which those meters are defined), and Murphy’s (2009) “metric cubes” extend the same ideas to a third dimension, finessing some issues associated with Cohn’s model in the process. However, both Cohn and Murphy develop only a limited set of metrical relationships, due to their focus on metrical dissonance in tonal music, especially Brahms.(7) (The same is true of Leong’s [2007] related work on Humperdinck and Wagner.) They therefore do not engage with mixed meters or the wider set of relations that exist between those structures.
[1.4] This article is dedicated primarily to that wider set of meters and metrical relations, providing a basis for analyzing any repertoire in which change between mixed metrical structures is significant. The study begins with preliminary matters of defining and representing meter. The relationships are then introduced and informally assessed for the rarity of their occurrence—an issue that has rightly concerned the analytical community since at least Dunsby’s “Criteria of Correctness in Music Theory and Analysis” (1994). Musical examples serve both to illustrate the relations and to present them for analytical scrutiny; footnotes supply mathematical formalizations of the relations, further analytical commentaries, and lists of repertoire examples; and numerous tabular and graphical summaries illustrate the structure of relations and their interaction. The concluding section includes the most comprehensive summary of family entailments among the relations (Figure 24), as well as a glossary of the relations and properties, and a model of three-dimensional space that accommodates as many as possible of the meters and relations (Figure 25). This space is a useful representation, but the focus of the study is on characterizing each metrical relation in its own terms. To that effect, each is discussed separately and presented in its own mathematical space (where appropriate). These spaces provide the clearest visual aids for conceptualizing the various relations.(8)
2. Defining, Describing, and Representing Meter
[2.1] This is a theoretical study describing a priori relations between metrical structures. The complexities of whether and how these relationships might be parsed by a listener based on cues in the composition or performance are considered only secondarily in the context of certain relations, and through application in the course of brief analyses. Some supplementary comments concern apparent psychological preferences for metrical forms and—relatedly—the extent of usage in musical practice.
[2.2] For the present purposes, “meter” is operationally defined as an hierarchical framework for temporal events. Only very basic criteria for metrical well-formedness are required here. Indeed, only one criterion is consistently essential: that the majority of temporal events belong to a categorical metrical position such as “on the downbeat.” Although exceptional ametrical events are admissible (grace notes, trills, etc.), a multi-leveled metrical system in which (most) events have a specific metrical identity is required for almost any of the relations advanced here to have meaning.(9) Put another way, this study deals with “structural” rather than “micro-” timing.
[2.3] The other initial criteria imposed are the presence of a common fast pulse (CFP) and the grouping of that pulse level and all higher levels into twos and/or threes (both coexist within the same level in the case of mixed meters).(10) In many cases, these criteria may both be relaxed to include any other system of two beat-types (such as a “Long” versus “Short” pairing) that is excluded by the CFP.(11) This flexibility is potentially important, especially at fast tempos in which the CFP falls outside the limits of metrically useful pulses.(12) Many of the relations discussed here could also be extended to a system of three beat types (short–medium–long), though the grounds for doing so are questionable at best.(13)
[2.4] In discussing different kinds of metrical relations, it will be necessary to refer to different aspects of a meter’s structural identity. Therefore, although it is tempting (and eminently possible) to insist on a single, consistent naming system for all meters in all contexts, it is much truer to the subject-matter to use a small range of nomenclatures, referring to the relevant structural properties of each meter directly. Meter has, of course, been represented in a number of different ways.(14) Four main representations will be used in this study.
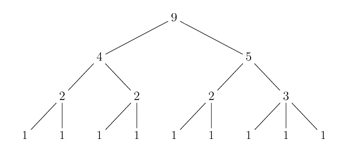
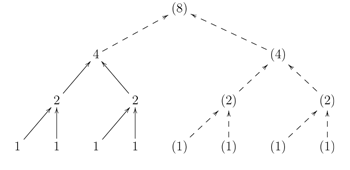
Figure 1. A ‘tree’ structure representation of meter ((22)(23))
(click to enlarge)
[2.5] Meters will frequently be described by an ordered succession of duple and triple beat groupings (twos and threes).(15) 22223 therefore refers to a 5-beat, 11-pulse meter. Nested brackets may be used to differentiate between different higher-level groupings of the same beat succession, such as ((2,2)(2,2,3)) and ((2,2,2)(2,3)). “Tree” structures are also used to convey this ordered, hierarchical information.(16) Trees are a favored method for representing meters as well as many other hierarchical structures, lending a mathematical formality as well as an intuitive graphical representation which is perhaps most familiar from diagrams of the “family tree.” Figure 1 demonstrates this representation for the meter ((2,2),(2,3)). Here, the lowest level comprises nine equal, CFP units (1s), which are grouped as shown into four beats: three duple and one triple. At the next structural level, these four beats are grouped into two parts (unequal halves) of four and five units’ length, and finally into one part encompassing the whole structure.
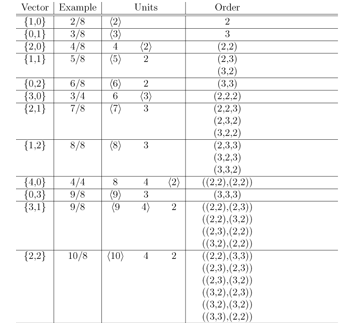
[2.6] Two further notations are used for cases where it is useful to represent the content of a meter without reference to the order of beats. First, this article introduces the “meter vector,” which presents two numbers in curly brackets to designate the number of duple and triple beats respectively. For instance, (22223) would be represented as {4,1} as it has four duple beats, and one triple. Additionally, meters are also described according to the number of units in each metrical level, in this case ⟨11 5 2 1⟩.
[2.7] This “units-per-level” representation may also be made more efficient by establishing grounds for redundant information. According to the well-formedness criteria of grouping by twos and threes, a five-unit level necessarily reduces to two units at the higher level. As such, the example of ⟨11 5 2 1⟩ in the preceding paragraph may be reduced to ⟨11 5⟩ without loss of structural information. Further reduction can be effected by assuming binary grouping and division between levels except where specified,(17) and a preference for compound meters over mixed meters.(18) In that case, ⟨9⟩ refers to {0,3} while ‘⟨9 4⟩’ would be necessary to describe the meter vector {3,1}. As such, the “units per level” system may be used as a shorthand for however many consecutive levels are necessary to convey all of the non-simple-binary organization of a meter. That said, in many cases it will be desirable (for both musical and formal reasons) to retain an account of which metrical levels are actually expressed in a musical passage.(19)
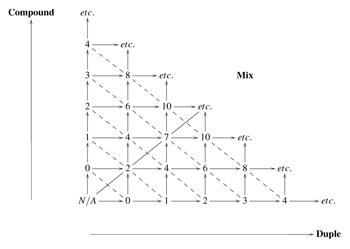
Figure 2. A recursive chart for metrical structures
(click to enlarge and see the rest)
[2.8] These representations are designed to conform (insofar as possible) to existing formalisms in the music-theoretic literature.(20) However, the focus on mixed meters requires extensions and modifications. For instance, the “meter vector” introduced here is clearly not necessary for representing simple meters, while the representations of proportional schemas between levels which are important in studies of simple meters are only passingly relevant here.(21)
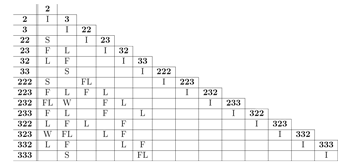
[2.9] Figure 2 provides a list of all well-formed metrical structures from two to twelve pulse-units in length.(22) The chart is recursive and so may be continued indefinitely to longer meters as necessary. Each of the modes of representation described is included in the chart (excepting tree structures for obvious reasons), along with examples of time signatures which may be used to represent the whole metrical structure described. In the units-per-level column (“units” on the chart), the unit numbers for each level are given, and the essential, reduced representation is delimited by angle brackets.
3. Types of Relations I: Grouping Commonalities
Figure 3. Corresponding extracts from the opening and recapitulation of the third movement of Martinů’s Les Fresques de Piero della Francesca, showing the same musical material notated in different ways
(click to enlarge)
[3.1] We may now begin to chart the various relations between meters, beginning with a class of relationships concerning the grouping of metrical units between levels
[3.2] Here, both meters have one level of ternary organization ⟨3⟩ at the same level—the primary level for marking tactus beats; however, “equivalence” also holds when the corresponding groupings take place at different metrical levels. For instance, all meters with exactly one level of ternary grouping may be represented by the metrical structure ⟨3⟩ (assuming binary grouping on all other levels). If 3/8 follows 3/4 with the eighth-note pulse level held constant, then the two meters are still equivalent, but the ternary grouping occurs on a different metrical level and is therefore a considerably different entity to the counting musician. Let us then define the relation identity (I) for equivalent meters where the tempos also correspond.
Figure 4. A reading of ‘The Grudge’ from Tool’s album Lateralus, based on the migration of a single 5 level among binary groupings on other levels
(click to enlarge and listen)
[3.3] Meters which are equivalent but not identical (E- but not I-related) may assume musical significance through a variety of means, which are not limited to the obvious correspondences of augmentation or diminution. For instance, Figure 4 shows how migrations of a single ⟨5⟩ across metrical levels in equivalent meters may be used to parse successive passages in the opening of Tool’s “The Grudge.” At the start (Figure 4a), 5/16 is strongly asserted by the repetition, especially of the treble part.(25) Version 4b follows 4a, continuing with the same riff (shown by the under-stave brackets), though removing the treble part. This small change makes the passage more readily parse-able in terms of a 5/8 with limited syncopation (that is, with regular counting at the eighth-note level). 4c is a bridge-like passage in which the full pattern clearly repeats at the 5/4 level (though this is complicated by internal repetitions), and in 4d the total span and the changes in subdivision correspond to a 5/2 grouping.(26) The commonality may be identified as the use of equivalent ⟨5⟩ meters, while the difference may be shown by including representation of the other levels used (such as ⟨5 2⟩ for 5/16 as compared with ⟨10 5 2⟩ for 5/8 in this case).(27)
[3.4] Finally, it may also be useful to have a notion of partial grouping commonality (G) for cases where meters share some aspects of common grouping, but not their whole structures. This is a much weaker form of the same relation, which is rarely of statistical significance given the few options for grouping structure within the limits of well-formedness. Partial grouping commonality seems most likely to assume significance where meters share the same number of units at the counting levels—a relation more directly accounted for by the cardinality relations described in the following section.(28)
4. Types of Relations II: Cardinality Relations
Sub-Tactus Pulse Cardinality (P)
[4.1] Two forms of cardinality relation are discussed here. The first, sub-tactus pulse cardinality (P), holds between meters which share the same number of pulse units at the sub-tactus level, whatever the nature of their higher-level grouping. For instance, in Dave Brubeck’s iconic Blue Rondo à la Turk, the repeated four-measure riff in the A sections comprises three (2223) groupings followed by one (333). The principal relation between the two meters is that both are nine pulse-units long.(29)
Figure 5. An extract from Copland’s Appalachian Spring (reh. 11 and also 3 bars before reh. 14), in which the motivic correspondence between the two measures emphasizes their similar sub-tactus pulse cardinality
(click to enlarge)
[4.2] Apart from exact cardinality equivalence, even having merely similar cardinalities at the sub-tactus pulse level (differing by only one unit, for instance) can express important musical considerations such as motive truncation or extension. For instance, 4/4 and 7/8 are clearly very different in terms of their metrical grouping structures, however, their similar sub-tactus pulse cardinalities (of eight and seven units respectively) can be musically relevant. Figure 5 reproduces an extract from Copland’s ballet Appalachian Spring.(30) The motivic similarity between the consecutive measures could not be clearer: the pitch profile is preserved intact, while one eighth note’s duration is removed from the
[4.3] The kind of motivic relation demonstrated in the Copland example is common and may operate over longer passages as a more persistently important compositional device; it is featured prominently in the music and theoretical writings of both Messiaen and Bartók, for instance.(31) See, for instance, mm. 45–47 and 52–54 of the first movement of the Music for Strings, Percussion, and Celesta, in which a nine-unit idea is truncated to eight and then seven in consecutive measures, and the fourth movement of the Concerto for Orchestra, in which a motive alternates between four and five units (as shown in Figure 19, below).
Beat Cardinality (B)
[4.4] Beat Cardinality (B) holds between meters with the same number of beats at the tactus (counting) level, whatever differences there may be between the meter vectors, the ordering of beat types, and the higher-level organization.(32) For instance, where that beat is felt at the x/4 rather than the x/8 level, 11/8 ⟨11 5⟩ and 5/4 ⟨5⟩ both have five beats and thus are B-related.
[4.5] This relation is of particular relevance if we take a step away from the confines of traditional Western Classical notation.(33) Transcribing aurally transmitted music frequently results in a simplification of the timing patterns.(34) For instance, the requirement to identify each beat as a duple or triple grouping of a CFP is frequently contrary to the spirit of the original.(35) The presence of a beat or counting level is usually much clearer than the specific proportional relationship between the durations of those beats unless they are explicitly subdivided in comparable ways. Indeed, it has been suggested that Aksak musicians think only at the beat level rather than the pulse level.(36) Equivalent beat cardinality is a way of reflecting that emphasis.
Figure 6. An illustration of the relevance of the B relation in an Hungarian folk song as transcribed by Bartók
(click to enlarge)
Figure 7. A vector space for the B and U relations
(click to enlarge)
[4.6] Consider, for example, the Hungarian folk song in Figure 6 as transcribed by Bartók (1981, no. 307, 302). Bartók uses two time signatures to notate this melody—(233) and (223)—and considers the first beat of each measure to be the only one which is subdivided in a metrical way. Without explicit subdivisions, the distinction between duple and triple beats (short and long) may not be clear, especially with the extent of ametrical embellishments used. In any case, the beat equivalence relation points to an important commonality between the two meters.
[4.7] The beat equivalence relation is one for which the formal system of duple and triple beats may be relaxed to any other categorical pairing, such as L[ong] and S[hort]. This assumes an importance especially where the limits of perception mean that it is not possible to use the CFP.(37) In either case, we can map similarity of beat cardinality on a simple lattice space, as shown in Figure 7.(38) The two dimensions of Figure 7 correspond to the number of duple or short beats (x axis) and triple or long beats (y axis). The meter vector expresses a coordinate for the beat content. Beat cardinality equivalence (B) holds between meters on the dotted-line diagonals, while the solid arrows indicate the addition of one beat. The type of beat added corresponds to the direction (+x for duple beats and +y for triple).
[4.8] If necessary and appropriate, further beat-types could be added to this space to add metrical categories such as a “medium” beat. To achieve this, add the orthogonal z-dimension and express the three beat types in the form {x, y, z}.
Interlude: A Short Example of Pulse and Beat Cardinality Combined
Figure 8. Measures 26–30 of Ralph Vaughan Williams’s Fantasia on a Theme by Thomas Tallis, as an example of pulse (P) and beat (B) equivalences (shown by brackets below the staves), as well as the structural equivalence (E, shown above the staves)
(click to enlarge and listen)
[4.9] Ralph Vaughan Williams’s Fantasia on a Theme by Thomas Tallis provides a neat example of both main cardinality relations—pulse equivalence and beat equivalence—used in the same succession. Vaughan Williams sets the theme predominantly in 3/4, but includes occasional 6/8 measures.(39) Figure 8 shows the tail end of this theme in a reduction of Vaughan Williams’s score. Brackets below the staves identify the cardinality relations as we move from ⟨12 6⟩ to ⟨12 4⟩, with 12 pulse units in common, a “P” (pulse equivalence) relation, and from ⟨12 4⟩ to ⟨8 4⟩, with four beats in common, a “B” (beat equivalence) relation. Brackets above the staves indicate the regular two-measure phrasing (which has been used with remarkable consistency up to this point in the work),(40) and draw attention to the rhythmic diminution in the melodic part and the concomitant “E” relation which holds between the two measures of 3/4 and the first measure of 6/8 that follows (both ⟨12 6 2⟩).
Unordered Subset Relation (U)
[4.10] The beat cardinality relation does not consider the order of beats, and it is also useful in this context to introduce an unordered subset relation (U) for similarity (but not identity) of beat content. One meter is an unordered subset of another if it has fewer instances of one beat class, and fewer or an equal number of the other.(41) For instance, 7/8 in any of its three ordered forms has the meter vector of {2,1} and unordered subsets of 1/4 {1,0}, 2/4 {2,0}, 3/8 {0,1}, and 5/8 {1,1}. Among these, {2,0} and {1,1} are the most closely related: each subset involves the removal of just one beat. These relations correspond to single steps along the vertical or horizontal axes of Figure 7 (diagonals involve at least two beat changes). All other U relations are, by extension, successions of individual beat removals. The solid arrows of Figure 7 indicate the superset relation.
Figure 9. The number of unordered subsets for each meter, showing that meters with the most equal contribution of the two beat types are the most connected in this regard
(click to enlarge)
[4.11] Figure 7 also illuminates the fact that different meters have different numbers of unordered subsets.(42) Excluding the trivial non-meter {0,0}, the corresponding number of unordered subsets for each of the meter vectors in Figure 7 is given in Figure 9. This graph shows that mixed meters nearest the central diagonal (indicated here by solid diagonal lines) have the most unordered subsets compared with other meters of equivalent beat cardinality (indicated by dotted-line diagonals, as in Figure 7). For instance, meter {1,1} has two unordered subsets, but the other two-beat meters {2,0} and {0,2} have only one each. It seems that a more equal use of the two beat types makes for a more connected meter in this regard.
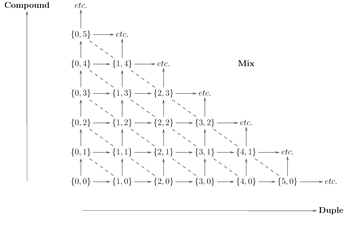
[4.12] The relationship between a meter and the beat types added to it is significant. Where only duple or triple beats are used in a meter, adding another beat of the same type preserves that consistency. Adding a beat of the opposite type makes the simple meter become mixed at that beat level. Movement among the purely duple meters (in the left-most column of Figure 7) or the purely compound meters (in the lowest row) may be taken as the simplest form of beat addition, motion among the mixed meters in the middle to be a secondary type, and a transition between simple and mixed to be the most significant alteration. The following table represents this relationship at the beat level.
| Addition of a duple beat | Addition of a triple beat | |
| Duple meter | Duple meter | Mixed meter |
| Compound meter | Mixed meter | Compound meter |
| Mixed meter | Mixed meter | Mixed meter |
Of course, adding a duple beat to a duple meter may still lead to a mixed structure at higher levels for meters of beat cardinalities greater than four; however, at levels higher than the beat, mixed metrical structures are often much less keenly perceptually salient.(43)
5. Types of Relations III: Order Relations
[5.1] The unordered subset relation is rarely of musical significance on its own terms. Instead, musically significant instances of the U relation tend to be accounted for by more restricted relations in which some aspect of the ordering is also held in common. This section sets out relationships between metrical structures based on commonalities of their orderings.
Saturation (S)
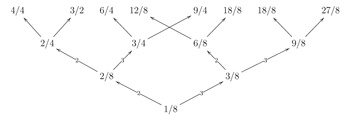
Figure 10. Saturation by multiplication of duple and triple groupings
(click to enlarge)
Figure 11. The Saturation relation in Copland’s Symphony no. 3, movement 3, rehearsal number 72ff
(click to enlarge)
Figure 12. A ‘tree’ structure representing of the Saturation relation between two binary meters (such as 2/4 and 4/4)
(click to enlarge)
[5.2] “Saturation” holds between two meters when the larger can be fully expressed by successive instances of the smaller.(44) For instance, 9/8 may be formed by three successive instances of 3/8. Indeed, if the 3/8 passage has a three-measure hypermetrical structure, then the two are formally equivalent. Figure 10 demonstrates how this relationship holds among simple meters—the longer meter is equivalent to either two or three successive instances of the shorter one.(45)
[5.3] Saturation is one metrical relation and graphic space that has been described in the existing literature on simple meters;(46) however, saturation may hold with any natural number multiplier and is equally applicable to mixed meters. For instance, 10/8 ((2,3),(2,3)) is saturated by two instances of 5/8 (2,3).(47)
[5.4] Figure 11 shows a simple illustration of the saturation relation as used in the third movement of Copland’s Symphony no. 3. The two-beat ostinato shown occurs predominantly in 4/4; however, in the measure before reh. 73, an anomalous 2/4 measure indicates that binary grouping at this level is not consistent. This passage could alternatively have been notated in 2/4 throughout (with varied hypermetrical groupings by implication only) or with one 3/2 measure that subsumes the two measures before reh. 73. In any case, 4/4 is a saturated superset of 2/4, and that relation is made explicit by the musical context shown here.
[5.5] Figure 12 represents this form of the Saturation relation as a tree structure. Solid lines indicate the grouping of the smaller meter (2/4), while dashed lines show the equivalent structure of the larger meter (4/4). This diagram shows how close the saturation relation is, especially between binary meters assuming a binary hypermetrical grouping.
Ordered Subset Relations (O)
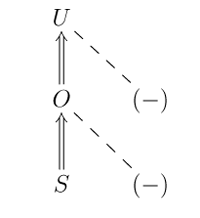
Figure 13. The family structure of entailments for the unordered (U), ordered (O), and saturation (S) relations
(click to enlarge)
Figure 14. Ordered subset relations (including saturation) for meters {1,0} to {0,4}
(click to enlarge)
Figure 15. Further generations of F, L, and W relations
(click to enlarge)
[5.6] Three types of non-saturated order relations may be defined according to the location of the shorter meter within the longer one: “First” (“F”) where it occurs at the start, “Last” (“L”) for the end, and “Within” (“W”) for anywhere else.(48) Any combination of these may hold concurrently, with or without the S relation.(49) The S relation entails at least F and L in the case of binary saturation—between (23) and ((23),(23)) for instance—and requires W also for ternary saturation—between 23 and ((23),(23),(23)). S is a restricted case of O, which in turn is a restricted case of U, as shown in Figure 13.
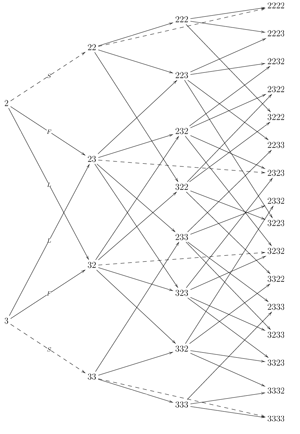
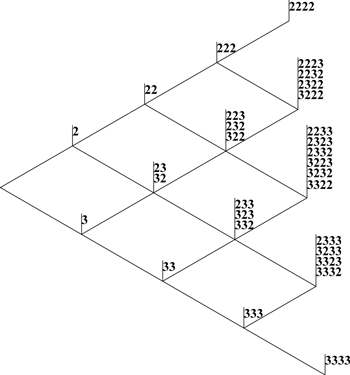
[5.7] Figure 14 sets out ordered subset relations among meters of beat cardinality 1–4. Meters are represented by their ordered forms, and those of the same cardinality appear in the same column. Solid lines indicate the presence of an order relation between two meters of neighboring cardinality. For the sake of clarity, order relations are only shown among meters of neighboring beat cardinality (first generation). Order relations among non-neighboring cardinalities (higher generations) may be found by following successive connected lines (such as from 3 to 32 to 232). “W” cannot hold between meters of neighboring cardinality because the beat cardinalities of W-related meters must differ by at least two.(50) In that sense, W may be thought of as a higher generation relation formed by a combination of F and L relations (for instance connecting 3 with 232 via 32 or 23).
[5.8] W and other higher generations of O relations may be formalized and generalized to some extent. Applying the same relation twice preserves that relation between the original and final result. This is to say that the relations are “transitive,” so if α F β (read “meter α is in the F relation with meter β”) and β F γ then α F γ. For instance, α, β and γ could stand for 3, 32, and 322, which are all in the F relation within each other. Conversely, mixing F and L relations results in W. For instance, 3 L 23 and 23 F 232, so 3 W 232.(51) These results indicate the minimal commonality; other order relations may hold depending on the initial meter and the type of beats added. For instance, 23 L 323 and 323 F ((323)(23)), so 23 W ((323)(23), but also 23 L ((323)(23)).
[5.9] Figure 15 shows all the order relations among meters of beat cardinalities 1–3. What begins to emerge here is the intuitive fact that the combination of low- and high-cardinality meters generates the greatest number of O relations. As was the case for the U relation, O relations are also more common among mixed meters than simple meters. This can been seen in Figure 14, where more lines connect mixed meters (in the middle of the diagram) than simple meters of the same cardinality (at the top and bottom extremes). It seems that mixed meters enjoy a greater number and diversity of connections than their simple counterparts. It is intuitive that a concept of ordering would be of more interest in mixed meters, in which the different lengths of beat make a concept of ordering meaningful, but it is less obvious that these meters would also be more connected in terms of order relations.
[5.10] Ordered subset relations may assume musical significance in a number of different ways. They may approach the close commonality of the saturation relation, where the smaller meter is nested within a structural level of the larger one. For instance, (22) may be considered a more natural ordered subset of (22)(23) than of (223), because it articulates an intermediary level of ((22)(23)) that is not present in (223). Nesting is only possible where the difference between the meters’ lengths is sufficient to define a separate structural level. For the lowest cardinalities, this means the addition of just one beat (for instance, 2–22). For higher cardinalities, two beats is the minimum addition. For instance, this kind of nesting can hold between meters of beat cardinality two and four, or three and five, but not between three and four. This kind of nested order relation is the closest that meters which do not divide into equal parts—such as (22)(23)—can get to a saturated subset relation (connecting with 22 and 23 in this case).
Figure 16. The L relation as manifest in Djoudjeff’s transcription of a Bulgarian folk song, connecting ‘5/16’ (23) and ‘9/16’ (2223) meters (1931, 344)
(click to enlarge)
[5.11] The F and L relations appear to have a particular resonance with compositional practices.(52) For instance, it is relatively commonplace to find a passage in which different mixed meters are used, all of which share some distinctive element like having a single, anomalous triple beat at the end.(53) This becomes an orienting part of the musical structure. The end of the first movement of Dumbarton Oaks provides a ready example. Stravinsky introduces a rising figure in the clarinet at reh. 20, mm. 3 and 5 (9/16, 2223) and this figure recurs increasing frequently in different mixed meters with a single triple beat at the end of the bar.(54) Accordingly, all of these meters share the “Last” ordered subset relation.
[5.12] The relation also appears to be common in Aksak repertoires. Figure 16 shows an example of the same kind of L relation, which Djoudjeff 1931 discusses in conceptually similar terms (including the relation of the musical and textual meter). According to Djoudjeff’s transcription, two meters are used: (23) and (2223). As shown in Figure 17, this L relation is also nested according to the well-formedness criteria used in this study; notice how similar this is to the saturation relation in Figure 12. Only non-nested forms of order relations result in a partial re-grouping at higher levels. Figure 18 shows a case of this re-grouping for the L relation between 5/8 and 7/8.
Figure 17. The nested L relation between the (2,3) and ((2,2),(2,3)) meters in Figure 16 (click to enlarge) | Figure 18. The (non-nested) L relation between (2,3) and (2,2,3) meters (click to enlarge) |
6. Types of Relations IV: Vector-Identical Order Relations (and “Complementation”)
[6.1] The ordered subset relations (including saturation) all concern meters of different beat cardinality (and thus also of different meter vector). We now turn to types of order relations that may hold between meters with the same meter vector: “vector-identical” (V) meters.
Rotation (R)
[6.2] We begin with “rotational equivalence” (R).(55) Imagining the meter as a cycle, different rotations of the same beat succession may be achieved by starting at a different position on that cycle (a “shift of modal starting point,” to use Pressing’s terminology [1983, 40]). Indeed, for aurally transmitted music, it may be obvious that a pattern is repeating, but much more problematic to assert a particular starting point. Rotational equivalence reflects this.
[6.3] Any meter with only a single entry for either duple or triple beats will have rotational equivalence between all of its orderings.(56) In those cases, the rotational equivalence between forms is guaranteed by the vector identity that holds between them. For meter vectors with two or more of both beat types, vector identity does not automatically entail rotational equivalence. In short, rotational equivalence is a restricted case of vector identity.
[6.4] For meters with more than one entry for duple or triple beats, there emerge separate sub-groups of rotationally equivalent permutations. For instance, there are 4!/2!(2!) = 6 permutations of {2,2}. Among these, 2323 is rotationally equivalent only to 3232, while 3322 is equivalent to 2332, 2233, and 3223. These may then be thought of as divided into two meaningful sub-classes of the orderings. The number of rotations for any metrical ordering is given by the number of beats; however, these may not all be distinct solutions. Hence 2323 has only one distinct rotationally equivalent solution, because rotating the meter by two beats results in the original pattern.(57) For simple meters (such as 2222), there is only one distinct ordering.
[6.5] Rhythmic rotation is a commonly used musical device, particularly in West African drumming,(58) as well as other repertoires such as minimalism, as in Reich’s phase-shifting music.(59) However, this rhythmic device does not necessarily translate to the metrical domain. It has been argued that “no matter how complex it may be, . . . African rhythm always has a simple ultimate reference: the pulsation . . . whose function is similar to that of the Medieval tactus” (Arom 1991, 206), while mixed metrical structures “seem virtually nonexistent” (Temperley 2000, 70).(60) There is less evidence for rotation as an important musical device in repertoires with genuinely mixed metrical structures such as the traditional music of the Balkan regions.(61)
[6.6] If we were to establish a geometrical space for the similarity of rotationally equivalent meters, the mathematically intuitive approach would be to measure the degrees of rotation necessary to convert one meter into the other.(62) By that reckoning, 2223 is one “step” away from 2232, but two steps (and thus further) from 2322. Clearly this is a relevant compositional device; however, it is by no means the only way of assessing similarity among rotationally equivalent meters. Indeed, it fails to account for apparently important aspects of the musical experience. For instance, it considers first and last beats to be just as “neighboring” as other consecutive beats, and includes no acknowledgement of higher-level metrical structure.
Figure 19. Hypermetrical ambiguity in Bartók’s Concerto for Orchestra (movement IV, mm. 5–8 with anacrusis, oboe part)
(click to enlarge and listen)
[6.7] An analogy with tonal harmony is useful in illustrating this disconnect between proximity and similarity. Modulation by the incremental step of a semitone represents a far more significant change of tonal area (pitch collection) than modulation by the much larger intervallic distance of a fourth or a fifth. This is why graphical models of “closely related” keys (such as the circle of fifths or Schoenberg’s “Chart of the Regions”) exist. The order of importance among metrical positions appears to operate in a similar way. In a four-beat binary meter, beat positions 1 and 3 are more closely related to one another than to two and four due to nested, fractal, strong-weak alternations. In that sense, ((32)(22)) may be more closely related to ((22)(32)) than to ((23)(22)). For instance, in the opening oboe melody from the fourth movement of Bartók’s Concerto for Orchestra (shown in Figure 19), the hypermeter is ambiguous, and may be either ((32),(22)) or ((22)(32)), depending on the interpretation. The following section on “stability” addresses these issues in reference to empirical matters of perceptual preference and the (related) evidence of repertorial practice. These provide initial criteria for establishing a ‘meter metric’ based on relative stability.
Stability
[6.8] Among rotationally equivalent meters, some of the distinct rotations are far more commonly used in musical practice than others. For instance, (putting the rhythm-versus-meter debate to one side for the moment) it is telling to note that Pressing (Pressing 1983, 41) observes the conspicuous absence of the 23232 pattern from the Macedonian, Bulgarian, and African music he studied, in which all other rotations of that pattern are common.(63) He posits that the 23232 pattern may be avoided because it is the only rotation which neither starts nor ends with a 3. Similarly, musicians familiar with the Western canon will intuitively know how much rarer 232 is than the other rotations of {2,1}, 322 and 223.(64) There must be a reason for this extremely widespread, seemingly context-independent tendency; the greater usage might lead us to suppose that those forms are somehow more stable for perception and production by human musicians.
[6.9] The idea of a basic cognitive preference for particular rotations of rhythms and duration patterns as more “stable” than others has been empirically supported since at least Royer and Garner 1966.(65) Royer and Garner conclude that subjects select a rotation of a given pattern on two bases: a preference for beginning with the longest run of like elements (the “run” principle) and for ending with the longest gap (the “gap” principle). At least the “run” principle appears to be borne out in the musical practice discussed. In Toussaint’s ordering of “robust” rhythmic necklaces according their popularity, the most popular forms invariably begin with the longest run of like elements.(66)
[6.10] Some further support for the “gap” principle is offered by the well-known phenomenon of phrase-final lengthening, a concept borrowed from linguistics, which suggests that a temporal gap between recurring units such as measures is cognitively preferable—a kind of temporal articulation by delay of the strong beat.(67) According to this preference, meters with a longer final element may be described as “more natural” than their rotations. Parncutt has offered evidence suggesting that, although the longer IOI was sometimes preferred at the end of the run at slower tempos, “longer IOIs were perceived as more accented” at faster tempos (Parncutt 1994, 454). In short, there is strong evidence for the effect of durational accents on preferred metrical organization (Parncutt 1994, 426ff.), but the evidence does not seem to allow generalizations beyond a preference for articulating the start or end of a larger unit by positioning long and/or anomalous units there.(68) London (2012) also concludes that “About all that can be said regarding the preference for certain rotations is
[6.11] The notion of a “stable” metrical structure is also closely related to that of “maximal evenness” in pattern formation. The seminal study on this topic with respect to pitch is Clough and Douthett 1991; however, similar ideas have been applied to rhythm and meter. For Toussaint, the maximal evenness property is “most responsible for obtaining rhythms that are popular throughout the world” (2013, 131), and maximally even subdivision at each structural level is an explicit requirement in Meredith’s formalization of meter (1996, 214ff.).(69)
[6.12] Maximal evenness can be used to account for rotational preferences, though it is not without its pitfalls. In the meter {2,1}, the maximally even division of the 7-unit level into the standard three parts supports the well-formedness criteria of this meter vector; however, it does not express any preference for rotations of this meter. 232 is just as maximally even as 223 and 322 in this regard. Forcing a choice with respect to rotational preference requires an initial 2-part division of the meter (as in Meredith 1996, op. cit.). This successfully models the preference for 223 and 322 rotations (yielding maximally even 4+3 or 3+4 divisions) over that of 232 (which would be 5+2 or 2+5, which are not maximally even), but the two-part division into 2+1 beats is out of keeping with the well-formedness criteria for these meters. In this case, we apparently have to choose between maximal evenness as a criterion for rotational preference and the well-formedness criteria that are the core of the structural definition of our mixed meters.
[6.13] These conflicting criteria speak to more than just an isolated case. Problems are manifested in different ways for different meter vectors. For instance, maximal evenness requires that a 10-unit meter be divided into either five beat groups with duple subdivision (as in 5/4), or into two spans of five units, each of which must necessarily comprise a duple and a triple beat. This latter possibility leads to four rotations of the meter with vector {2,2} (2323, 3232, 2332, and 3223), but it excludes the two that remain (2233 and 3322) on the basis that they include a 4+6/6+4 grouping at the half-cycle level which is not maximally even. 2233 and 3322 orderings are comparatively rare meters, though perhaps no rarer than the maximally even 2332.(70)
[6.14] What is needed in order to organize all possible orderings, maximally even or otherwise, is a measure of relative evenness and stability. The hierarchy of the metrical structure is an obvious organizing principle. The higher the structural unit articulated by a long beat, the more stable it is, and the more similar it is to other meters formed in this way. Among the permutations of {3,1}, for instance, (22)(23) and (32)(22), may be considered more stable than (22)(32) and (23)(22) because in the former pair, the anomalous 3 beats occur at the start or end of the full cycle (i.e., the largest metrical unit, which may correspond to the measure).(71) This provides a basic formalization for an ordering preference and can be extended to meters of any cardinality.
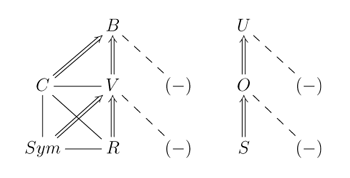
Symmetry (Sym)
[6.15] In proposing that meters with an anomalous beat that articulates either the start or end of a metrical unit are equivalent in terms of stability, we implicitly attribute a type of commonality to meters that are symmetrical to (metrical retrogrades of) one another.(72) Among {3,1} meters, for instance, (32)(22) and (22)(23) articulate the highest metrical level (the whole 9-unit cycle, which may correspond to the measure), while (23)(22) and (22)(32) articulate a lower level (the half-measure). These are both symmetrical pairs.
[6.16] Every meter is either symmetrically equivalent to exactly one other meter (such as 223 and 322), or it is internally symmetrical and forms no such pair (palindromic beat patterns like 232). Like rotational equivalence, symmetry is a restricted case of vector identity, and therefore also a restricted case of equivalent beat cardinality. No such entailment exists between symmetry and rotation: meters may be equivalent by rotation, symmetry, both, or neither. That said, symmetrical equivalence is a restricted case of rotational equivalence for meters of beat cardinalities < 6, and in practice this covers most meters in common-practice Western music at the least. For cardinalities ≥ 6, it is possible to construct four distinct beat successions that make symmetrical meters no longer rotationally equivalent. For instance, 332322 is not rotationally equivalent to its symmetrical pair 223233.
Figure 20. Symmetry in the metrical and motivic structure of Stravinsky’s Petrushka, reh. 15 mm. 1–4, 1947 version
(click to enlarge and listen)
[6.17] The symmetry relation may be significant or not depending on the musical context. In a passage from Stravinsky’s Petrushka, the beaming specifies that 23 and 32 forms of 5/8 alternate, and therefore that consecutive measures are symmetrical to one another, metrically. Symmetry is also evident in the patterning of material in the wind parts, reproduced in the upper staff of Figure 20. The four measures consist of an alternation between two chords (d and G) on repeated eighth notes, with two occurrences of each chord (excluding the first and last). The resulting motivic and metrical patterns are both symmetrical about the midpoint of each measure. For the metrical disposition, symmetry also holds between each successive measure.
[6.18] The chords in the strings, reproduced in the lower staff, articulate the start of each measure with another symmetrical pattern: a d–G–G–d (notwithstanding the viola part’s insistence on the D/E dyad throughout, which serves to link this passage to the preceding and following sections.) However, given their position at the start of each measure (on the downbeats), those string chords do not participate in the rhythmic symmetry of the upper parts, or at least not around the same axis. More systematic forms of this kind of temporal symmetry exist in the literature, for instance throughout Webern’s Symphonie op. 21. Even there, however, true symmetry of temporal pattern presupposes the “note” as an unvarying event and the termination of the note as equally important as the onset. This is deeply problematic given the importance of a note’s attack to its identity, let alone the inherent asymmetry of out temporal perception.(73) However, metrical symmetry may be more salient than rhythmic symmetry due to the relatively few permutations of metrical forms based on duple and triple grouping. This is likely to be especially true of passages in which occasional anomalous beats serve as referential markers in passages of predominantly one beat type (as in many repertoire examples discussed in this article). At the very least, this section introduces the metrical equivalent of a common motivic device, which is reason enough for inclusion in the analytical toolkit for meter.
Figure 21. Metrical symmetry in the Tanz from Orff’s Carmina Burana
(click to enlarge and listen)
[6.19] Metrical symmetry can, of course, be strongly articulated without any corresponding motivic symmetry, as in the Tanz of Carl Orff’s Carmina Burana, shown in Figure 21. The figure provides a reduction of the opening section of the piece (excluding the opening, introductory four bars): system 1 is followed by system 2 before a near-exact reprise of system 1. The two basic motives presented here, labeled A and B, fall at the start of each system. Their respective metrical structures of 4/4+3/8 (22223) and 3/8+4/4 (32222) are clearly articulated and are in an equally clear symmetrical relationship. Arrows indicate important metrical-motivic relationships; x, y, z, p, and q identify further parallels; and “+” indicates interpolations to the subsequent iterations of these prototypes.
Complementation (C)
[6.20] “Complementation” defines the relation between meters that have opposite beat types at all corresponding positions. Complementary meters necessarily have equivalent beat cardinality. They may also be vector-identical and even rotationally or symmetrically equivalent, but are not necessarily so; no entailments hold there. As with symmetry, each meter can have only one complement, but unlike the case of symmetry, it is not possible for a meter to complement itself.(74) Examples of complementary pairs of meters include 232 and 323, 2232 and 3323, and 2332 and 3223.
[6.21] This relation is designed primarily for mixed meters, but it also connects the duple and compound meters of each cardinality: 2 and 3, 22 and 33, 222 and 333, 2222 and 3333, and so on. The relation may hold for meters of any beat cardinality; however, it may be considered more significant for longer meters where the greater number of possible beat successions makes the complementation relation proportionately rarer. Complementary metric relationships are implicit in Figure 14, which is symmetrical with respect to complementation about its horizontal bisection (between meters 2332 and 3223).
Figure 22. Complementation between meters in two passages from Britten’s Rejoice in the Lamb
(click to enlarge and listen)
[6.22] The complement relation provides a useful framework for approaching the “con brio” section of Britten’s Rejoice in the Lamb from which two pertinent excerpts are reproduced in Figure 22. The passage is almost entirely based on an alternation between two contrasting ideas, one in loud mixed meter, the other in quiet compound meter (usually 6/8). The first juxtaposition of these ideas is shown as the first system of Figure 22. They are distinguished by the metrical disposition (here 7/8 versus 6/8), the melodic material, and the dynamic marking. This form of alternation proceeds throughout the section, and the 7/8 material appears in a variety of meters with a single triple beat that is invariably at the end of the measure: a prototypical 7/8 (223) as shown, followed by 9/8 (2223), 5/8 (23), and 11/8 (22223). All of these meters share the “Last” order relation. The metrical characterization of this material is very well established, as is the pattern of alternation.
[6.23] Towards the end of the section, the metrical situation is changed by swapping meters for their complements, as shown in the lower system. 4/8 appears for the first time, replacing 6/8 (see the third measure of the lower system, and compare especially the F–G–A–
[6.24] Both the term “complementation” and the associated mathematics require some comment concerning their relation to existing uses and formalisms. Firstly, the use of the term “complementation” differs from the group-theoretic definition employed in twelve-tone theory and in Pressing’s (1983) account of isomorphisms between rhythmic and scale structures.(75) Secondly, the formalism relates to two existing uses in the literature, one pertaining to a related consideration, the other not. Complementation is isomorphic in mathematical structure to Leong’s (2007) “vertical reflection” relation; however, Leong’s relation is designed to address proportional schemas in simple meters, and as such, the similarities reside in the mathematical formalism, and not in the musical comparisons.(76) The more musically relevant notion is the “contour” of a musical rhythm, based on the differences between the lengths of successive beats. As Toussaint observes, “humans have an easier time perceiving qualitative relations such as ‘less than’ or ‘greater than’ or ‘equal to’ than quantitative relations” (2013, 47). This distinction may easily be applied to meters and used specifically to formalize the complementation relation discussed here. For meters of two beat types (whether 2,3 or S,L), three contour types are needed to convey the length of the second in relation to the first: +, =, and −, representing beats that are longer, the same, and shorter.(77) For instance, 23223 may be described as (+,−,=,+). The complementation proposed here between 23223 and 32332 is neatly evident from their opposite patterns of durational contour: (+,−,=,+) and (−,+,=,−).
7. Summary and Illustration of Vector-Identical Order Relations (with Complementation)
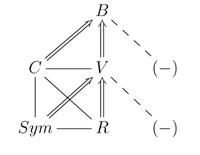
[7.1] The entailments among the relations just discussed—V (vector-identity), R (rotational equivalence), Sym (symmetry), and C (complementation)—may be summarized as follows:
- V, R, Sym, and C relations only hold among meters with equivalent beat cardinality; they all entail the B relation
- B-related meters may be vector-equivalent, complementary, both V and C, or neither
- R and Sym entail V
- any combination of R, Sym, and C may hold
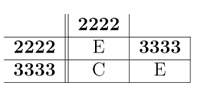
[7.2] These relations and their entailments are shown as a flowchart in Figure 23, which itself is contained within the summative Figure 24 at the end of this article. The set of examples for all meters of beat cardinality four will help to illustrate the structure of these relationships. The following tables set these out in three stages, for meter vectors {4,0} and {0,4} (shown in Table 1), {3,1} and {1,3} (Table 2), and {2,2} (Table 3).
Figure 23. The family entailments among the B, V, C, R, and Sym relations (click to enlarge) | Table 1. V, R, Sym, C (and E) relations among meter vectors {4,0} and {0,4} (click to enlarge) |
Table 2. V, R, Sym, C (and E) relations among orderings of meter vectors {3,1} and {1,3}
(click to enlarge)
Table 3. V, R, Sym, C (and E) relations among orderings of meter vector {2,2}
(click to enlarge)
[7.3] The relationships between {4,0} and {0,4}, as shown in Table 1, is simple. The two meters are complementary, each is symmetrical within itself, and each also has only one distinct rotation.
[7.4] Table 2 shows the meters {3,1} and {1,3}, and how R and Sym hold within each meter vector (notice the diagonal lines from top right to bottom left on which Sym holds), while the complementary relations hold between them. The meters {3,1} and {1,3} each have only one distinct permutation, with four rotations. Each of the four rotations for one meter is complementary to one of the other’s rotations (this is shown by another diagonal from top right to bottom left.
[7.5] Finally, as shown in Table 3, {2,2} might be viewed as a collapsed form of {3,1} and {1,3} in that the complement relation exists within the same meter vector (now on the same top-right-to-bottom-left diagonal as that of symmetry). Notice that 2332 and 3223 are only complementary and not also symmetrical to one another because they are each internally symmetrical (and thus have no symmetrical paired meter). As there are two beats of each type, R can no longer be assumed, so many of the pairs of meters shown here are related by V only.
8. Conclusions
Figure 24. The combined family structure of entailments for most of the metrical relations discussed
(click to enlarge)
[8.1] This study has provided a taxonomy and characterization of various relations that may hold among meters, especially mixed meters. Many relationships, terms, and ideas have been introduced, and so a summary is provided in this concluding section. The section begins with a glossary of the relations in the order they were mentioned, followed by a graphical summary of the family structure of their entailments (Figure 24).
- Grouping commonalities
- “E”: Equivalence. “Equivalent” meters can be expressed by the same formal structure. The relation is most significant where the corresponding levels align with respect to tempo and / or duration (see “Identity,” below). Where the structural parallel connects different levels, the relation may assume musical relevance through devices such as augmentation, diminution, and similar techniques. See Figure 4.
- “I”: Identity. Meters have the same metrical structure, and the corresponding levels align with respect to tempo and/or duration. See Figure 3.
- “G”: Partial Grouping Commonality. Meters share a partial structural identity but do not meet the criteria for equivalence or beat cardinality (below). G is rarely a significant relation because some commonality is almost inevitable given the narrow range of grouping options within the bounds of well-formedness.
- Cardinality relations
- “P”: Sub-Tactus Pulse Cardinality. Sub-tactus pulse cardinality holds among meters with the same number of units at the level below the tactus beat, whatever the structure of metrical grouping at other levels. For instance, 2223 and 333 each have 9 pulse units, but different higher-level groupings. Even similar pulse cardinalities can be musically significant, whether or not beat cardinality equivalence is also preserved (see Figure 5).
- “B”: Beat Cardinality. Meters have the same number of units at the counting or tactus level. See Figure 6. B is entailed by many other relations: V, C, R and Sym.
- “U”: Unordered Sub-/Super-Set. In the U relation, one meter has fewer of one beat type than the other, and a lesser or equal number of the other beat type (see Figure 7). This relation provides a connection between meters with similar vectors, but no significant commonality of ordering. It may assume significance for shorter meters, where there is a greater likelihood of listeners remembering the full vector content without the assistance of order relations. U is also entailed by O and S relations, but clearly B and U may not both concurrently hold.
- Order Relations
- “S”: Saturation. A longer meter (with more beats) may be fully expressed by successive instances of a shorter one. For instance, (23)(23) is saturated by two instances of 23. Where the multiplier corresponds to the hypermetrical structure of the shorter meter, the two meters are formally equivalent. See Figure 10. S entails O (which entails U).
- “O”: Non-Saturated Order Relations. A longer meter’s beat pattern contains within it the pattern of the shorter, without necessarily being saturated by it (see Figure 14). Three types of O relation are distinguished according to the position of the shorter meter within the longer—at the start (F), end (L), or within (W). For instance, 23 is L-related to 2223. Significance may be drawn from the number of beats held in common (a longer common string makes a stronger claim), from the nesting structure (where the smaller meter articulates a complete structural unit of the larger meter, even where saturation is not possible), and from the rarity of the pattern (order relations are trivial among meters with only one beat type). O entails U.
- Vector-Identical Relations and Complementation
- “V”: Vector Identity. Meters have the same number of each beat type but may differ in other respects such as beat ordering and higher-level groupings. Refer to Figure 2 for lists of meters by their vectors. V entails B.
- “R”: Rotation. Meters may share the same ordered pattern of beats but take a different starting point on that cycle (indeed, in aurally transmitted music, the starting point of a regular cycle may not be obvious). For instance, 322 is rotationally equivalent to 232 and 223. Clearly this is only of interest for mixed meters (which use both beat types); the concept of “ordering” is irrelevant to simple meters. R entails V (which entails B). R cannot be assumed of V meters with more than two of each beat type. The notion of stability in ordering was discussed in the context of rotation. Meters may be considered more stable—and similar to each other in that respect—where anomalous beats articulate large structural levels.
- “Sym”: Symmetry. Symmetry holds among pairs of meters for which the order of beats in one may be reversed to form the other. See Figures 20 and 21 for examples. All meters are symmetrical to either one other meter (pairs such as 23 and 32) or to none (internally symmetrical meters such as 2332). Sym entails V (which entails B). Sym and R may both hold. Indeed, for < 6 beats (which covers most of the meters in common usage), Sym entails R. However, for ≥ 6 beats, there may be four distinct beat successions, in which case Sym does not entail R.
- “C”: Complementation. Pairs of complementary meters (such as 23223 and 32332) have opposite beat types at every corresponding position. This also means that they have opposing “contour” patterns of beat-type changes: (+,−,=,+) versus (−,+,=,−) in this instance. See Figure 22. C entails B.
[8.2] As this summary reiterates, several of the relations entail others. For example, if two relations are rotationally equivalent (R), then they necessarily also have the same meter vector (V), and thus also the same number of beats (B). Figure 24 sets out this family structure of entailments for as many of the relations discussed as possible: B, V, C, R, Sym, and U, O, S. Note that these relations fall into two separate sets of entailments, as meters may not be both B- and U-related (see Figure 7). They may be B-related, U-related, or neither (there are pairs of meters for which none of these relations hold).
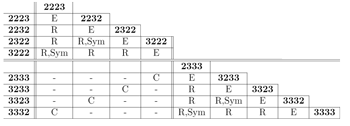
Table 4. Summary of relations among meters {1,0} to{0,3} including B, P, S, O, U, R, Sym, and C
(click to enlarge)
[8.3] Given those entailments, some meters are clearly rarer than others. To that effect, Table 4 sets out the rarest relation(s) to hold between the first few meters: {1,0} to {0,3}. Entailments that are implied by other relations are not included. For instance, in cases where R, C, or Sym hold, B is not also listed, as it is entailed by them.
[8.4] That said, any relation may assume significance in a particular musical context, however common it may be, and any combination of relations may be individually significant, whatever the nature of their entailments. It is therefore important to note that the relationships presented here all describe musically and intellectually separate classes of commonality between metrical structures. This conforms to David Lewin’s claim that “we do not really have one intuition of something called ‘musical space.’ Instead, we intuit several or many musical spaces at once” (1987, 250).(78) Partly for that reason, I do not provide an abstract hierarchy of importance among the relations. Those decisions are too contextually contingent to be generalizable, and are much better left to the analyst.(79)
[8.5] This ties in with the present study’s methodology of setting out metrical relations in separate mathematical spaces. These have been designed to provide the clearest possible visualization and conceptualization aids for the relations in question. Nevertheless, it is possible to construct a single, connected, three-dimensional space on which all meters have their place and in which all relations can be set out. As the spaces for the individual relations have helped to illuminate important aspects of the relations, I conclude by offering this summative space as well, in the hope that it will facilitate ongoing research in this area.
[8.6] Figure 25 sets out the beginning of this recursive space. Essentially, the structure combines the order relations of Figure 14 with the unordered relations of Figure 7. Here, the two-dimensional meter vector grid of Figure 7 provides the base, with the permutations of each vector set out on a third dimension (shown in the order used throughout this study). This continues to connect mathematical relations with musical ones: for instance, beat cardinality continues to hold on parallel cross-sections of the space (cf. Figure 7), and the space has (mathematical) rotational symmetry with respect to (musical) complementation about a central plane that bisects each vector list.
Figure 25. A connected, summative three-dimensional space for meters and metrical relations (click to enlarge) | Figure 26. An example using the space set out in Figure 25 for meter 2233, and the relations it shares with other meters of cardinality 1–4 (in red) (click to enlarge) |
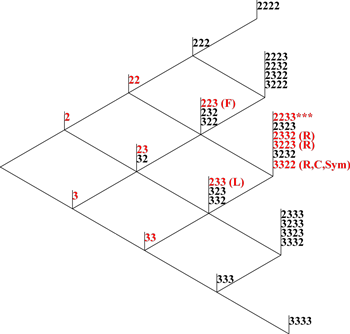
[8.7] Figure 26 provides an example that uses this three-dimensional space to illuminate one meter’s many connections. The example used (2233) is marked by asterisks, and the meters of cardinality 1–4 to which it is connected are shown in red. Naturally, R-, Sym-, and C-related meters all fall along the same (vector-equivalent) vertical, while the ordered subsets are in lower-cardinality-columns to the left. In this case, the F-relation consistently appears on the upper diagonal, and the L-relation on the lower diagonal (though this does not generalize to all meters—cf. Figure 14).
[8.8] The space and the example both reinforce recurring observations of this study. The example illustrated in Figure 26 illuminates the fact that order relations between neighboring cardinalities are more significant (rarer) than those between non-adjacent cardinalities. In the example given, just two out of the eight 3-beat meters are ordered subsets of 2233, while two of the three 2-beat meters and both of the 1-beat meters are.
[8.9] The space itself reinforces the observation that the “maximally mixed” meters (comprising the most equal sharing of beat types) are the most connected in terms of several relations. As in Figure 7’s two-dimensional space for the B and U relations, the center of Figure 25’s more comprehensive three-dimensional space (containing those “maximally mixed” meters) is the most populus and connected part, while the simple meters at the extremes have far fewer connections. This fact alone neatly encapsulates the motivation for the present study of relations among mixed meters.
Mark Gotham
University of Cambridge
Faculty of Music
11 West Road
Cambrdige, CB3 9DP, UK
mrhg2@cam.ac.uk
Works Cited
Amiot, Emmanuel, and Gillis Baroin. 2015. “Old and New Isometries between Pc-Sets in the Planet-4D Model.” Music Theory Online, forthcoming.
Arom, Simha. 1991. African Polyphony and Polyrhythm: Musical Structure and Methodology. Cambridge University Press.
—————. 2004. “L’aksak: Principes et Typologie.” Cahiers de musiques traditionnelles 17: 11–48.
Babbitt, Milton. 1962. “Twelve-Tone Rhythmic Structure and the Electronic Medium.” Perspectives of New Music 1, no. 1: 49–79.
Bartók, Béla. 1981. Hungarian Folk Song, ed. Benjamin Suchoff, trans. Michel D. Calvocoressi, annotated by Zoltán Kodály. State University of New York Press.
—————. 1992. Bela Bartók Essays, ed. Benjamin Suchoff. University of Nebraska Press.
Berger, Anna. 2002. “The Evolution of Rhythmic Notation.” In Cambridge History of Western Music Theory, ed. Thomas Christensen, 628–56. Cambridge University Press.
Benadon, Fernando. 2009. “Time Warps in Early Jazz,” Music Theory Spectrum 31, no. 1.
Bernstein, Leonard. 1976. The Unanswered Question: Six Talks at Harvard. Harvard University Press.
Brǎiloiu, Constantin. 1951. “Le rythme Aksak.” Revue de Musicologie 33, nos. 99 and 100: 71–108.
—————. 1984. Problems of Ethnomusicology. Cambridge University Press.
Christensen, Thomas, ed. 2002. Cambridge History of Western Music Theory. Cambridge University Press.
Cler, Jérôme. 1994. “Pour une théorie de l’Aksak.” Revue de Musicologie 80, no. 2: 181–210.
Clough, John and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35, nos. 1–2: 93–173.
Cohn, Richard. 1992. “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-shifting Music.” Perspectives of New Music 30, no. 2: 146–177.
—————. 1999. “As Wonderful as Star Clusters: Instruments for Gazing at Tonality in Schubert.” 19th-Century Music 22, no. 3: 213–32.
—————. 2001. “Complex Hemiolas, Ski-hill Graphs and Metric Spaces.” Music Analysis 20, no. 3: 295–326.
—————. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. Oxford University Press.
Cooper, Grosvenor and Leonard Meyer. 1960. The Rhythmic Structure of Music. University of Chicago Press.
Cross, Ian. 1997. “Pitch Schemata.” In Perception and Cognition of Music, ed. I. Deliège and J. Sloboda, 357–90. Hove.
Djoudjeff, Stoyan. 1931. Rythme et mesure dans la musique populaire bulgare. Champion.
Dunsby, Jonathan. 1994. “Criteria of Correctness in Music Theory and Analysis.” In Theory, Analysis and Meaning in Music, ed. Anthony Pople, 77–85. Cambridge University Press.
Forth, James. 2012. “Cognitively-Motivated Geometric Methods of Pattern Discovery and Models of Similarity in Music.” PhD diss., University of London.
Gilles, André and Gilbert Reaney. 1966. Torkesey, Declaratio Trianguli et Scuti, no. 12 in “Corpus Scriptorum de Musica.” American Institute of Musicology.
Gotham, Mark. 2015. “Attractor Tempos for Metrical Structures.” Journal of Mathematics and Music 9, no. 1: 23–44.
Hasty, Christopher. 1997. Meter as Rhythm. Oxford University Press.
Heinichen, Johann. 1711. Neu erfundene und gründliche Anweisung—zu vollkommener Erlernung des General-Basses, Schiller.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press.
Iyer, Vijay. 2002. “Embodied Mind, Situated Cognition, and Expressive Microtiming in African-American Music.” Music Perception 19, no. 3: 387–414.
Kirnberger, Johann Philipp. 1982 [1779]. The Art of Strict Musical Composition, trans. David Beach and Jürgen Thym. Yale University Press.
Kubik, Gerhard. 1999. Africa and the Blues. University Press of Mississippi.
Kvifte, Tellef. 2007. “Categories and Timing: On the Perception of Meter.” Ethnomusicology 51, no. 1: 64–84.
Lau, Wing. 2015. “Composing Declamation: Notated Meter Change in Brahms’s Lieder.” Music Theory Online 21, no. 2.
Leong, Daphne. 2007. “Humperdinck and Wagner: Metric States, Symmetries, and Systems.” Journal of Music Theory 51, no. 2: 211–43.
Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Lewin, David. 1981. “On Harmony and Meter in Brahms’s op. 76, no. 8.” 19th-Century Music 4, no. 3: 261–65.
—————. 1984. “On Formal Intervals Between Time-Spans.” Music Perception 1, no. 4: 414–23.
—————. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
Locke, David. 1998. Drum Gahu: An Introduction to African Rhythm. White Cliffs Media.
London, Justin. 2002. “Some Non-Isomorphisms between Pitch and Time.” Journal of Music Theory 46, nos. 1–2: 127–51.
—————. 2012. Hearing in Time: Psychological Aspects of Musical Meter, 2nd ed. Oxford University Press.
Longuet-Higgins, Christopher and Christopher Lee. 1984. “The Rhythmic Interpretation of Monophonic Music.” Music Perception 1, no. 4: 424–41.
McCandless, Greg. 2013. “Metal as a Gradual Process: Additive Rhythmic Structures in the Music of Dream Theater.” Music Theory Online 19, no. 2.
Meredith, David. 1996. “The Logical Structure of an Algorithmic Theory of Tonal Music.” PhD diss., University of Oxford.
Messiaen, Olivier. 1956. Technique de mon langage musical. Alphonse Leduc,
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791. Oxford University Press.
Moelants, Dirk. 2006. “Perception and Performance of Aksak Metres.” Musicae Scientiae 10, no. 2: 147–172.
Murphy, Scott. 2009. “Metric Cubes in Some Music of Brahms.” Journal of Music Theory 53, no. 1: 1– 56.
Oettingen, Arthur. 1866. Harmoniesystem in Dualer Entwicklung. W. Gläser.
Parncutt, Richard. 1994. “A Perceptual Model of Pulse Salience and Metrical Accent in Musical Rhythms.” Music Perception 11, no. 4: 409–64.
Polak, Rainer and Justin London. 2014. “Timing and Meter in Mande Drumming from Mali.” Music Theory Online 20, no. 1.
Povel, Dirk-Jan and Peter Essens. 1985. “Perception of Temporal Patterns.” Music Perception 2, no. 4: 411–40.
Pressing, Jeff. 1983. “Cognitive Isomorphisms Between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonality.” Studies in Music 17: 38–61.
Rahn, Jay. 1986. “Asymmetrical Ostinatos in Sub-Saharan Music.” In Theory Only 9, no. 7: 23–37.
—————. 1996. “Turning the Analysis Around: Africa-Derived Rhythms and Europe-Derived Music Theory.” Black Music Research Journal 16, no. 1: 71–89.
Rice, Tim. 2000. “Bartók and Bulgarian Rhythm.” In Bartók Perspectives: Man, Composer, and Ethnomusicologist, ed. Elliott Antokoletz, Victoria Fischer, and Benjamin Suchoff, 196–212. Oxford University Press.
Rings, Steven. 2011. Tonality and Transformation. Oxford University Press.
Roeder, John. 2003. “Beat-Class Modulation in Steve Reich’s Music.” Music Theory Spectrum 25, no. 2: 275–304.
Royer, Fred and Wendell Garner. 1966. “Response Uncertainty and Perceptual Difficulty of Auditory Temporal Patterns.” Perception and Psychophysics 1: 41–47.
Temperley, David. 2000. “Meter and Grouping in African Music: A View from Music Theory.” Ethnomusicology 44, no. 1: 65–96.
Todd, Neil. 1985. “A Model of Expressive Timing in Tonal Music.’ Music Perception 3, no. 1: 33–57
Toussaint, Godfried. 2013. The Geometry of Musical Rhythm. Taylor and Francis.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. Yale University Press.
Zuckerkandl, Victor. 1956. Sound and Symbol: Music and the External World. Routledge.
Footnotes
1. This meaning of “mixed” is not to be confused with other uses of that term in the literature such as Cohn’s (2001) “mixed” combinations of 2- and 3-groupings at different levels of the same metrical structure. Conflicting uses of this kind are unfortunate, but are to be expected of such general terms. The term “mixed meter” is used here in spite of that shortcoming, as it is both the most technically descriptive and value-neutral term in common use. Other terms used for the same subject include “complex meters” (which is even worse for multiple, conflicting meanings and also less descriptive of the subject), “non-isochronous meters” (which now also stands for more kinds of non-isochrony than the formally different beat types—see Table 7.1 of Polak and London 2014 for a summary), and “Aksak meters” (which has stylistic connotations specific to a particular repertoire).
Return to text
2. See especially Cooper and Meyer 1960, Yeston 1976, Lerdahl and Jackendoff 1983, and London 2012.
Return to text
3. Those lists tend to be found in primarily ethnographic studies. See Arom 2004, Cler 1994, and Brǎiloiu 1984 and 1951 for examples dedicated to Aksak music. For comparable lists of asymmetrical rhythmic timelines in African music, see also Rahn 1986 and Toussaint 2013, though note that these asymmetrical rhythms are not the same as mixed meters. This distinction is discussed further below.
Return to text
4. This kind of harmony-to-meter analogy has also been made in other ways. Perhaps most relevantly, Lewin’s (1981) analysis of the Brahms Capriccio, op. 76, no. 8, connects and analogizes certain hemiola relations to the harmonic categories of dominant and subdominant functions. However, Lewin never developed more comprehensive metrical spaces, despite that promising analysis. The extensive formalization of distance measurements in his magnum opus, Generalized Musical Intervals and Transformations (1987), does include some account of temporal matters, though not distance between meters. See also Lewin 1984 for a related article dedicated to formalizing time-spans. Conversely, see London 2002, which argues against such analogies.
Return to text
5. Strictly speaking, this is a one-dimensional circle in a two-dimensional plane.
Return to text
6. See Heinichen 1711, Oettingen 1866, Cohn 1999, and Tymoczko 2011 for examples of each. Four-dimensional pitch-class space is also modeled in Amiot and Baroin (2015). Relevant articles in the Cambridge History of Western Music Theory (Christensen 2002) provide an historical survey, and Cross (1997) describes further models and uses in the late twentieth-century literature on music cognition.
Return to text
7. That said, there are patently mixed metrical passages among Brahms’s output. For instance, see the Andante Grazioso of the op. 101 C-minor piano trio, in which 3/4 alternates consistently with two 2/4s (=7/4) at the start, and later 9/8 alternates with 6/8 (=15/8). See also Lau (2015) in this issue, which discusses the mixed meters in Brahms’s songs “Agnes,” op. 59, no. 5, and “Das Mädchen,” op. 95, no. 1.
Return to text
8. Cohn comes to similar conclusions with reference to the “Cube dance” and Tonnetz as “modes for representing triadic progressions” (Cohn 2012, 89). Both can accommodate the necessary range of relations described; however, each is better suited to a narrower range of relations among the set.
Return to text
9. This makes the theoretical apparatus ill-suited to repertoires such as the Norwegian springar, a folk dance in which a continuum of sub-divisional proportions appears to be used without recourse to consistent classes of categorical division (see Kvifte 2007, especially Figure 3 on p. 71). But mixed meter is not a part of that musical language anyway (higher levels tend to be isochronous).
Return to text
10. The limitation to grouping by twos and threes excludes the use of a single-element span as a metrical duration on more than one structural level. This is how Stravinsky notates passages in the finale of Dumbarton Oaks, for instance. The relationships in this study can account for those meters only insofar as the single-unit span may be considered a separate meter (such as 3/4 + 1/8 instead of (2+2+2+1)/8, for instance). This is compatible with related notations such as that used in the second movement of Lutosławski’s Concerto for Orchestra in which single 1/4 bars break up the flow of a predominant 3/4 (at fast tempo). See London’s well-formedness criteria on this matter (2012, 91ff., especially WFC 3.4).
Return to text
11. It is best to avoid the term “beat class,” which is used in the music theory literature as a rhythmic analogy to “pitch class,” which denotes a metrical position; see Babbitt 1962, Cohn 1992, and Roeder 2003.
Return to text
12. See Moelants 2006, 153. It is also important for meters with a non-CFP subdivision of the beat, such as swing music (see the discussion in Polak and London 2014, section 7.4), but this is not the focus of the present study.
Return to text
13. “Establishing a meter with three specific beat classes is a perceptually difficult task, as various constraints lead one to reduce the three beat-classes to two” (London 2012, 135).
Return to text
14. Compare, for instance, the different representations of meter by Zuckerkandl 1956, Cooper and Meyer 1960, Bernstein 1976, Lerdahl and Jackendoff 1983, Hasty 1997, Cohn 2001, Murphy 2009, London 2012, and Toussaint 2013.
Return to text
15. To be absolutely clear, a “triple” beat consists of three units (in other words, it is 1.5 times the length of a duple beat). This differs from a “triple,” which implies 3-wise division of a beat in a predominantly duple context.
Return to text
16. Ordered meters are best represented by “ordered (plane), undirected trees,” or “arborescences,” in which there is exactly one path from each “leaf node” to each “root vertex.” See Forth 2012 for a mathematical definition of tree structures from first principles, and a (slightly different) application to musical meter (Forth 2012, sections 5.3.2 and 5.3.3, 108ff.).
Return to text
17. This mirrors some biases of Western notation (including the need for extra symbols to indicate triplets) and practice (in which binary grouping has been far more common since at least the ars nova). For a relevant history of early rhythmic notation, see Berger 2002. Even in meters of predominantly ternary grouping structures such as 9/8, in which the measure comprises three beats and the beat comprises three eighth notes, the eighth notes are assumed to divide into two sixteenths (not three). It is rare for a passage to sustain even three levels of “threeness.” The ritmo di tre battute section in the scherzo of Beethoven’s Ninth Symphony is one of few famous examples. It is written in 3/4, explicitly groups its measures in threes, and parts of the passage may be said to group those three-measure units into threes at the next hypermetrical level. Bach’s “Jesu Joy of Man’s Desiring” (“Jesus Bleibet Meine Freude” from Cantata BWV 147, Herz und Mund und Tat und Leben) is a less-oft cited example of a similar configuration. Measures 40–54 represent the longest consistent three-measure hypermeter. See Huron 2006 for further discussion of the binary default.
Return to text
18. Here, compound refers to meters with exclusively triple beats. Incidentally, this preference betrays a Western bias: in Bulgarian music mixed meters are much more common than ternary meters such as 3/4 (Rice 2000, 204).
Return to text
19. See, for instance, the discussion of the effect of metrical levels on tempo optimization in Gotham 2015.
Return to text
20. No parallels with standard mathematical usage should be assumed (such as curly brackets for listing elements in a set).
Return to text
21. Formalizations of (integer multiple) proportional structure between levels (such as Longuet-Higgins and Lee’s Lemma 3 [1984, 432]) exclude mixed meters by definition.
Return to text
22. As discussed, lists of mixed meters are not new, though some of the methods for representing these meters are.
Return to text
23. This sense of a “grouping structure” is not to be confused with Lerdahl and Jackendoff’s (1983) grouping structure of rhythms and phrases.
Return to text
24. Other examples of this exact notational convenience include Prokofiev’s Violin Concerto no. 1, in which the codas to first and third movements comprise exactly the same material expressed respectively in 6/8 and 3/4. Other examples of this relation between other pairs of meters include the final measures at the end of first and second movements of Rachmaninoff’s Third Symphony.
Return to text
25. Here the rotation is unclear—it could either be (23) or (32) as shown by the conflicting, out-of-phase brackets above and below the example. The treble part is suggestive of (23), especially given the position of note changes, while the bass riff implies (32), especially in the context of intervening versions of this material, such as that shown in 4b. The other ⟨5⟩ meters in this example are ambiguous with respect to grouping, though not to phase—indeed the clear phase of 4b has a strong bearing on how to parse 4a, suggesting the (32) option.
Return to text
26. Whether this 5/2 is really metrical is a separate question, as it occurs only once and corresponds to a very long “pulse” span. Note that the material corresponding to example 4d actually occurs immediately before that of 4c in the track. The function of 4d is ambiguous; it appears to be tension-building – perhaps preparing a chorus – though what follows is anti-climactic.
Return to text
27. Clearly, the E relation is liable to downplay the importance of metrical level usage, contrary to the spirit of the “attractor tempos” model of Gotham 2015 (as discussed above).
Return to text
28. For instance, ⟨10 5 2⟩, ⟨11 5 2⟩ and ⟨12 5 2⟩ share partial grouping commonality on the basis of their equivalent beat cardinality (discussed below).
Return to text
29. Formally, meters A {xa, ya} and B {xb, yb} share equivalent pulse cardinality if and only if 2(xa) + 3(ya) = 2(xb) + 3(yb). In the case of the Brubeck example, 2(3) + 3(1) = 2(0) + 3(3) = 9.
Return to text
30. The motive first appears at reh. 11 and also recurs three measures before reh. 14.
Return to text
31. See Messiaen 1956 on additive rhythm. Bartók discusses mixed meters in additive terms in many places. For instance, “5/8 can be explained as a doubling of one of the eighths in a 2/4, and 7/8 as a doubling of one of the eighths in a 3/4 measure” (Bartók 1992, 391–92). This idea has been addressed in other repertoires too; see McCandless (2013) for an account of additive rhythmic structures in the rather different context of the music of Dream Theater.
Return to text
32. Formally, equivalent beat cardinality holds between two meters {x1, y1} and {x2, y2} if and only if x1 + y1 = x2 + y2. That is, we sum the duple and triple beats in each meter and compare them.
Return to text
33. Engaging with repertoires outside of common-practice Western art music is a recurring consideration of this study. While some of the relations presented here may seem like abstract formalisms, many are primarily concerned with bypassing artifacts of notation and the transcription process and getting closer to essentially musical matters.
Return to text
34. Microtiming is a lively area of current research. For instance, in addition to Kvifte 2007 and Moelants 2006, discussed here, see also Benadon 2009, Iyer 2002, and Polak and London 2014.
Return to text
35. This was discussed above in relation to the Springar repertoire, where it could be argued that categories of sub-division do not even exist. The CFP criteria were necessary for the grouping and pulse cardinality relations, but it is not essential to beat cardinality or the relations discussed in subsequent sections. This is an extreme case, but ambiguous sub-division structures are not. Perhaps the most frequently discussed repertoire context is the “swung rhythm” that is widely regarded as being neither a triplet nor a dotted rhythm.
Return to text
36. “Bulgarians don’t keep an underlying pulse going as a way to keep them in the meter. They have internalized the 3-to-2 relationship” (Rice 2000, 203). See also Moelants 2006, 153.
Return to text
37. See Moelants 2006 for an extensive study in relation to the Aksak repertoire. Moelants uses the designations Q[uick] and S[low] (153). See also the discussion of perceptual limits in ch. 2 of London 2012, for instance.
Return to text
38. Formally, this is a lattice whose vertices are the integer points in the positive quadrant of the real plane.
Return to text
39. These metric shifts follow the implications of Tallis’s original, which is a great source of metrical interest in its own right.
Return to text
40. The consistent two-measure phrases are arguably contrary to the spirit of Tallis’s original.
Return to text
41. Formally, meter A {xa, ya} is an unordered subset of meter B {xb, yb} if xb ≥ xa and yb ≥ ya and either or both of xb > xa and yb > ya. This could be expressed more simply with only the first conditions (xb ≥ xa and yb ≥ ya), but it is desirable to eliminate the trivial case of the U relation that holds between a meter and itself, which is much better expressed by other relations.
Return to text
42. The number of unordered subsets in each case can be derived from the meter vector (or position in this vector space) by the equation (x + 1)(y + 1) − 2.
Return to text
43. Clearly the perception of structure at higher metric levels is a tempo-dependent consideration. A telling comparison is often raised between the second movement of Tchaikovsky’s Sixth Symphony, which is in 5/4 at quarter note = 144, making the tactus itself unequal, and the third movement of Chopin’s Piano Sonata op. 4, which is also in 5/4 but at half the speed, with quarter note = 72 and thus with consistent duple beats at the tactus level. See Bartók (Bartók 1992, 40 and Arom 2004, 11. Is it a coincidence that the Tchaikovsky is a frequently cited example of mixed meter in the nineteenth-century repertoire, while the much earlier Chopin example is almost never mentioned? Bartók limited that which he called the “Bulgarian rhythm” (which is really a “Bulgarian meter,” as Rice 2000 observes) to fast tempi.
Return to text
44. The eighteenth-century composer and theorist J. P. Kirnberger used the term “compound meter” in the same sense that “saturated superset” is used here, indicating large meters formed by combining smaller ones. For a modern translated edition, see Kirnberger 1982 [1779], 399. As the editors note, Kirnberger’s use of “compound meter” clearly does not correspond to the modern one. The relation is also (nearly) defined by Longuet-Higgins and Lee (1984) in the rather different context of attempting to formalize the parsing of meter from rhythm. The authors define one metrical interpretation of a given rhythm as being “implicit” in another if “all metrical units of the former are present in the latter” (434). The interpretation involving more metrical levels is described as “richer.”
Return to text
45. The lines of Figure 10 cross to bring together meters of the same pulse cardinality such as 3/2, 6/4, and 12/8.
Return to text
46. The literature on simple meters includes Cohn 2001, Leong 2007, and Murphy 2009 as discussed above, as well as London’s Zeitnetz (2002, 2012) and even the fourteenth-century triangle of Johannes Torkesey (see Gilles and Reaney 1966).
Return to text
47. To formalize the relationship, let a and b stand for two meters, expressed by an entry in the Order column of Figure 2 above. The saturation relationship holds between meters a and b if and only if there exists a natural number n such that meter a is equivalent to n consecutive forms of meter b.
Return to text
48. To formalize non-saturated order relations for any cardinality (respectively m and n such that m < n), let S1 = (x1, x2
- F(S1, S2) holds if and only if (x1 = y1),(x2 = y2) . . . ( xm = ym);
- L(S1, S2) holds if and only if (x1 = yn−m+1) . . . (xm−1 = yn−1), (xm = yn); and
- W(S1, S2) holds if and only if (x1 = yr) . . . (xm = yr+m−1) for all values of r such that 2 ≤ r ≤ n − m.
Return to text
49. For instance, (2) is F, W and L related to (2232), without the Saturation relation holding.
Return to text
50. A form of the W relation appears to be important in the rhythmic domain for patterns of West and Central African asymmetric timeline patterns which all share an internal structure. Kubik expresses this on a pyramidal chart, with the common elements vertically aligned in the center (Kubik 1999, 54).
Return to text
51. If α F β and β L γ then α W γ.
Return to text
52. Highlighting the commonalities between the start of a meter’s beat pattern (the First relation) also engages positively with theories of projection in meter. Durational and metric projection as an interpretive model has been championed recently in Hasty 1997—see chapter 8 for historical precedents including Friedrich Neumann—and Mirka 2009.
Return to text
53. Below, I discuss the preponderance of these rotations in the context of metrical “stability.”
Return to text
54. For instance, the passage from reh. 24 to 25 consists of two measures of 7/16 (223), followed by two of 9/16 (2223) and finally one of 11/16 (22223). A similar device in Britten’s Rejoice in the Lamb is discussed below in connection with the “Complementation” relation. Although the meter vector space set out in Figure 7 is unordered, relations like these may be usefully characterized in those terms. All meters with the kind of L relation discussed here lie along the second lowest row ({0,1}–{1,1}–{2,1} . . . ).
Return to text
55. “Rotational equivalence” is one of Pressing’s 1983 relations (applied to both scales and rhythms), and Toussaint uses the term “necklace” (from mathematical combinatorics) to describe the relation (2013, Chapter 14).
Return to text
56. The meters of this type for beat cardinalities 2, 3, and 4 are {1,1}, {2,1}, {1,2}, {3,1}, and {1,3}. Using “=” to mean “is rotationally equivalent to,” then the relations may be set out as follows: 23 = 32; 223 = 232 = 322; 233 = 323 = 332; 2223 = 2232 = 2322 = 3222; and 2333 = 3233 = 3323 = 3332.
Return to text
57. These aspects of rotational symmetry are the motivation for the circular representations of meter used by Toussaint 2013, for instance.
Return to text
58. See Pressing (1983), Locke (1998), and Toussaint (2013).
Return to text
59. See Cohn 1992 and Roeder 2003 for analytical models for phase-shifted music.
Return to text
60. I suggest that the litmus test for genuinely mixed metrical structures should be the use of timelines that are incommensurate with isochrony. Debates over mixed-metrical versus syncopated readings of a 323 pattern are all very well, but if the recurring cycle itself is seven units long, then the matter is settled.
Return to text
61. Polak and London 2014 take these to be two different types of mixed meters.
Return to text
62. Cf. the circular representations for rotational symmetry such as rhythm necklaces and pitch-class clock-face diagrams, as well as the “edit distance” in computer science, which quantifies how many steps are needed to transform one word into another.
Return to text
63. This is not to say that 23232 never occurs. Godfried Toussaint identifies 23232 as “a bell pattern used in the Dominican Republic as well as Morocco” (Toussaint 2013, Rotation 1 of Figure 14.7, 77–78). Indeed, Toussaint describes this necklace as “robust,” meaning that all of its rotations appear in musical cultures somewhere in the world. However, he too acknowledges that certain orderings of these ‘robust’ rhythms appear to be considerably more common than others.
Return to text
64. Again, this is not to suggest that 232 never occurs. Some examples of that meter used (or at least notated) in the twentieth-century repertoire are: Copland, Appalachian Spring, reh. 11 m. 2 (Fig. 5) and reh. 12 m. 9; Bartók, Concerto for Orchestra, movement IV, m. 47 and equivalent moments (mm. 54 and 124); Dallapiccola, Variations for Orchestra, m. 6; Stravinsky, Petrushka (the initial form of the septuplet rhythms between reh. 3 and 5 in the 1947 version is 232; this idea recurs but is consistently “resolved” to 322 and other simpler forms); Duruflé, “Lux Aeterna” from the Requiem (both 322 and 232 forms of 7/8 occur); Duruflé, Messe Cum Jubilo (a single occurrence of 232 in the Gloria at reh. 10); Walton, “Chichester” Canticles, Magnificat, m. 21; Reich, Proverb (the 232 ordering of 7/8 is used as often as the more standard 322).
Return to text
65. Povel and Essens 1985 is a landmark study among subsequent work on this topic.
Return to text
66. Toussaint cites one rhythm of each beat cardinality: 332, 2223, 22323, 221221.
Return to text
67. See also Todd 1985.
Return to text
68. There is evidence for tempos and section lengths as an important consideration for ordering in musical practice. In the context of an Eastern Turkish dance-based repertoire, Cler 1994 discusses ordering norms specific to the tempo of the dance as well as to the number of repeated measures in a unit.
Return to text
69. See also Rahn 1996.
Return to text
70. For instance, the first movement of Bartók’s Music for Strings, Percussion and Celesta contains four instances of 10/8: 3232 (weakly articulated in m. 21); 3322 in most of the parts in m. 41; 2233 in m. 44; and finally 3223 in m. 79. Only two of these patterns are “maximally even.” In the “Lux Aeterna” of Duruflé’s Requiem, 10/8 appears twice in the solo organ passages, both times explicitly as 3322.
Return to text
71. This ordering principle can apply just as easily to hypermetrical structure. For instance, the 2233 and 3322 patterns discussed can result from the alternation of 2/4 and 6/8 meters. These notational arrangements are common in the repertoire. Among several of the works already discussed, a hypermetrical {3,1} is created through the alternation of 2/x and 5/2x time signatures. In Bartók’s Music for Strings, Percussion and Celesta, mm. 264–79 consistently alternate between 2/4 and 5/8 (23), resulting in a stable hypermetrical 2223. A less stable 2232 hypermetrical structure emerges in Copland’s Appalachian Spring at reh. 31 mm. 1–12. In both relatively extended passages, the alternation resolves initially to a consistent 5/8 rather than 2/4, perhaps because the composers desired a more gradual step than a total resolution to simple meter. Cf. also the pairing of 23 and 2223 in the example from Djoudjeff 1931, shown here as Figure 16. Of course, there is no shortage of counterexamples. For instance, the 2322 measures in Stravinsky’s Dumbarton Oaks (5/16+2/8, reh. 3 m. 3 and reh. 5 m. 3) appear among predominantly simple meters (2/4, 3/4, 4/4).
Return to text
72. The “symmetry” relations discussed here concern beat ordering in mixed meters, an entirely separate consideration from the “symmetry” relations in the literature on simple meters (such as Leong’s [2007] “r180” relation and Gotham 2015). In future work that uses these two types of symmetry concurrently, it may be desirable to distinguish an “O[rder]-Sym” (for beat ordering) from a “P[roportional]-Sym” for proportional schemes.
Return to text
73. Povel and Essens 1985 refers to the literature disproving the perceptual importance of temporal symmetry: “Mach (1886) pointed out that symmetry is not perceived in the case of temporal patterns, a finding later confirmed by Restle (1976)” (Povel and Essens 1985, 412). Symmetry is also implicitly undermined by projective accounts of musical meter such as Hasty 1997.
Return to text
74. Complementarity holds among meters with complementary meter vectors. That is, {x1, y1} and {x2, y2} may be complementary if and only if x1 = y2 and y1 = x2.
Return to text
75. The kind of complementation described by Pressing, based on figure-ground reversal (after Gestalt psychology), applies to rhythms but not to meters in which only two- and three-beat units are permitted, because the complement of any pattern with a 3-unit necessarily contains a 1-unit. Although patterns such as 2212221 can easily be conceived in terms of mixed meters (here 23223 is surely the most natural), this is contrary to the spirit of the exercise. The two senses can be made commensurable but only rather artificially.
Return to text
76. This mathematical isomorphism but musical divergence is also true of Leong’s “r180” relation and the symmetry relation discussed above.
Return to text
77. This system could be applied to structures in which more than two beat types are used. The number of comparisons (Comp) is given by the number of beat types used (n). Comp = 2n − 1.
Return to text
78. This is a philosophy that lies behind much subsequent work that builds on Lewin’s legacy, including Rings 2011.
Return to text
79. Some scholars do commit to one type of metrical change being basically more or less disruptive than another. For instance, Murphy claims that changes on two structural levels invoke “a stronger sense of alteration” than the loss of equivalent measure duration (2009, 13)—which is to say that 6/8 is closer to 9/8 than 3/4, for instance.
Return to text
- F(S1, S2) holds if and only if (x1 = y1),(x2 = y2) . . . ( xm = ym);
- L(S1, S2) holds if and only if (x1 = yn−m+1) . . . (xm−1 = yn−1), (xm = yn); and
- W(S1, S2) holds if and only if (x1 = yr) . . . (xm = yr+m−1) for all values of r such that 2 ≤ r ≤ n − m.
Copyright Statement
Copyright © 2015 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
16540