Hipster Harmony: The Hybrid Syntax of Seventh Chords in Post-Millennial Rock
David J. Heetderks
KEYWORDS: chromaticism, rock, art rock, experimental rock, experimental pop, progressive rock, Dirty Projectors, Radiohead, Mew, Grizzly Bear, Deerhunter, musical geometry, seventh chords, transformational theory, chromatic harmony
ABSTRACT: This article argues that art-rock groups active since 2000 often use chromatic progressions between seventh chords and other chords of four or more notes in order to differentiate themselves from generic rock styles. These groups introduce chromatic progressions through one of three schemas: altering a recurring diatonic progression (a recurring Roman-numeral progression), exploring the voice-leading possibilities of a recurring chord (a magic chord), and exploring the diatonic and chromatic possibilities of a voice-leading motion (a magic voice leading). When a chromatic progression appears, it functions as a large-scale, tonally undetermined alternation between two chords, or as a substitution for a normative progression. Hybrid syntax occurs where progressions arising from the techniques listed above are juxtaposed with common rock progressions. I analyze instances of hybrid syntax in songs by Dirty Projectors, Deerhunter, Mew, Grizzly Bear, and Radiohead. In these songs, chromatic progressions conspire with lyrics, timbre, and texture to convey otherworldliness or ambiguity, supporting the depictions of unusual personae or situations that art-rock groups favor.
Copyright © 2015 Society for Music Theory
Introduction
[0.1] Many rock critics recognize that a broad genre of rock music has emerged since around 2000. Often labeled “art rock” or a similar term such as “experimental pop,”(1) this genre is characterized by unusual timbres often incorporating high vocals, combination of sounds from a broad array of styles, and projection of a progressive ethos through means other than overt displays of virtuosity (Osborn 2010, 54–56). Representative bands include Animal Collective, Dirty Projectors, Mew, Radiohead, and St. Vincent. Other bands, such as Deerhunter, Grizzly Bear, and Tame Impala, are sometimes assigned related labels such as “chamber pop” or “neo-psychedelic”; their music nonetheless displays similar characteristics.(2) Music critics writing about art-rock bands often note the complexity or intricacy of their textures, using descriptors that range from “lush and opulent” to “difficult and cerebral.”(3) This textural intricacy places the genre in the legacy of 1990s indie rock, which, as David Blake points out, uses timbral heterogeneity as a primary means of expressing differentiation from the musical mainstream (2012, [8.4]).(4) In addition, while art-rock artists sometimes engage in formal experimentation, unlike neo-progressive bands, they tend to write concise songs. Critical circles that favor art rock, such as the well-known music criticism website Pitchfork.com, praise the artists’ autonomy from the mainstream, presentation of a unique or ambiguous lyrical persona, and meticulous craft. The positive appraisal of these characteristics is evident from Pitchfork’s numerical ratings: with a few exceptions, the site gave each of the albums containing the songs discussed in this article a rating of 9.0/10 or higher.(5)
[0.2] This article explores another facet of post-millennial art rock that has received little analytical attention: chromatic experimentation. Not all art-rock bands explore unusual chromatic harmonies, and some do so only infrequently, but there are enough striking examples to consider chromaticism a feature of the genre. Chromaticism helps art-rock bands assert a progressive ethos that distinguishes them from contemporaneous generic rock styles, and it links them to earlier styles that engaged in similar experimentation. This article thus complements studies of chromaticism in other rock styles by Capuzzo (2004), Everett (1997, 2008, 2012), Harrison (1997), Holm-Hudson (2008, 2010), Kochavi (2002), Reale (2014), and others.
[0.3] Previous studies of chromaticism in rock music largely use the interpretive lens of tonal function,(6) or they adapt labels from neo-Riemannian theory, focusing on parsimonious voice leading among triads.(7) By contrast, many art-rock bands use chromatic progressions involving thicker chords that contain four or more notes. Their music is thus a proving ground for exploring chromatic voice-leading relations among seventh chords, and it allows for an expansion of previous studies of rock chromaticism. This article defines common types of chromatic progressions occurring in recent art rock, and it identifies harmonic schemas that many post-millennial art-rock songs use to introduce and incorporate chromaticism. The schemas are classified both by the functions of chromatic chords, and the ways in which chromatic progressions are introduced. Chromaticism in art rock, as in classical music, has strong potential for evoking unusual states or creating expressive intensity. Accordingly, the analytical examples in this article also demonstrate that chromaticism conspires with lyrics, vocal performance, timbre, and instrumental texture in order to suggest otherworldliness, ambiguity, or disjuncture.
1. Two Examples of Chromatic Progressions
[1.1] “Offspring Are Blank” is the first track from Dirty Projectors’ 2012 album Swing Lo Magellan. The chorus of the song has musical features that one would expect of an opening track aiming to grab listeners’ attention: loud drums, shouted vocals, and grungy, low distorted guitars. But the introduction and verse play against the chorus’s type; they create an eerie atmosphere through references to exotic folk styles, a melodic line that uses wide leaps and intricate rhythms, a sparse texture, and cryptic, paradoxical lyrics. In keeping with indie styles’ use of timbre to show differentiation from the mainstream, the texture is deliberately sparse instead of full (Blake 2012, [8.4]). In addition, the chromaticism in the opening sections reinforces the sense of otherworldliness and eeriness.
Figure 1a. Dirty Projectors, “Offspring Are Blank” (2012), introduction
(click to enlarge and listen)
[1.2] The song’s introduction, shown in Figure 1a, uses a melodic line drawn from a
Figure 1b. Dirty Projectors, “Offspring Are Blank,” verse 1 (drums not shown)
(click to enlarge and listen)
[1.3] Locke observes that musical exoticism allows a composer to “distort the stylistic norms of his or her musical tradition (until they sound ‘different’) or
[1.4] The first six measures of the verse divide into opening and closing phrases (Moore 2012, 85). Measures 1–2 comprise the opening phrase: in each measure the harmonies move from a tonic to a non-tonic chord. Measures 3–6 comprise the closing phrase: m. 3 moves from a non-tonic to a tonic chord, and mm. 4–6 do the same but double the duration of the harmonies. These measures (4–6) contain the recurring diatonic progression
[1.5] The opening phrase substitutes two different chords that contain
Figure 1c. My Bloody Valentine, “Is This and Yes” (2013), opening
(click to enlarge and listen)
[1.6] In “Offspring Are Blank,” several smooth chromatic progressions provide colorful substitutes for a Phrygian progression. By contrast, the opening of My Bloody Valentine’s “Is This and Yes” (2013), shown in Figure 1c, uses only a single chromatic progression. The track contains long chords played with an organ-like synthesizer sounding over repeated pedal notes played on timpani. The chords are almost entirely from the “white-key” diatonic collection, and vaguely suggest C as tonic. The first two chords use the contrary-motion voice leading
2. Mapping Chromatic Progressions Involving Seventh Chords
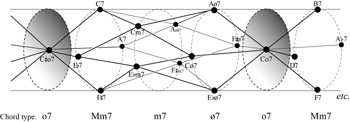
Figure 2a. Tube-shaped voice-leading map for seventh chords
(click to enlarge)
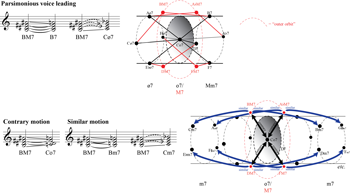
[2.1] Because the parsimonious, contrary-motion, and similar-motion progressions are used frequently in art rock, it is valuable to identify all of their possible iterations in order to determine the range of options a song is selecting from. Figure 2a performs this task for parsimonious progressions by mapping four types of seventh chord onto a three-dimensional tube.(17) Each circular cross section, outlined with a dotted line, contains chords of the same type, and two chords connected by a line segment are parsimoniously related.(18) At the leftmost end of the map is
Figure 2b. An extension of the tube-shaped seventh-chord map that includes all twelve transpositions of each chord
(click to enlarge)
[2.2] The map in Figure 2a can be extended to include every transposition of a seventh chord; this complete version is shown in Figure 2b. In equal temperament, the tube in Figure 2b is an orbifold: to properly represent it, we would twist the right end a quarter turn clockwise and glue it to the left end.(20) The voice-leading paths form a set of relations, but they cannot form a mathematical function.(21) In this respect, they are unlike other models used to describe voice leading among seventh chords (such as those presented in Bass 2001 and Childs 1998) and do not meet the requirements for forming a generalized interval system.(22) Instead, Figure 2b can be viewed as a cross section of a larger four-dimensional voice-leading space that connects all four-voice chords. The map forms a discrete voice-leading lattice (Tymoczko 2011b, 412–17): one can determine the voice-leading work between any two chords—that is, the total number of semitones that all voices move—by counting the number of segments that it takes to move from one to the other. Voice-leading work provides a useful indicator of how smooth a progression is; it is inversely proportional to how closely related the chords sound (i.e., a low value for voice-leading work indicates a high degree of relation, and vice versa).(23)
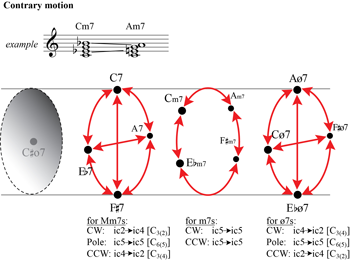
Figure 2c. Notated example of a contrary-motion relation, and contrary-motion relations on the voice-leading map
(click to enlarge)
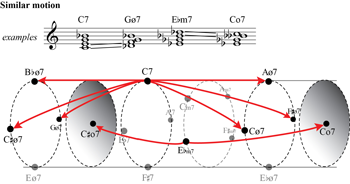
Figure 2d. Notated examples of similar-motion relations, and similar-motion relations on the voice-leading map
(click to enlarge)
Figure 2e. Cross-type progressions
(click to enlarge)
[2.3] Figures 2c and 2d show the possible contrary- and similar-motion progressions, respectively, among the chords on the tube-shaped map.(24) These two progressions are created by the combination of two parsimonious motions, but they could also be conceived of as a single pathway involving the displacement of two semitones.(25) A contrary-motion progression (Figure 2c) occurs within a cross section and is represented by an arrow moving a quarter-turn clockwise or counterclockwise, or, if major-minor 7ths or half-diminished 7ths are involved, across a pole.(26) For major-minor 7ths and half-diminished 7ths, each arrow direction indicates contrary motion of a specific interval class and thus corresponds to a Cx(y) transformation as defined by Childs (1998, 185–187). Contrary motion between two minor 7ths, by contrast, always involves a motion between two ic5s. In a similar-motion progression (Figure 2d), two voices move in the same direction to lead to a different chord type. Similar-motion relations connect major-minor 7ths with half-diminished 7ths (e.g., C7→Gø7) or minor 7ths with diminished 7ths (e.g., Cm7→Co7). A major-minor 7th or half-diminished 7th chord can use similar motion to move to any chord that is two sections to the right or left on the voice-leading map, except for the chord that is on the opposite pole of the cross section.(27)
[2.4] Finally, some songs use cross-type progressions, which change a seventh chord into a triad or vice versa. Some cross-type progressions exploit seventh chords’ ability to effect minor-3rd root movement with efficient voice leading; as a result, they are easily modeled with seventh-chord chromatic progressions.(28) An example appears on the upper staff in Figure 2e, which shows a major triad moving to a major-minor 7th whose root is a minor 3rd lower. Two analyses are shown to the right of the progression; each models the voice leading of the progression using the inclusion and exclusion operations, which transform a major triad into the unique major-minor 7th that contains it and vice versa (Hook 2002, 117–18; 2007, 4–5).(29) The first analysis reduces the second chord to a major triad and models the progression as a combination of R and P (i.e., a relative transformation followed by a parallel transformation). The F, which, as a common tone, provides smoothness, disappears from the progression and only reappears as part of an inclusion operation. By contrast, the second analysis treats the first chord as an incomplete major-minor 7th, which moves to the second through a contrary-motion progression that requires less voice-leading work.(30) Tymoczko (2011b, 100) argues for the same interpretation of this progression, citing the F–D7 progression in Nirvana’s “Heart-Shaped Box” (1993) as an example. A different inclusion relation (marked with a prime
3. Harmonic Schemas for Introducing Chromatic Progressions in Post-Millennial Rock
Table 1. Examples of post-millennial rock songs that use chromatic progressions
(click to enlarge)
[3.0.1] Post-millennial rock songs sometimes introduce chromatic progressions that cannot be easily explained as part of a rock harmonic idiom. These chromatic progressions are often introduced through one of three strategies: (1) in a recurring RN (Roman-numeral) progression, a recurring diatonic progression that can be expressed in Roman numerals is altered to become a chromatic one; (2) in a magic chord, a recurring chord becomes a pivot between normative and non-normative progressions; and (3) in a magic voice leading, a specific voice leading first appears as part of a stylistically normative progression and then reappears, using different chords, in a non-normative progression. Table 1 lists each method of introduction in its column labels. Each column lists some post-millennial rock songs that use each strategy.
[3.0.2] In addition to being categorized by their method of introduction, chromatic progressions can be categorized by one of two functions that they often fulfill: (1) a shuttle or (2) a substitution. Tagg (2009, 173) defines a shuttle as an alternation between two chords that takes place within what he calls “present time”—that is, the span of short-term memory. Generally, both chords have a similar duration and alternate at least twice.(31) Often, a shuttle takes up an entire formal unit. A shuttle does not evince the same tension between tonic and non-tonic chords that is found in longer progressions; instead it forms, in Tagg’s words, a “place to be” (2009, 171)—that is, a static harmonic backdrop. Some shuttles do not imply a specific key. In these cases they are not so much tonally ambiguous as tonally underdetermined—that is, there is not enough information in the melody and harmony to tilt a listener toward hearing a specific tonic. Tagg cites the verse of the Human League’s “Don’t You Want Me” (1981) as a non-key-defined shuttle (2009, 192). The section alternates between F-major and G-major triads, which could be reasonably heard as IV–V in C major,
[3.0.3] In a substitution, a passage is heard as a transformation of a precedent, through one chord or progression replacing another that it resembles. The transformed precedent can be intratextual (a passage from elsewhere in the song), intertextual (a passage from a different song), or virtual (an implied stylistic norm).(32) Multiple precedents can also pertain to a single passage. Hearing a transformation requires identifying similar features between passage and precedent; as Doll discusses, these features might include the pitch-class content of chords, formal layout and location, melody, and timbre (2009, 27–30).
[3.0.4] The voice-leading map shown in Figure 2b provides one means of ascertaining similarity, because chords that are close on the map will likely have more common tones and move to the next chord with nearly the same voice leading.(33) For example, the tritone substitution, where V7 is replaced with “
[3.0.5] Table 1 lists these two common functions for chromatic progressions in its row labels. Each row lists songs that use the type of progression identified in the label: the first row lists songs that use chromatic shuttles, and the second row lists songs that use chromatic substitutions. The following sections discuss each example in greater detail.
3.1 Chromatic Progressions Resulting from Transformation of a Recurring RN Progression
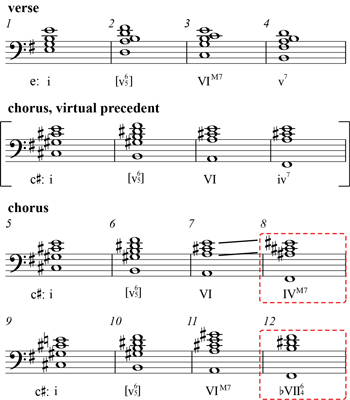
Figure 3.1a. Deerhunter, “Earthquake” (2010)
(click to enlarge)
[3.1.1] Some art-rock songs feature a recurring diatonic progression (which can be expressed through Roman numerals) that is altered to become a chromatic one. The Dirty Projectors’ “Offspring Are Blank,” discussed at the beginning of this article, provides one example, since this song makes several alterations to a
3.2 Chromatic Progressions Resulting from “Magic Chords”
[3.2.1] Some songs feature chords that are marked for memory through frequent repetition and/or unusual voicing.(36) I call them (with a request for the reader’s indulgence) “magic chords,” as they sometimes provide a fulcrum between diatonic and chromatic progressions.(37) Western art music from the second half of the nineteenth century provides a rich precedent for the magic-chord technique: as Tymoczko (2011a, 259) and Smith (2009, 63–69) show, many pieces from this era systematically explore the chromatic voice-leading possibilities of a small number of characteristic chords.
Figure 3.2a. Mew, “Wheels Over Me” (1997), “magic chord” and neighboring chord that appear in introduction. Pitches sound in the octave written
(click to enlarge and listen)
[3.2.2] In Mew’s “Wheels Over Me” (1997), the magic chord, shown in Figure 3.2a, can be described as
Figure 3.2b. Mew, “Wheels Over Me,” first chorus
(click to enlarge and listen)
[3.2.3] In the first chorus, by contrast, the magic
[3.2.4] Grizzly Bear’s “I Live with You” (2009) uses a D6 as its magic chord. This chord functions as a tonic, and its status as a point of repose is especially appropriate since the backing guitar that plays throughout is tuned to the same chord on open strings: <D A D
Figure 3.2c. Grizzly Bear, “I Live with You” (2009), reduction
(click to enlarge)
[3.2.5] Figure 3.2c shows a reduction of the instrumental parts in the first verse and chorus. Notes interpreted as passing or neighboring are enclosed in parentheses. The labeled arrows below the score of the verse show its harmonic schema. After a brief instrumental introduction that presents the chords from the chorus and then features a brief transitional passage for string quartet, verse 1 begins with a series of departures from and returns to the magic chord. The initial departure and return occurs between D6 and E7. This alternation between two chords whose roots are separated by whole step recalls several other rock songs that shuttle between tonic and supertonic in their verse; because of the progression’s ease of execution on a guitar, it often suggests a relaxed initial state.(40)
[3.2.6] Unlike most examples of tonic–supertonic shuttles, both tonic and supertonic in this instance are major triads, implying a Lydian rather than Ionian harmonic progression. While Lydian progressions are rare in rock, I–II is an appropriate descriptor for the verse, since the long duration of the D6, among other contextual factors, asserts D centricity. To be sure, some rock songs alternate between two major triads separated by whole step and later reinterpret these triads as IV and V. An example is REM’s “Man on the Moon”: the verse alternates between C-major and D-major triads and features a melody that centers on the pitches C and G, creating ambiguity as to whether the chords are IV–V or a Lydian-tinged I–II. The prechorus and chorus of “Man on the Moon” are clearly in G major, encouraging a retrospective interpretation of the verse as a IV–V shuttle. By contrast, interpreting the opening of “I Live With You” as a IV–V progression does not reflect the D centricity of the following sections.
[3.2.7] In spite of the relaxed state suggested by the shuttle, the first verse indicates an underlying tension, since its opening chord is not D6 but rather a dissonant polychord that places an
Figure 3.2d. Grizzly Bear, “I Live with You,” transcription of second statement of chorus (3:51–4:12)
(click to enlarge and listen)
[3.2.8] The chorus, also shown in Figure 3.2c, uses the same general harmonic schema as the verse, as shown by the arrows underneath the score. Like the verse, it begins with two alternations between the magic chord and an upper neighbor, continues with a period of intensification through upward transposition, and concludes with a return to the magic chord. The only difference between the schemas is that in the chorus, only one chord is involved in the upward transposition rather than two. But in spite of its harmonic similarity, the instrumental parts are transformed in mood and character, and a disjuncture becomes evident between the accompaniment and the lead singer’s persona. The accompaniment fulfills what Moore (2012, 191) calls an interventionist role: it creates an environment that goes “further than
[3.2.9] The harmonic progression in the chorus amplifies the chaotic environment created by the accompanimental texture. This section exclusively uses chords of set-class [0357], the same quality as the magic chord, but the first two chords are D6 and
Figure 3.2e. Grizzly Bear, “I Live with You,” hypothetical reharmonizations of chorus
(click to enlarge)
[3.2.10] The chorus, in summary, alters the character of the verse by switching from soft to extremely loud, from sparse to dense, from an initial diatonic progression to an entirely chromatic one, and from alternation between minor 7ths and major-minor 7ths to obsessive use of minor 7ths. To further understand the effect of the minor 7ths used in the chorus, it is helpful to imagine counterfactual reharmonizations of the opening phrase. Figure 3.2e shows three harmonizations of the opening two measures of the chorus. In all of them, the accompaniment alternates between two different minor 7ths, and the second chord is consonant with the vocal’s
Figure 3.2f. Grizzly Bear, “I Live with You,” model of voice leading used in chorus
(click to enlarge)
[3.2.11] The role of harmony and abstract voice leading in the chorus is, admittedly, subtler than the obvious contrast created by the change in volume and texture. Nonetheless, the effect of the harmonies used in the chorus is distinct from those of the other potential harmonizations. The voice-leading map in Figure 3.2f shows that the entire chorus, save for its final chord, uses progressions that are characteristic of the initial one: it connects minor 7ths that do not share a diatonic collection, that connect by ascending motion in idealized voice-leading space,(43) and that involve four units of voice-leading work, the maximal amount of work connecting two minor 7ths.
3.3. Chromatic Progressions Resulting from “Magic Voice Leading”
[3.3.1] Other songs incorporate chromatic progressions by first introducing a voice-leading motion as part of a stylistically normative progression, and then revisiting the same voice leading, using different chords, as part of a non-normative progression. I call the voice-leading motions that engender the unusual progressions (with another for of the reader’s indulgence) “magic voice leadings.” They can be construed either as a direction on the voice-leading map (that is, as a specific motion between interval classes) or as a motion between specific pitch classes.
[3.3.2] In the refrain of Radiohead’s “2+2=5” (2003), the harmonization of a chromatically descending bass line introduces characteristic “magic” voice-leading motions. The song’s terminal climax isolates and combines these voice-leading motions to form a new chromatic shuttle.(44) The chromatic shuttle, as will be demonstrated, brings with it a transformation in affect and texture: the new progression removes the cues for melancholy and eeriness that were characteristic of the opening music, and replaces them with a depiction of anger and high arousal.
Figure 3.3a. Radiohead, “2+2=5” (2003), reduction of verse
(click to enlarge and listen)
[3.3.3] Figure 3.3a shows a reduction of the verse/refrain. The guitar is shown on the lower staff, and the two vocal parts are shown on the upper staff—the lead vocal is in large noteheads, and the backing vocal is in small noteheads. The bassist does not play in the section. In mm. 1–11, the vocals and guitar use narrow melodic motion and feature several vertical dissonances. These elements amplify the melancholy state suggested by the minor key, bare soundscape, and lyrics enjoining retreat from the world.(45) In mm. 3, 7, and 11, where the harmony changes from i to V6, a tonic pedal is sustained in an inner voice of the guitar part, creating a dissonant minor ninth with the leading tone in the bass. A dotted slur in the reduction connects the sustained notes. Over the same passage, the lead vocal outlines the chromatic double-neighbor figure C–
[3.3.4] In mm. 9–18, a chromatically descending line from to appears in the lower voices. Classically-trained listeners might also hear the chromatic descent from to as supporting the earlier cues for melancholy, as it is reminiscent of the “lament bass,” which frequently appears in minor-key pieces that suggest sadness or lament.(46) The chromatic descent begins in the lowest voice and is then transferred to an inner voice: the lines in the figure trace the descent. The descent’s registral displacement arises in part from the guitar’s “drop-D” tuning, which makes playing the low C impossible.(47) On the album track, the guitar skips over
[3.3.5] Beginning in m. 13, the backing vocal sings a chromatically ascending line, connected by solid lines in Figure 3.3a, which counterpoints the guitar’s descent. In mm. 13–16, the vertical minor 9ths and major 7ths that characterized the first part of the verse temporarily disappear, yielding instead pure triads and major-minor 7th chords. The change to relative consonance, combined with the motion to a melodic climax, draw attention to the song’s title refrain, “two and two always makes a five.”
[3.3.6] The two chromatic lines in the bass and backing vocal yield several contrary-motion chromatic progressions, departing from the tonic–dominant polarity in the first half of the verse and reflecting the mathematical impossibility of the refrain. In mm. 13–15 F7 moves, via ic2→ic4 (
Figure 3.3b. Radiohead, “2+2=5,” reduction of terminal climax
(click to enlarge and listen)
[3.3.7] The chromatic voice-leading motions introduced in the verse reappear in the song’s terminal climax. The section represents a transformation in affect in comparison with the verse: what was melancholy swells into a state of high arousal, suggesting grief or anger. The piling on of dissonances and snaky melodic lines characteristic of the verse disappear—instead the chords are presented without added dissonances and the melodic line makes wide leaps. In addition, distortion is added to the guitars, creating slightly indigestible timbres (Blake 2012). Osborn identifies vocal high points, loudness, and the repetition of a short, memorable figure as markers of terminal climaxes in rock music (2013, 27–28). In “2+2=5,” the climactic status of the final section is further underscored through maximal chromatic intensity—that is, through presenting a single voice-leading motion that summarizes the previous chromatic progressions and contains the greatest amount of chromatic half steps. The climax, shown in reduction in Figure 3.3b, shuttles between what could be labeled ![]()
[3.3.8] Grizzly Bear’s “What’s Wrong” (2012) introduces two semitonal voice leadings in its verse—B–
Figure 3.3c. Grizzly Bear, “What’s Wrong” (2012), introduction
(click to enlarge)
Figure 3.3d. Grizzly Bear, “What’s Wrong,” reduction of first half of song
(click to enlarge and listen)
[3.3.9] The introductory riff, shown in Figure 3.3c, presents tonal ambiguities that are explored throughout the song. The riff uses notes from the natural diatonic collection, but has contextual reinforcements that suggest F, E, and A as potential tonal centers (Capuzzo 2009, 160). A synthesizer sustains an F-major triad in the upper register. The guitar’s repeated pattern has E as its lowest note and outlines the 5th B–E, but it also contains the 4th A–E. The following verse and chorus, in reduction in Figure 3.3d, assert each of these pitch centers in turn. The verse alternates between Em7 and F major, representing two of the potential tonal centers asserted in the introductory riff. The chorus interprets the verse’s last chord as
[3.3.10] The verse introduces the song’s two “magic” voice-leading motions: B–
[3.3.11] In the interverse (shown on the third system in Figure 3.3d), the previous tonal ambiguity is briefly put in abeyance through a stable Dm7–Gm7 alternation, suggesting i7–iv7 in D minor. The new progression subtly prepared by the last chord in chorus 2, which is a G-minor triad rather than a
[3.3.12] But the clarity provided in the interverse is short-lived: iv7 transforms into a substitute IVadd6 through an ic5→ic5 contrary-motion progression from Gm7 to Em7. The red arrows on the score in Figure 3.3d show that the progression reverses and fuses the B–
[3.3.13] Tonal ambiguity occurs not only in individual sections, but also in the song’s large-scale harmonic plan. The circled chords above the staff in Figure 3.3d show that the minor 7ths that occur at the beginning of the verse and chorus and within the interverse trace a descending-fifth pattern that uses a contrary-motion progression to loop back to its starting point. The sequential nature of the progression militates against hearing any key as tonic. The sequence is shown below the score on a toroidal version of the seventh-chord map; for ease of reading, the map only shows the three minor-7th rings. In order to accommodate the twisted nature of the torus, each ring is rotated 30 degrees, so that when the torus completes one loop it is rotated a quarter turn.
Figure 3.3e. Precedents for Grizzly Bear’s “What’s Wrong”: sequences of four ascending or descending fifths that are reset with a cross-type progression
(click to enlarge)
[3.3.14] The large-scale sequence used in “What’s Wrong” inflates and transforms similar rock progressions that use a sequential chain of four descending or ascending 5ths and loop back to the starting point with a cross-type progression. Figure 3.3e shows examples. The sequences are bracketed, and the cross-type progressions are highlighted in yellow. “I Know There’s an Answer” uses a cross-type progression to lead from I7 to
4. The “Outer Orbit”: Chromatic Progressions Involving Major Seventh Chords
Figure 4a. Mew, “156” (2003), reduction of verse and chorus
(click to enlarge)
Figure 4b. Chromatic progressions involving major-seventh chords
(click to enlarge)
Figure 4c. Tyler, the Creator, “She” (2011), reduction of entire song, with substituted chord shown on bottom staff
(click to enlarge and listen)
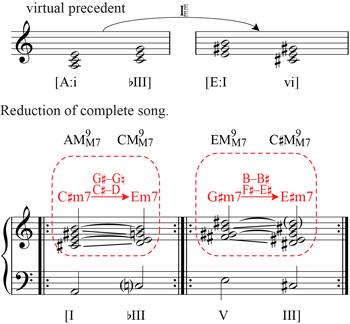
[4.1] The examples studied so far feature chromatic progressions between major-minor 7th and minor 7th chords and occasionally involve o7s and half-diminished 7ths. Some rock songs also introduce major 7ths through the same schemas as those shown in Table 1. For example, Mew’s “156” (2003), shown in Figure 4a, contains a major 7th chord that results from substitution in a recurring RN progression. The verse establishes a norm of an Aeolian descending bass line. The chorus uses the same bass line but descends by 3rd at the end, implying a virtual precedent (enclosed in brackets in the figure). In m. 8, the expected iv7 is replaced with a major IVM7, which results from two chromatic semitones in the upper voices: A–![]()
[4.2] The types of progressions introduced in the first part of this article can also be expanded to include major 7th chords. Figure 4b shows that a major 7th connects parsimoniously to one major-minor 7th by lowering the 7th and to one half-diminished 7th by lowering the root. A major 7th can result from a contrary-motion progression from a diminished 7th: when two voices separated by ic3 contract to form ic1, they form the root and 7th of a major 7th. Unlike major-minor 7ths, half-diminished 7ths, and minor 7ths, contrary-motion progressions using major 7ths do not preserve chord type.(55) Finally, a major 7th connects to two minor 7ths through similar-motion progressions. The maps to the right of the progressions show all possible iterations of parsimonious, contrary-motion, and similar-motion progressions. The major 7ths are in the same cross-section as a diminished 7th, but lie in an “outer orbit” that is further removed from the other chords.
[4.3] The alternative hip-hop song “She” (2011), written by Tyler, the Creator, with a refrain sung by Frank Ocean, uses a major 7th tonic substitute that has similar chromatic relations with both the virtual precedent and the actual chords that precede and follow it. The progression used throughout the song (shown in Figure 4c) suggests a diatonic descent through parallel triads: IV–iii–ii–I.(56) But in a move reminiscent of what Bass calls “chromatic displacement,” in which a song shifts to a diatonic background that is a semitone above or below the original level (1988, 199–201), the last chord is a semitone below the tonic. The arrows on Figure 4c show that the keyboard instrument leads to and departs from the displaced tonic by a progression that involves four units of voice-leading work and no common tones with the original chord (that is, every voice moves by semitone). In addition, the displaced tonic is separated from the hypothetical original by the same relation. The smooth voice leading allows Tyler to both evoke a stock progression and alter it with a minimum of effort, creating an uncanny progression that is both familiar and strange: it is close (in terms of voice leading) to the original, but the diatonic collection from which it hails is far. The progression provides a fitting analogue to the depraved persona the artist adopts in the song: the lyrics juxtapose lines that suggest, as in a traditional love song, that the persona cares for a woman and wishes to have a long-term relationship (“I’m a down to earth nigga with intentions that’s right”), with lines that suggest that the persona intends violence toward a woman (“You’ll be down in the earth if you diss me tonight”) or engages in deviant behavior such as voyeurism and necrophilia.
5. Conclusion
[5.1] In his discussion of chromatic triadic progressions nineteenth-century music, Cohn proposes a model of “hybrid” chordal syntax, in which a listener’s attention shifts between common-practice harmonic functions and parsimonious voice-leading relationships (2012, 195–203). The previous discussions suggest a similar dual syntax in rock music—the songs discussed shift smoothly between diatonic and chromatic and between normative and exceptional progressions. But unlike classical examples, the chromatic progressions in this article grow out of common rock harmonic schemas, such as shuttles, chains of fifth-related chords, diatonic modal progressions, and the use of chord substitution. The unique set of harmonic practices in rock has much to reveal about the potential of chromatic progressions. In particular, art rock’s frequent use of chromatic progressions involving minor 7th chords, as well as its transformation of modal progressions, distinguish it from classical practice.
[5.2] Further study might be undertaken with cross-type progressions that are not easily modeled through inclusion/exclusion operations. For example, Radiohead’s “Knives Out” (2001) concludes each formal unit with an identical ![]()
[5.3] Post-millennial art rock frequently seeks unusual musical personae and rarefied expressive states in comparison to earlier rock styles. It expresses its love in abstruse terms (“Offspring Are Blank”), it rejects a celebration of youth and rebellion in favor of a search for death or retreat (“Wheels over Me” and “2+2=5”), and it eschews a straightforward love song in favor of one that juxtaposes lines about love with those about violence (“She”) or expresses unnatural calm in the midst of a failing relationship (“I Live with You”). While vocal delivery, timbre, and texture are crucial in creating these personae and expressive states, chromatic harmony also plays a significant role. The progressions analyzed in this article create an otherworldly atmosphere or convey a peak of emotional intensity, often supplying the environment that art-rock’s cryptic lyrics only hints at. Given the right tools and stylistic knowledge, we can render explicable these progressions’ potential origins, voice-leading potential, and dramatic effect.
David J. Heetderks
Oberlin Conservatory
Department of Music Theory
77 West College Street
Oberlin, OH 44074
dheetder@oberlin.edu
Works Cited
http://drownedinsound.com/in_depth/4136979-disection--grizzly-bear-veckatimest-track-by-track
Adams, Sean. 2009. “Di-section: Grizzly Bear Veckatimest track-by-track.” Drowned in Sound.
http://drownedinsound.com/in_depth/4136979-disection--grizzly-bear-veckatimest-track-by-track
Bass, Richard. 1988. “Prokofiev’s Technique of Chromatic Displacement.” Music Analysis 7, no. 2: 197–214.
—————. 2001. “Half-diminished Functions and Transformations in Late Romantic Music.” Music Theory Spectrum 23, no. 1: 41–60.
Biamonte, Nicole. 2010. “Triadic Modal and Pentatonic Patterns in Rock Music.” Music Theory Spectrum 32, no. 2: 95–110.
Blake, David. 2012. “Timbre as Differentiation in Indie Music.” Music Theory Online 18, no. 2.
Boilen, Bob. 2012. “How Doo-Wop Unlocks The New Album By Dirty Projectors.” All Songs Considered on NPR Music (July 10). http://www.npr.org/blogs/allsongs/2012/07/10/156534499/how-doo-wop-unlocks-the-new-album-by-dirty-projectors
Boretz, Benjamin. 1972. “Meta-Variations, Part IV: Analytic Fallout (I).” Perspectives of New Music 11, no. 1: 146–223.
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science, New Series 320, no. 5874 (April 18): 346–348.
Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26, no. 2: 177–199.
—————. 2009. “Sectional Tonality and Sectional Centricity in Rock Music.” Music Theory Spectrum 31, no. 1: 157–74.
Causey, Robert. 1994. Logic, Sets, and Recursion. Jones and Bartlett.
Childs, Adrian. 1998. “Moving Beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42, no. 2: 181–93.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1: 9–40.
—————. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. Oxford University Press.
Doll, Christopher. 2009. “Transformation in Rock Harmony: An Explanatory Strategy.” Gamut 2, no. 1: 1–44.
—————. 2011. “Rockin’ Out: Expressive Modulation in Verse-Chorus Form.” Music Theory Online 17, no. 3.
Douthett, Jack and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2: 241–63.
Droste, Edward and Rick Moody. 2010. “Edward Droste.” BOMB 112 (Summer): 68–73.
Empire, Kitty. 2012. “It’ll Take a Good Pitchfork to Penetrate this Grizzly’s Hide
Endrinal, Christopher. 2011. “Burning Bridges: Defining the Interverse in the Music of U2.” Music Theory Online 17, no. 3.
Everett, Walter. 1997. “Swallowed by a Song: Paul Simon’s Crisis of Chromaticism.” In Understanding Rock: Essays in Musical Analysis, ed. John Covach and Graeme M. Boone, 113–54. Oxford University Press.
—————. 2004. “Making Sense of Rock’s Tonal Systems.” Music Theory Online 10, no. 4.
—————. 2008. “Pitch Down the Middle.” In Expression in Pop–Rock Music: Critical and Analytical Essays, 2nd edition, ed. Walter Everett, 111–174. Routledge.
—————. 2009. The Foundations of Rock: From Blue Suede Shoes to Suite: Judy Blue Eyes. Oxford University Press.
—————. 2012. “The Representation of Meaning in Post-Millennial Rock.” Beiträge zur Popularmusikforschung 38: 149–69.
Farber, Jim. 2012. “Hailing Brooklyn’s Heroes of Harmony.” New York Daily News (September 11): 48.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music. University of Chicago Press.
—————. 1997. “After Sundown: The Beach Boys’ Experimental Music.” In Understanding Rock: Essays in Musical Analysis, ed. John Covach and Graeme M. Boone, 33–58. Oxford University Press.
Hawthorne, Marc. 2009. “Jonas Bjerre of Mew.” The A.V. Club (August 26).
Holm-Hudson, Kevin. 2008. Genesis and “The Lamb Lies Down on Broadway.” Ashgate.
—————. 2010. “A Study of Maximally Smooth Voice Leading in the Mid-1970s Music of Genesis.” In Sounding Out Pop: Analytical Essays in Popular Music, ed. Mark Spicer and John Covach, 99–123. University of Michigan Press.
Hook, Julian. 2002. “Uniform Triadic Transformations.” Journal of Music Theory 46, no. 1/2: 57–126.
—————. 2007. “Cross-Type Transformations and the Path-Consistency Condition.” Music Theory Spectrum 29, no. 1: 1–40.
Huron, David. 2008. “A Comparison of Average Pitch Height and Interval Size in Major- and Minor-key Themes: Evidence Consistent with Affect-related Pitch Prosody.” Empirical Musicology Review 3, no. 2: 59–63.
Huron, David, and Turner, Ben. 2008. “A Comparison of Dynamics in Major- and Minor-key Works.” Empirical Musicology Review 3, no. 2: 64–68.
Jackson, Bruce, collector and editor. 1972. Wake Up Dead Man. Harvard University Press.
Kochavi, Jonathan. 2002. “Contextually Defined Musical Transformations.” PhD dissertation, SUNY Buffalo.
Krebs, Harald. 1996. “Some Early Examples of Tonal Pairing: Schubert's ‘Meeres Stille’ and ‘Der Wanderer.’” In The Second Practice of Nineteenth-century Tonality, edited by William Kinderman and Harald Krebs. University of Nebraska Press. 17–33.
Krumhansl, Carol L. 1998. “Perceived Triad Distance: Evidence Supporting the Psychological Reality of Neo-Riemannian Transformations.” Journal of Music Theory 42, no. 2: 265–81.
Lewin, David. 1973–4. “Toward the Analysis of a Schoenberg Song (Op. 15, No. XI).” Perspectives of New Music 12, no. 1/2 (Autumn): 43–86.
—————. 1998. “Some Ideas about Voice-Leading between PCSets.” Journal of Music Theory 42, no. 1 (Spring): 15–72.
—————. 2007. Generalized Musical Intervals and Transformations. Orig. pub. 1993. Oxford University Press.
Lewis, Christopher. 1984. Tonal Coherence in Mahler’s Ninth Symphony. UMI Research Press.
Locke, Ralph P. 2007. “A Broader View of Musical Exoticism.” The Journal of Musicology 24, no. 4: 477–521.
McDonald, Chris. 2000. “Exploring Modal Subversions in Alternative Music.” Popular Music 19, no. 3: 355–63.
Moore, Allan. 2012. Song Means: Analysing and Interpreting Recorded Popular Song. Ashgate.
Nobile, Drew. 2011. “Form and Voice Leading in Early Beatles Songs.” Music Theory Online 17, no. 3.
Osborn, Brad. 2010. “Beyond Verse and Chorus: Experimental Formal Structures in Post-Millennial Rock Music.” PhD dissertation, University of Washington.
—————. 2013. “Subverting the Verse–Chorus Paradigm: Terminally Climactic Forms in Recent Rock Music.” Music Theory Spectrum 35, no. 1: 23–47.
http://www.rollingstone.com/music/news/q-a-dirty-projectors-david-longstreth-lashes-out-at-critics-20120611
Perpetua, Matthew. 2012. “Q&A: Dirty Projectors’ David Longstreth Lashes Out at Critics.” Rolling Stone (June 29).
http://www.rollingstone.com/music/news/q-a-dirty-projectors-david-longstreth-lashes-out-at-critics-20120611
Reale, Haley Beverburg. 2014. “Making the Most of an Enharmonic Seam: Pitch Respellings, Semitone Relationships, and Mode Mixture in Fiona Apple’s ‘Extraordinary Machine.’” Forthcoming in Theory and Practice.
Rockwell, Joti. 2009. “Birdcage Flights: A Perspective on Inter-Cardinality Voice Leading.” Music Theory Online 15, no. 5.
Russell, Amy. 2013. “Dirty Projectors’ Seventh Studio Album Is Their Most Accessible to Date, but That Doesn’t Mean There Isn’t Room for a Little Chaos.” South China Morning Post (January 20): 4.
Santa, Matthew. 1999. “Defining Modular Transformations.” Music Theory Spectrum 21, no. 2 (Autumn): 200–229.
Satyendra, Ramon. 2004. “An Informal Introduction to Some Formal Concepts from Lewin’s Transformational Theory.” Journal of Music Theory 48, no. 1: 99–141.
Sisario, Ben. 2007. “Pop.” The New York Times (August 31): 18.
Smith, Charles J. 1986. “The Functional Extravagance of Chromatic Chords.” Music Theory Spectrum 8: 94–139.
Smith, Peter H. 2009. “Brahms’s Motivic Harmonies and Contemporary Tonal Theory: Three Case Studies from the Chamber Music.” Music Analysis 28, no. 1: 63–110.
Stephenson, Ken. 2002. What to Listen for in Rock: A Stylistic Analysis. Yale University Press.
http://pitchfork.com/features/interviews/8883-dirty-projectors/2/
Stosuy, Brandon. 2012. “Interview with David Longstreth.” Pitchfork (July 2).
http://pitchfork.com/features/interviews/8883-dirty-projectors/2/
Straus, Joseph. 1982. “Stravinsky’s ‘Tonal Axis.’” Journal of Music Theory 26, no. 2: 261–90.
Tagg, Philip. 2009. Everyday Tonality. The Mass Media Music Scholars’ Press.
Tiemann, Laura and Huron, David. 2011. “Beyond Happiness and Sadness: Affective Associations of Lyrics with Modality and Dynamics.” Empirical Musicology Review 6, No. 3: 147–54.
Tymoczko, Dmitri. 2005. “Voice Leadings as Generalized Key Signatures.” Music Theory Online 11, no. 4 (October).
—————. 2006. “A Geometry of Musical Chords.” Science 313, No. 5783 (July): 72–74.
—————. 2009. “Three Conceptions of Musical Distance.” Bridges 2009: Mathematics, Music, Art, Architecture, Culture. Proceedings of Bridges Banff 2009. Banff, Canada: Tarquin Books. 29–38.
—————. 2011a. “Dualism and the Beholder’s Eye: Inversional Symmetry in Chromatic Tonal Music.” In The Oxford Handbook of Neo-Riemannian Music Theories, ed. Edward Gollin and Alexander Rehding, 246–67. Oxford University Press.
—————. 2011b. A Geometry of Music. Oxford University Press.
Weingarten, Christopher R. 2012. “Head Spin: Location, Location, Location.” Spin 28 (September): 94.
Weiss, Robert M. 1999. “Das Kontinuum.” In Josef Matthias Hauer: 80 Jahre Zwölftonmusik, ed. Robert M. Weiss, 30–31. Universal Edition.
Yeary, Mark. 2013. “Stravinsky’s Passport: The Design and Use of Memorable Chords.” Presentation at Music Theory Midwest Annual Conference, Norman, OK, April 26.
http://pitchfork.com/reviews/albums/17037-shields/
Zoladz, Lindsay. 2012. “Review of Grizzly Bear, Shields.” Pitchfork (September 17).
http://pitchfork.com/reviews/albums/17037-shields/
Footnotes
1. The labels “art pop,” “experimental pop,” “art rock,” and “experimental rock” in popular criticism of post-millennial bands occur so frequently that it would be impractical to identify every instance. Empire (2012) coins the term “Pitchfork Pop” to describe Animal Collective, Grizzly Bear, and Dirty Projectors, bands who are also frequently labeled “art rock,” saying that the genre was “a questing, mature vein of post-collegiate music that owed something to folk and found itself on nodding terms with the avant garde but sold plenty of copies too” (33). In Spin, Weingarten (2012, 94) labels Grizzly Bear, Dirty Projectors, and Animal Collective as “Brooklyn art rock,” and he notes that they predicted and influenced elements from more recent pop music. A Rolling Stone interview by Matthew Perpetua (2012) with David Longstreth groups Dirty Projectors with Grizzly Bear and St. Vincent.
Return to text
2. The term “chamber pop” appears in Zoladz (2012) and often implies the inclusion of orchestral and acoustic instruments. Robert Christgau provides one notable dissent from the critical consensus on the label for the band’s style, asserting that because of their emphasis on atmosphere—and what he views as their lack of melody and hooks—their music is better described by the term “folk-prog,” a term he uses somewhat pejoratively (see http://www.robertchristgau.com/get_artist.php?name=Grizzly+Bear). Tame Impala is unique among the post-2000 artists mentioned in this article in that they are most frequently labeled “psychedelic rock” rather than “art rock”; their generous use of reverb and frequent use of flanging effects clearly align them with earlier psychedelia. On flanging effects, see Moore (2012, 47).
Return to text
3. For examples, see Empire (2012), Farber (2012), Russell (2013), Sisario (2007), and others.
Return to text
4. Many of the bands discussed in this article were in fact influenced by 1990s indie-rock bands: Edward Droste of Grizzly Bear cites Pavement and Liz Phair as early influences (Droste and Moody 2010, 69–70), and Jonas Bjerre of Mew cites My Bloody Valentine, The Pixies, and Dinosaur Jr. (Hawthorne 2009).
Return to text
5. The exceptions are Tyler, the Creator’s album Goblin, which was praised but received a score of 8.0 for being too long; and Mew’s albums, which were not reviewed. As a point of comparison, the average Pitchfork rating as of 2007 was 6.3. Nearly every Pitchfork review of the albums discussed in this article makes reference to the bands’ independence from the mainstream and their use of intricate textures. The artists considered here tend to have a polarizing effect on listeners, and the characteristics that attract praise from Pitchfork also attract scorn from those who interpret the concern with craft and stylistic independence as preciosity. Such scorn is evident in Robert Christgau’s lukewarm reviews and an Amazon.com reviewer who dismissed a Dirty Projectors album with the words “hipster Crap—tight pants must be blocking off bloodflow to the brain” (L. Netters’ review at http://www.amazon.com/gp/pdp/profile/A3ECA1PYVR3K1C/ref=cm_cr_pr_pdp). Boilen (2012) has also discussed the polarizing effect of Dirty Projectors.
Return to text
6. Everett (1997 and 2009) relies on Schenkerian voice-leading paradigms to explain chromatic notes. Harrison (1997) uses theories of chromatic harmonic function in his discussion of the music of the Beach Boys. McDonald (2000) identifies chromaticism in 1990s alternative rock as a result of modal “subversion”—that is, introducing and then contradicting a mode through mixture or more advanced chromatic minor-third relations. Reale (2014) examines voice leading and the harmonization of chromatic notes to uncover enharmonic paradoxes in Fiona Apple.
Return to text
7. Capuzzo (2004), Holm-Hudson (2010), and Kochavi (2002).
Return to text
8. The Phrygian with raised is often called the Phrygian major or Phrygian dominant scale. Both forms of the Phrygian scale (with lowered and raised ) appear occasionally in rock music. Examples include Dick Dale’s cover of the folk tunes “Misirlou” (1962) and “Hava Nagila” (1963), the guitar solo in Agent Orange’s “Bloodstains” (1979), and the guitar riff used in The Offspring’s “Come Out and Play (Keep ’Em Separated)” (1994). More recently, the noise-rock band Liars has built entire songs on the Phrygian scale with raised , to striking harmonic effect, in “Houseclouds” (2008) and “Octagon” (2012); the latter song uses both raised and lowered . Everett (2009, 253–55) identifies several other songs that contain
Return to text
9. Compare the opening of “Offspring are Blank” with the songs on Negro Prison Songs from The Mississippi State Penitentiary; A Selection, Historical Recordings From Parchman Farm 1947, recorded by Dr. Harry Oster, available at http://archive.org/details/negroprisonsongs, or Prison Songs: Historical Recordings from Parchman Farm 1947–1948, Volume One: Murderous Home, from the Alan Lomax Collection (Rounder CD 1714). Jackson (1972) discusses the genre of prison work songs and also includes recorded interviews with the singers themselves. The work songs that are synchronized with repeated axe- or hoe-strokes are labeled “axe songs” and “flatweeding” songs in his classification scheme.
Return to text
10. Of the 44 notated examples of prison work songs provided in Jackson (1972, 167–303), none use what could be construed as a Phrygian scale. Most songs were transcribed with notes from a pentatonic collection (10 songs) or with a blues-inflected pentatonic collection that includes both a raised and lowered , assuming that the final note is (19 songs). Among the rest of the songs, notation in major (6 songs) or Mixolydian (4 songs) is most common. To be sure, these observations by no means constitute a normative description of the work song’s stylistic features, because these songs were primarily recorded from only three prisons in Texas in 1964 (Jackson 1972, xix) and because they are mediated through the transcriber’s notation. Nonetheless, they do demonstrate that representative songs do not match the pitch organization of “Offspring Are Blank.”
Return to text
11. This voice-leading reduction assumes “symmetry” (i.e., equivalence) of octave transfer, permutation, and cardinality change (i.e., doubling); see Callender, Quinn, and Tymoczko 2008, 346–347 and Tymoczko 2011b, 25–61. Cohn calls this voice leading “idealized” (2012, 6) and attributes the term to Godfrey Winham; Lewin calls a similar model of voice leading “maximally close” (1998, 17). Tymoczko defines the voice leading as a metric using the log frequency and imposing octave equivalence, folding a point in Rn onto an orbifold (2009, 29).
Return to text
12. The Roman numerals in this article are shown in relation to the major scale. This is a terminological convenience, not meant to imply that the major scale has a privileged status in rock. Flats and sharps before a Roman numeral represent raising or lowering the root by semitone, regardless of which accidentals would appear in staff notation; thus, in the key of E minor, a G-major triad is
Return to text
13. Voice-leading work is one of several possible metrics that might be used to evaluate the relation between two chords. Different metrics are discussed in Cohn (2012, 5–8) and Tymoczko (2009; 2011b, 75).
Return to text
14. Both the contrary motion and similar motion can involve any two voices in the chord, but they are generally restricted to those that connect specific chord-types. Childs (1998) restricts the progressions to those that connect chords of set-class [0257]. I restrict them to those that connect chords that are listed in Fig. 2d.
Return to text
15. Boretz regions comprise eight chords surrounding a central diminished-7th chord: four half-diminished 7th chords that displace one note upward by semitone, and four major-minor (or dominant) 7th chords that displace one note downward by semitone; see Cohn (2012, 152–55).
Return to text
16. In an interview with Pitchfork (Stosuy 2012), lead singer David Longstreth cites unusual textural juxtapositions in contemporary country songs as an influence on “Offspring Are Blank.”
Return to text
17. The resulting construct is a subset of the Four-Cube trio (Douthett and Steinbach 1998, 256; Cohn 2012, 157–58), a spatial voice-leading graph that connects three four-dimensional cubes by touching their corners. An early precedent for mapping parsimonious connections between 7th chords can be found in the “Kontinuum,” a method of presenting a twelve-tone series developed by composer Josef Matthias Hauer (1883–1959). The members of the series are apportioned into four voices, and a chord cycle is created in which one of the voices presents a note of the row while the other three voices hold constant (Weiss 1999, 30–31). I am grateful to Weiss for introducing me to Hauer’s theories.
Return to text
18. Other chord types can be included in the graph, such as the “French 6th” (i.e., set-class [0268]), but since they do not figure prominently in rock they are not included here. Cohn discusses the French 6th in the context of this model (2012, 157–58). The tube shape of the voice-leading map is derived, with some modifications, from Douthett and Steinbach’s Pipeline graph (1998, 257–58).
Return to text
19. Tymoczko has shown that voice-leading direction (i.e., moving a voice “up” or “down”) can pertain in pitch-class space if pitch classes are conceived of as isomorphic to points on a circle (2005, [3.1]–[3.12]; 2011b, 145–149). Voice-leading direction is relevant for chords when a voice leading is path-specific (each member of chord X maps to a specific member of chord Y) and crossing-free (the voice-leading paths do not intersect), and when the motion is as small as possible.
Return to text
20. For discussion of the orbifold nature of voice-leading space in which octave equivalence is assumed, see Callender, Quinn, and Tymoczko 2008 (347) and Tymoczko 2006 (73–74), 2009 (29), and 2011b (93–97).
Return to text
21. A function is a set of mappings from a set of elements A onto a set of elements B that fulfills the following conditions: (1) existence: for every x that is an element of A, there is a y that is an element of B such that f: <x, y> (that is, every member of A maps to some member of B); (2) uniqueness: if x is an element of A and y and z are elements of B, and if f: <x, y> and f: <x, z> are members of the function, then y=z (that is, x must map by the function f to just one y) (Causey 1994, 155). Since, for example, a diminished 7th uses what I have defined as the same voice-leading motion (of lowering one note by semitone) to lead to four different major-minor 7ths, the uniqueness property does not hold. Functions and relations are discussed in Satyendra (2004, 101–11).
Return to text
22. The group of intervals for a GIS (Generalized Interval System) must form a mathematical group—that is, a bijective function that is both one-to-one and onto (Lewin 2007, 26). Since the pathways do not form a function, they do not qualify for a GIS.
Return to text
23. Pitch-class parsimony and low voice-leading work can be especially pertinent to guitar-based music—where chord changes are sometimes made by sliding the hand up or down the fretboard—or to other disjunct progressions. Krumhansl (1998, 279) has conducted empirical research that supports the notion that non-conservatory-trained musicians are sensitive to both absolute and “abstract” (that is, pc-based) voice-leading distance when judging the relative fit between chords.
Return to text
24. In contrast to Childs (1998, 185), I use the term progression or relation to describe contrary- and similar-motion voice leading, rather than transformation or operation, due to their lack of status as mathematical functions, discussed above. I am grateful to Steven Rings for his suggestions regarding my terminology.
Return to text
25. Contrary-motion relations have been defined for major-minor 7th and half-diminished 7ths in Bass 2001 and Childs 1998. They have been defined in a special case for minor 7ths—specifically, Rockwell (2009, [25]) uses a near-birdcage graph, defined by a graph of two different set-classes of cardinality 4 and 3, to model the voice leading among minor 7th chords and augmented triads through voice-leading operations characterized by one voice ascending by semitone and one voice descending by semitone. He calls it a “near-birdcage” graph because augmented triads fail to meet his criterion of being able to connect to each other via the same voice-leading vector. But to my knowledge, Figure 2c is the first graph showing contrary motion for all three chord types that emphasizes their minimal displacement from a diminished 7th chord.
Return to text
26. Contrary-motion progressions have been identified as central to the music of the prog-rock band Genesis (Holm-Hudson 2008, 61; 2010).
Return to text
27. As in contrary-motion progressions, the direction of motion on the map—whether straight across the surface of the tube or curving clockwise or counterclockwise—corresponds to motion of a specific interval class in the chord. Which interval class is represented depends on whether the arrow crosses over one of the diminished 7ths, so the precise correspondences with Childs’s (1998) similar-motion operations are too complicated to discuss here.
Return to text
28. By using 7th-chord progressions as the primary model for cross-type progressions, my analyses differ from the cross-type progressions discussed by Capuzzo (2009, 189–93).
Return to text
29. Hook (2007, 11–16) explores cross-type transformations between musical spaces that can be construed to share the same interval group G in order to create graphs with properties that are of interest to his analyses.
Return to text
30. An alternate view of intercardinality voice leading can be found in Rockwell’s P-matrices (2009, [7]).
Return to text
31. Tagg (2009, 173) also states that both chords must appear in root position at some point, so that they can be heard as equally stable. I will refrain from imposing this criterion for shuttles involving seventh chords, because the added dissonant seventh gives all chords roughly equal stability, or more precisely, roughly equal instability.
Return to text
32. Doll (2009, 19) asserts that a stylistic norm should be measured statistically, rather than by goodness of fit to preconceived laws of harmonic succession.
Return to text
33. For examples of analyses made with this criterion, see Tymoczko (2011b, 275), Harrison (1994, 106–15), and Smith (1986, 122–27).
Return to text
34. Tritone substitutions are typically associated with jazz styles, but they can also occur in rock. Everett has identified tritone substitutions in Paul Simon’s music from the 1970s (1997, 130), in several 1960s songs (2009, 246 and 254), and in the music of Amy Winehouse (2012, 160–61).
Return to text
35. Chromatic substitutions have been suggested for other chords as well. Tymoczko, for example, interprets the “Till Eugenspiel chord” and “Tristan chord” as tritone substitutions for ![]()
![]()
Return to text
36. Yeary (2013) identifies several compositional devices Stravinsky uses to create memorable chords, devices that are also applicable to the songs studied in this article. They include isolation, repetition, and creating a chord that is minimally novel through voicing or spacing. The use of memorable and unusual chords is a long-standing rock practice, dating at least as far back as the famous opening chord of The Beatles’ “A Hard Day’s Night” and Hendrix’s “Purple Haze” chord.
Return to text
37. I borrow the term “magic chord” from Wayne Petty, who used it in an informal conversation about the Fø7 in Brahms’s Intermezzo op. 76, no. 4, m. 2. It has also been used to describe memorable, structural chords in Schoenberg (Lewin 1973–4, Santa 1999).
Return to text
38. Because “Wheels Over Me” contains two different passages that qualify as choruses, in that both recur with the same lyrics, I have labeled them as the first and second choruses. The song’s unusual form is typical of Mew, and resembles but does not quite match any of the common alterations to verse/chorus form. Further discussion of alternations and additions to verse/chorus forms can be found in Osborn (2010, 73–76) and Endrinal (2011, [25]–[38]).
Return to text
39. I favor the second interpretation in this paragraph, but others are possible—one of which was suggested by an anonymous reviewer. I am grateful to my reviewers for their questions regarding this section.
Return to text
40. Examples of an opening tonic–supertonic shuttle in the verse include the Beatles’ “Don’t Let me Down” (ii–IM7) (1969), Thunderclap Newman’s “Something in the Air” (I–ii7) (1969), Guess Who’s “These Eyes” (ii7–IM7) (1968), and Lily Allen’s “Smile” (ii7–IM7) (2006), which samples the earlier reggae tune “Free Soul” by The Soul Brothers. Carl Douglas’s “Kung Fu Fighting” (1973) opens with a I–ii shuttle, but at the end of the verse the latter chord is interpreted as a pre-dominant and leads to V. One anonymous reviewer pointed out that these types of progressions frequently occur in reggae. Examples include Bob Marley and the Wailers’ “Man to Man” (I[M7]–ii[7]) (1970), “Soul Rebel” (ii–I[M7]) (1970), and “Rainbow Country” (i–ii) (1968–1972). For further discussion and a list of supertonic shuttles, some of which overlaps with this footnote, see Tagg (2009, 176–77).
Return to text
41. The guitars in the prechorus play a slow “boogie” pattern (Moore 2012, 22), outlining only the root, 5th, and added 6th or 7th, but the complete chords can be inferred from the saxophone parts.
Return to text
42. The addition of several distinct instrumental layers that, through their variety of timbres and rhythms, resist being integrated into a unified texture, create what Blake (2012, [6.6]) calls a heterogeneous texture, linking this song to earlier indie rock from the 1990s.
Return to text
43. Connection through ascending voice-leading motion is labeled “upshifting” in other studies, as discussed in Cohn (2012, 131–38). Note 19 explains how the concepts of “up” and “down” apply to idealized voice-leading space.
Return to text
44. The terminal climax as a formal section and function is defined in Osborn (2013).
Return to text
45. The correlation between soft dynamics, narrow melodic range, and sadness for Western-enculturated listeners is discussed in Huron (2008), Huron and Turner (2008), and Huron and Tiemann (2011).
Return to text
46. A chromatically descending bass line from to
Return to text
47. In “drop-D” tuning the guitar strings are D-A-D-G-B-E from low to high—that is, standard guitar tuning except that the lowest string is tuned a whole step lower. It should be remembered that the bass, which could have provided the low C, does not play in the verse section.
Return to text
48. The refrain’s chromatic progressions recall classical compositional practice. The ic2→ic4 major-minor 7th progression occurs when a deceptive cadence is embellished by an applied dominant: V7–![]()
Return to text
49. One listener suggested that this harmony represents an altered cadential six-four. In some respects, this hearing is plausible, since the chord occurs in a position where a cadential six-four would be expected in common-practice syntax, and the two vocal parts and lowest guitar part contain notes of the tonic triad that resolve down by step to members of V. In addition, Nobile (2011, [3.1]) argues that a root-position tonic harmony immediately before a cadential V can function much like an inverted cadential six-four in 1960s rock songs in SRDC form (a sentential pattern of statement–restatement–departure–conclusion), and Everett identifies a similar “root-position cadential six-four” in Bob Dylan’s 1983 song “License to Kill” (2008, 153). But this hearing must be counterbalanced with the observation that the other notes in the guitar part overwhelmingly assert a pre-dominant function.
Return to text
50. Given the anomaly of the G in the chord, it might be better explained through functional analysis as described in Harrison (1994, 49–64).
Return to text
51. The label “interverse” indicates a passage of music that occurs only once in the middle of a song, includes text, and connects statements of repeated verse/chorus material (Endrinal 2011, [28]).
Return to text
52. As in “I Live with You,” the song’s timbres differentiate it from the mainstream, placing it in the tradition of 1990s indie rock. Unlike mainstream rock, the verse of “What’s Wrong” uses a non-full and heterogeneous texture (Blake 2012, [8.4]).
Return to text
53. “I Know There’s an Answer” also conforms to the Pentatonic 1/4 subset tonal system, described by Biamonte (2010, 106–7).
Return to text
54. As with “Wheels Over Me,” “156” defies conventional formal explanations. Using the symbol “Bk” for the breakout section, the sectional layout is V C Bk V Bk C Bk. The verse and chorus have similar music and thus initially seem to both belong to the verse, while the breakout has musical features associated with a chorus. In addition, the breakout appears at the end of each group of formal units, in the normal position of a chorus. But unlike the true chorus, the breakout has different lyrics each time it appears.
Return to text
55. Dirty Projectors’ “Fluorescent Half Dome” (2009) uses this contrary-motion relation diachronically: the prechorus contains Bm–Am–Do7, and the chorus begins with GM7, the contrary-motion resolution of the previous Do7.
Return to text
56. Examples of this progression include the second half of Bob Dylan’s “Like a Rolling Stone” (1965) and the second half of the first phrase of “Lean on Me” (1972).
Return to text
Copyright Statement
Copyright © 2015 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Cara Stroud, Editorial Assistant
Number of visits:
19432