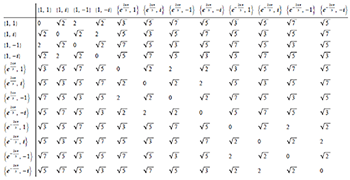Old and New Isometries between Pc sets in the Planet-4D Model
Emmanuel Amiot and Gilles Baroin
KEYWORDS: twelve-tone, pc sets, geometrical model, 4D, isometries, orientation
ABSTRACT: The Planet-4D model introduced by Baroin 2011b is a richer model of pitch-class relationships than the standard cyclic model of the clock-face diagram: instead of the distribution of twelve points on a circle in a 2D plane, the Planet-4D model places the twelve pcs on a 4D hypersphere. Beyond the usual T/I group of symmetries, which is still featured in this new musical space, the additional dimensions yield other isometries (most notably now including the M5/M7 operations), which appear here in animated visualizations of musical pieces. The present article elucidates how these isometries are in fact well-known symmetries that do not preserve shape in most previous models with fewer dimensions. The hyper-spherical environment grants each symbol an equivalent physical position, and therefore allows for more symmetries than any 3D model. This article also shows that the model provides a visually intuitive geometric setting of pcs, in accordance with our perception of 3D Euclidean space, where transpositions by major and minor third are elementary rotations.
Copyright © 2015 Society for Music Theory
1. Brief Sketch of the Model
[1] In the classic 2D circular model of the 12 pcs (the well-known Krenek diagram or clock-face diagram), proximity appears to be restricted to chromatically adjacent points, although other topologies might prove desirable. The Planet-4D model (Baroin 2011b) remedies this restriction by adding two more dimensions to the ambient space, projected here as 3D animations. The 4D model provides a visually intuitive geometric setting of pitch classes, in accordance with our perception of the Euclidean (3D) world, where major- and minor-third transpositions are elementary rotations. The 4D model also allows for all the twelve-tone transformations to be represented as isometries(1)—not only the familiar group of transformations that are generated by transposition and inversion, but also other operations that do not preserve distances under earlier models with fewer dimensions. The aim of this paper is to present the additional symmetries that appear in this model as isometries for Euclidean distance, which is the most intuitive of all.(2) A mathematical description of the model is given in section 1; readers not well versed in mathematics are invited to skip ahead to section 2. Before reading further, however, all readers are invited to look at Video 5 in order to gain a sense of the effectiveness of the model. Section 2 elucidates the elementary motions on the hypersphere, first explaining what is shown in the movies and then moving on to describe the old and new isometries of the Planet-4D model. Twenty-four isometries are identified as the elements of the usual group T/I of transpositions and inversions; twenty-four other isometries are identified with a well-known algebraic group, though one that has never been identified with Euclidean isometries in a music-theoretic setting. In music theory, these additional twenty-four isometries are related by the M5 or M7 operations (multiplication of a pc by 5 or 7, modulo 12), an operation that maps a cycle of fourths or fifths onto the chromatic scale and vice versa. On the 1D circle, the M5/M7 operations do not preserve distance and are thus not isometric, but, surprisingly, in four dimensions they can be represented as isometries. The Appendix collates the proofs of the theorems presented in the main text.
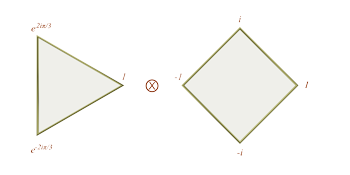
Figure 1. Product \(\mathbf{Z}_3 × \mathbf{Z}_4\) as seen in \(\mathbf{C} × \mathbf{C}\)
(click to enlarge)
[2] In this section we will use the traditional algebraic decomposition of \(\mathbf{Z}_{12}\) as the starting point for an immersion of the 12 pcs in the 4D sphere, in such a way that any pair of pcs separated by a given interval appear at the same mutual Euclidean distance. We begin by labeling every pc in equal temperament as an integer modulo 12. The set of these pitch classes, \(\mathbf{Z}_{12}\), is isomorphic to a group or a graph with the product \(\mathbf{Z}_3 \times \mathbf{Z}_4\), the so-called “torus of thirds” that is familiar in music theory as the equal-tempered Tonnetz—in other words, the modulo 12 group can be represented as the product of a modulo 3 cyclic group and a modulo 4 cyclic group. Explicitly, n modulo 12 is mapped to the pair (n mod 3, n mod 4). Conversely, such a pair of residues \((a,b) \in \mathbf{Z}_3 \times \mathbf{Z}_4\) can be mapped to \(4a - 3b\), which is well-defined modulo 12.(3)
[3] Both sets can then be turned into their complex representations (see Figure 1):
\[
\mathbf{Z}_3 \approx \{1, e^{2i\pi / 3}, e^{-2i\pi / 3}\}
= \{1, -\frac{1}{2} + \frac{i\sqrt{3}}{2}, -\frac{1}{2} - \frac{i\sqrt{3}}{2}\}
\text{ whereas }
\mathbf{Z}_4 \approx \{1, i, -1, -i\}
\]
More precisely, each pair \((a,b) \in \mathbf{Z}_3 \times \mathbf{Z}_4\) is mapped to
\[
(e^{2ai\pi / 3}, e^{bi\pi / 2}) = (\cos(2a\pi / 3) + i\sin(2a\pi / 3), \cos(b\pi / 2) + i\sin(b\pi / 2)).
\]
The twelve pcs thus appear as elements of \(\mathbf{C} \times \mathbf{C}\). For instance,
[4] The ambient space \(\mathbf{C} \times \mathbf{C} =\mathbf{C}^2\) (two complex dimensions) can be seen alternatively as \(\mathbf{R}^4\), a 4D space, since any complex number consists of two real coordinates. Complex coordinates in \(\mathbf{C}^2\) are more convenient for proofs and abstract descriptions, whereas real coordinates in \(\mathbf{R}^4\) are preferred for the computation of movies. Using either system, we can follow through the decomposition of \(\mathbf{Z}_{12}\) into the product \(\mathbf{Z}_3 \times \mathbf{Z}_4\) by projecting onto the two orthogonal planes that sum up to the overall space,
i.e. \(\{(z,0) \in \mathbf{C}^2\}\) or \(\{(x,y,0,0) \in \mathbf{R}^4\}\) and \(\{(0,z') \in \mathbf{C}^2\}\) or \(\{(0,0,x',y') \in \mathbf{R}^4\}\). Using the same example as above, we get for
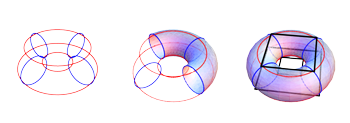
Figure 2. Embedding the torus of thirds in \(\mathbf{R}^3\)
(click to enlarge)
[5] It is more customary to consider the direct product \(\mathbf{Z}_3 \times \mathbf{Z}_4\) as embedded in a product of circles, which is topologically a torus. But when the usual picture of a torus is drawn, distances are distorted. See, for instance, the last image in Figure 2, which represents the product of the circle of minor thirds and the circle of major thirds, shown as a 3D torus in 2D. The diminished sevenths—the black squares inscribed in the red horizontal circle—have different sizes, although their intervals are the all the same size. It can be proved that there is no way to embed \(\mathbf{Z}_3 \times \mathbf{Z}_4\) isometrically in 3D-space, which is one strong vindication of our 4D model.(7) See Video 1 for the construction of a torus in \(\mathbf{R}^3\) (3D space), and Video 2 for the embedding of the product \(\mathbf{Z}_3 \times \mathbf{Z}_4\) in the hypersphere (4D space).(8) In Video 1, minor-third cycles (diminished-seventh chords) are shown as red squares, major-third cycles (augmented triads) as green triangles, and semitonal motion along the torus is shown with blue arrows. Video 2 represents the pcs at the vertices of these 2D squares and triangles as small 3D objects. Objects of the same color are related by minor third, and objects of the same shape are related by major third.
|
Video 1. Construction of a torus in \(\mathbf{R}^3\) (click to watch video) |
Video 2. Embedding of the product \(\mathbf{Z}_3 × \mathbf{Z}_4\) in 4D space (click to watch video) |
2. Moving Around the Hypersphere
2.1 Moving in Movies
[6] In this section we explain how the 4D model is projected onto a screen with minimal distortion, so that its Euclidean geometry can be perceived as accurately as possible. We describe the basic motions: minor thirds appear as rotations in the first two dimensions and major thirds as rotations in the last two. A brief description of the extension of the model from intervals to pc sets (such as triads) is provided, with a visualization of a famous chord progression from the Scherzo of Beethoven’s Ninth Symphony as a video example.
Video 3. Elementary rotations in the planet 4D model
(click to watch video)
[7] The two basic moves in the 4D model are major-third and minor-third transpositions, which are represented as rotations in the two complex dimensions of \(\mathbf{R}^4=\mathbf{C}^2\). In order to create 2D videos, the four coordinates of a pc (or pc set; see below) in our 4D model are first projected orthographically into 3D(9), then drawn as colored 3D objects (spheres, cubes, etc.), and finally visualized on the 2D screen of the computer. This projection induces a small amount of deformation (as in the more familiar perspective projections of a tesseract, or 4D hypercube, into 2D, which distorts the sizes and shapes of the constituent cubes), but the deformation is minimized because the model is user-centered, in contrast to most other models. In Video 3 the hypersphere rotates in front of the user, symbolized by a rotating ball centered on the screen.
[8] Each pc is identified by a unique combination of three colors representing component \(z\) and four shapes representing component \(z'\). If we move by minor thirds, the shape changes but not the color, because component \(z\) is constant and only \(z'\) changes. If we move by major thirds, the color changes but not the shape, because \(z\) changes but \(z'\) does not.
[9] Video 3 shows both of the elementary rotations, representing transpositions upward by minor thirds and by major thirds. These elementary rotations happen in two completely independent subspaces: one transposition rotates the complex component \(z\) while the other rotates \(z'\), with the axis of rotation going through the centers of all triangles or the centers of all squares, respectively.
[10] Video 3 also shows that transposition upward by semitone (up a major third, down a minor third) combines two such rotations, changing both the color and shape of the components.
| \((z;z') \mapsto (z.e^{2i\pi / 3};z')\) | major third transposition |
| \((z;z') \mapsto (z;i z')\) | minor third transposition |
| \((z;z') \mapsto (z.e^{2i\pi / 3};-iz')\) | semitone transposition |
Transpositions by perfect fifth (i.e., up or down one major third plus one minor third) would likewise combine two elementary rotations.
[11] The movies are created by interpolating motions between discrete states, thus providing continuous paths in the spirit of Mazzola’s (2007) gestures, which purport to answer David Lewin’s question, “If I am at s and wish to get to t, what characteristic gesture should I perform in order to arrive there?” (1987, 159).(10)
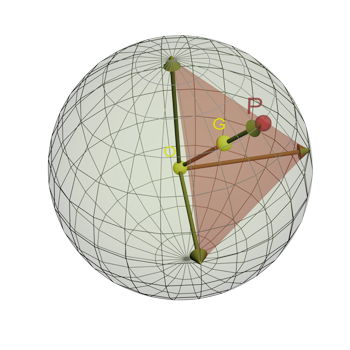
Figure 3. Projection of the barycenter of a trichord on the surface of the sphere
(click to enlarge)
[12] This model of 4D space can be extended from pitches to pc sets by the simple expedient of projecting the center O of the sphere through the barycenter G of all pcs involved on the surface of the sphere into point P; see Figure 3 and Video 4. The picture is shown in 3D for readability, but the principle is the same in any dimension: in this example, a spherical triangle (i.e. a trichord) is summarized by its center.
[13] The famous progression of major and minor triads beginning at m. 143 of the middle section of the Scherzo of Beethoven’s Ninth Symphony, an RL cycle(11) discussed in Cohn 1991 and 2012, can be modeled on the hypersphere using this convention; see Video 5. The center of the screen shows triplets of numbers—which are the pcs involved—and in the centers of the triangles are labels for each triad: C, a, F, d, etc. The smooth, short moves between the triads allow the observer to appreciate the parsimonious voice-leading: each pair of triads holds two tones in common, while one note moves by a single whole or half step.
|
Video 4. Projection of the barycenter of a trichord on the surface of the sphere (animated) (click to watch video) |
Video 5. Rotations in the RL cycle of triads from the Scherzo of Beethoven’s Ninth Symphony (click to watch video) |
2.2 The Usual Isometries
[14] We now look at the effect of the T/I group, which acts as a subgroup of the rotations in 4D space. Transpositions, musically speaking, are simply translations in \(\mathbf{Z}_{12}\) or in the isomorphic \(\mathbf{Z}_3 \times \mathbf{Z}_4\). For instance, the semitone transposition \(T_1\) is \(x \mapsto x+1\) in \(\mathbf{Z}_{12}\) and \((a,b) \mapsto (a+1,b-1)\) in \(\mathbf{Z}_3 \times \mathbf{Z}_4\). In the 4D model, this means rotating both complex components in \(\mathbf{C}^2\), up one major third and down one minor third, or equivalently, rotating the two pairs of real coordinates in \(\mathbf{R}^4\). The matrices of a semitone transposition are respectively
Video 6. T2 transformation
(click to watch video)
Figure 4. Projection of the barycenter of a trichord on the surface of the sphere (animated)
(click to enlarge)
Figure 5. Product of axial symmetries
(click to enlarge)
[15] Geometrically (and visually), a transposition is thus composed of rotations of the two orthogonal planes whose direct sum makes up the space. A decomposition of \(T_2\) as two minor thirds up and one major third down is shown in Video 6; see also Figure 4. The arpeggiated major triads in Video 6 move with parsimonious voice leading up by minor thirds from C to
[16] Inversions are also represented as rotations in \(\mathbf{R}^4\). An inversion in \(\mathbf{Z}_{12}\) is a mapping \(z \mapsto c-z\), which is equivalent via isomorphism to \((x,y) \mapsto (a-x,b-y)\) in \(\mathbf{Z}_3 \times \mathbf{Z}_4\). Each of the components of this map \[ x \mapsto a-x \qquad y \mapsto b-y \] is an axial symmetry in the equilateral triangle and square components, respectively.
[17] The direct product of those two symmetries is an orthogonal symmetry around the plane in \(\mathbf{R}^4\) built up from the two axes (the eigenvalues are \(1,1,-1,-1\)). This isometry has determinant \(+1\); hence it is technically and visually a rotation in \(\mathbf{R}^4\) (with angles 0 and \(\pi\), so that mathematicians call it a half-turn in 4D), as in the video representing the passage from Beethoven’s Ninth Symphony scherzo. Geometrically, it is an orthogonal symmetry around the plane built from one axis of symmetry in the triangle and another one in the square. (The orthogonal symmetry is difficult to draw in 4D but easy to imagine: the plane of fixed points of this symmetry intersects both component planes in two axes, which are axes of symmetry of the triangle \(\mathbf{Z}^3\) and the square \(\mathbf{Z}^4\).) In the T/I group, there are two kinds of inversions, those with two fixed points, where the axis of inversion is two pcs a tritone apart (i.e., inversions with even index numbers), and those with none, where the axis of inversion falls between pairs of adjacent pcs a tritone apart (i.e., inversions with odd index numbers). In this model, the number of fixed points depends on whether the second axis, in the square, passes through vertices or joins midpoints of opposite sides. The two kinds of inversions are shown in Videos 7 and 8 respectively; see also Figure 5. Video 7 shows an I4 transformation with two fixed points: the C-major triad [0,4,7] is inverted onto the A-minor triad [9,0,4], which is equivalent to the operation T4I. Video 8 shows an I3 operation with no fixed points: the C-major triad is inverted onto the B-minor triad [11,2,6], equivalent to the operation T11I.
|
Video 7. I4 transformation (click to watch video) |
Video 8. I3 transformation (click to watch video) |
[18] An interesting feature demonstrated by the Planet-4D representation is the following:
Proposition 1. All transformations of the T/I group are orientation-preserving isometries in \(\mathbf{R}^4\).
Video 9. Inversion as rotation: 014 becomes 034 in Webern’s Bagatelle for String Quartet op. 9, no. 5
(click to watch video)
In other words, in this model, inversions no longer “flip” or reverse shapes, but rotate, like a transposition in a lower-dimensional model. For instance, in Video 9, we see 014 rotated rather than reflected onto 034 (inversion around pc 2) in the opening of Webern’s Bagatelle for String Quartet op. 9, no. 5.
2.3 The New Isometries
[19] During the dissertation defense of Baroin 2011b, it was observed that some isometries in 4D space were not part of the usual T/I group. A member of the jury then directed a master’s student to search for all the isometries of the Planet-4D model; see Baixas 2012. We discovered in consequence that these new isometries are, in fact, well known but even better disguised transformations of pc space. Since they had never before been represented as isometries (save once, cf. Theorem 2), and are not easily recognizable otherwise, we call them “the new isometries.” The result is as follows, with the proof given in the Appendix:
Theorem 1. The Planet-4D model has 48 isometries.
[20] We can build 48 isometries as direct products of the 6 isometries of an equilateral triangle (the dihedral group \(D_3\)) and the 8 isometries of the square (the dihedral group \(D_4\)). The resulting group is twice as large as the T/I group, and is mapped onto \(\mathbf{Z}_{12}\) as the dihedral group \(D_{12}\).
[21] Notice that:
- A product of two rotations is a transposition in \(\mathbf{Z}_{12}\). For instance, rotating one major third up and one minor third down yields a transposition by semitone. There are 12 (\(3 \times 4\)) such transpositions.
- A product of two axial symmetries is an inversion in \(\mathbf{Z}_{12}\). For instance, in \(\mathbf{Z}_3 \times \mathbf{Z}_4\), combining the symmetries \(a \mapsto -a\) and \(b \mapsto -b\) into \((a, b) \mapsto (-a, -b)\) yields inversion around the axis C–
F♯ , turning the C-major triad into an F-minor triad. There are 12 (\(3 \times 4\)) such inversions.
This accounts for the whole of the traditional group T/I and its 24 elements, which are all rotations (i.e. orientation-preserving isometries) in \(\mathbf{R}^4\). The new isometries have the following form:
- A product of a symmetry by a rotation (or, conversely, a rotation by a symmetry) reverses its orientation. For instance, in the transformation \((x,y) \mapsto (x-1\ \mathit{mod}\ 3, 1-y\ \mathit{mod}\ 4)\), the pitches of the C-major triad, C = (0,0), E = (1,0), and
G = (1,3) become F = (2,1), A = (0,1), andF♯ = (0,2) respectively. There are \((3 \times 4) + (3 \times 4)=24\) such isometries.
Here is the 4D matrix of one of the 24 new isometries, which rotates the triangle and flips the square around one diagonal: \( \begin{pmatrix} -\frac{1}{2} & \frac{\sqrt{3}}{2} & 0 &0 \\ -\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 &0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}\).
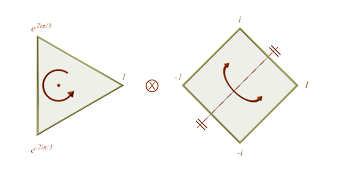
[22] In the discrete torus of thirds \(\mathbf{Z}_3 \times \mathbf{Z}_4\), this is equivalent to \((x,y) \mapsto (x-1\ \mathit{mod}\ 3, 1-y\ \mathit{mod}\ 4)\). An illustration is given in Figure 6.
Figure 6. Rotation times axial symmetry
(click to enlarge)
Video 10. Rotation times axial symmetry
(click to watch video)
Video 11. Beethoven through the looking glass
(click to watch video)
[23] The proof of the theorem given in the Appendix confirms that the list is exhaustive, and thus that all possible isometries of the model pertain to one of the forms enumerated above.
[24] Major or minor triads provide a helpful demonstration of this larger group: the original T/I group acts simply transitively on these 24 triads; in other words, there is exactly one way to transform one given triad into another one by way of a T/I transformation. This is one of the most famous generalized interval systems as defined in Lewin 1987.
[25] Applying any of the new isometries, however, turns these triads into the so-called major-minor trichords, i.e., transpositions of 014 or 034, set class 3-3 in Forte’s classification. (In Fiore, Noll, and Satyendra 2013 these chords are called “jets” and “sharks” respectively, in honor of their use in the score of Bernstein’s West Side Story.) One example of such a transformation was given above in [21.3]. To give another example, the transformation \((x, y) \mapsto (2+x, 3-y)\) turns the pitches of the C-major triad,
[26] Some useful features of the new group are given in Proposition 2. Theorem 2, below, explains why they may look familiar to many readers.
Proposition 2. The product of two new isometries is an old one: an element of the T/I group. More specifically, applying one of the new transforms twice yields a transposition by either a major third or a tritone.(12) The product of a new isometry by any old one is a new one.
This proposition is derived from the characterization of the T/I isometries by the value 1 of their determinant and the new isometries by the value -1 of their determinant. T/I is a normal subgroup (with index 2) in the 48-element group of all isometries of the 4D model.
[27] In order to better grasp the meaning of these new transforms, we applied the new isometries to the diatonic and pentatonic scale, and noticed a striking fact:
The transform of a diatonic or pentatonic scale by any of the new (indirect) isometries is a chromatic collection and vice versa.
Video 12. Pentatonic to chromatic
(click to watch video)
For instance, \((x,y) \mapsto (x-1,3-y)\) turns the pentatonic C–G–D–A–E or (0,0), (1,3), (2,2), (0,1), (1,0) into (2,3), (0,0), (1,1), (2,2), (0,3), the chromatic collection B–C–
[28] This relationship has been observed by Mazzola (2002, 622):
Theorem 2. The isometries of the torus of thirds \(\mathbf{Z}_3 \times \mathbf{Z}_4\) with the “natural” metric are the affine transforms in the isomorphic ring \(\mathbf{Z}_{12}\), e.g. \[ x \mapsto ax + b \in \mathbf{Z}_{12}, \quad a \in \{1, 5, 7, 11\}, \quad b \in \mathbf{Z}_{12} \]
Thus the group of isometries of the Planet-4D model is actually isomorphic with the rather better-known affine group on \(\mathbf{Z}_{12}\), which extends T/I with the multiplicative operators M5 and M7 (see, for instance, Rahn 1980, 53–56). An independent proof of this is given in the Appendix.
[29] There is another little-known result (which we have not found stated elsewhere) that clarifies the relationship between preserving geometric shapes and the affine group:
Theorem 3. Any permutation of Zn that induces a permutation of orbits under T or T/I must be an affine transformation \(x \mapsto a x+b\) (with \(a\) invertible modulo \(n\)).
“Inducing a permutation of orbits” means that if, for instance, the image of one particular minor triad is a shark (014), then the image of any major or minor triad must be either a shark or a jet (034); that is, a given geometrical shape is always mapped to the same (other) shape. This result is actually elementary (the proof is given in the Appendix).
[30] This suggests another derivation of the 48-element group, as a semi-direct product \(K \rtimes \mathbf{Z}_{12}\) of the Klein group with four elements (\(a \text{ in } ax+b\)) by \(\mathbf{Z}_{12}\) acting by translation (\(b \text{ in } ax+b\)), instead of a direct product of two dihedral groups \(D_3 \times D_4\), which is the way we constructed it originally.
[31] Another way to look at this group structure is as an extension of the traditional dihedral group T/I \(\rtimes \) \( \mathbf{Z}_2\) in the sense of Popoff 2013, a group whose action is simply transitive on the union of triads (major or minor) and jets and sharks, wherein the “second dimension” specifies the “shape,” i.e. whether a triad is turned into another triad, or into a jet or shark. Considering the many different non-isomorphic possible extensions of T/I with 48 elements, it is highly significant that the one we studied should be the affine group of \(\mathbf{Z}_{12}\) already well-known in music theory.
2.4 Conclusion
[32] So—is this model worthwhile? We think it is, for the following reasons:
- Mazzola’s (2002) theorem deals with the abstract relationship between \(\mathbf{Z}_{12}\) and \(\mathbf{Z}_3 \times \mathbf{Z}_4\). Here the representation of the modulo 12 cyclic group as the product of modulo 3 and modulo 4 groups is embodied in physical space, made visible and within the grasp of our senses.
- All of the 48-element groups discussed here (\(D_3 \times D_4, \mathit{Aff}_{12}, K \rtimes \mathbf{Z}_{12}, D_{12} \rtimes \mathbf{Z}_2\)) are isomorphic. But this algebraic truth does not deter us from trying to visualize this group in the most intuitive way possible. The first visualization, represented as a group of isometries in Euclidean space, is certainly closest to human intuition; the so-called “natural” metric on a Torus is much harder to visualize.(13)
- Among all possible overgroups of T/I, this group of isometries is naturally isomorphic with another known group, the M5/M7 operations. Thus all the twelve-tone operations can be shown as isometries in this model.
- Last but not least, the Planet-4D model represents inversions and M5/M7 operations as continuous moves, which in earlier models are only possible with transpositions. This new feature of the added dimensionality is obvious in the movies, wherein a move from one pitch class (or chord) to another is not a discontinuous jump but a smooth gesture, as defined in Mazzola and Andreatta 2007.
[33] These isometries were already identified, but only as an abstract conceptual result, which, like sleeping beauties, needed to be awakened in the 4D world for us to appreciate their exquisite charm.
3. Appendix
3.1 Proof of Theorem 1
[34] The new isometries are described in the main text. We prove here that the list is now complete. The proof given here is simpler than that given in Baixas 2012. The 48 isometries described henceforth make up a subgroup of the whole group. We endeavor to prove that this subgroup is equal to the whole.
Figure 7. Distances between pcs on the Planet-4D model
(click to enlarge)
[35] The Planet-4D model is a polytope with 12 vertices that contains three squares and four equilateral triangles, obtained by moving only one component (either \(k\) or \(\ell\)) of the generic point \((e^{2ik\pi / 3}, e^{2i\ell\pi / 4})\) in complex notation. Any isometry of this polytope must map a square onto a square and a triangle onto a triangle. To be completely rigorous, it must be confirmed that there are no other squares (resp. equilateral triangles) than these in the model, and that is readily evident from the mutual distances between vertices; see Figure 7.
[36] Now let us consider an arbitrary isometry preserving the polytope. Say it turns a triangle \(T_1\) into triangle \(T_2\), meaning in complex components that for any \(k, \{(e^{2ik\pi/3},u)\}\) is turned into some \(\{(e^{2ik'\pi/3},v)\}, u,v \in \{1,-1,i,-i\}\) indexing the two triangles. By rotating the second component without changing the first (i.e., just rotating \(v\) to \(u\)), we can turn \(T_2\) back into \(T_1\), so \(T_1\) is fixed as a set. Next we fix all points of \(T_1\) by applying the appropriate isometry of the first dihedral group (i.e., just moving the \(e^{2ik\pi/3}\) around). We now have an isometry which fixes the first component. Since it is isometric in \(\mathbf{C}_2\), it induces an isometry of the second component, which describes a square. By applying the inverse isometry which lies in the second dihedral group \(D_4\) (i.e., moving around the four \(e^{2i\ell\pi/4}\)), we fix all 12 pcs. Any isometry of \(\mathbf{C}^2\) which fixes these 12 points must be the identity.
[37] We have proved that our initial isometry, when composed with some appropriate combination of the 48 isometries listed previously, is reduced to identity. This proves that this isometry is the product of their inverses, e.g., a member of the 48-element subgroup, and hence that this subgroup comprises the whole group.
3.2 Proof of Theorem 2 on Affine Transforms
[38] We make explicit the isomorphism between \(\mathbf{Z}_3 \times \mathbf{Z}_4\) and \(\mathbf{Z}_{12}\), e.g., \[ \Phi: (a,b) \mapsto 4a - 3b\ \mathit{mod}\ 12 \quad \text{ and conversely } \quad \Phi^{-1}(x)=(x\ \mathit{mod}\ 3, x\ \mathit{mod}\ 4) \] One can easily confirm that this makes sense (\(a\) (respectively \(b\)) being defined modulo 3 (respectively 4), \(4a\) (respectively \(3b\)) being defined modulo 12) and is an injective group morphism, bijective since both groups on either end have the same cardinality. Finally, \[ (4a-3b\ \mathit{mod}\ 3, 4a-3b\ \mathit{mod}\ 4) = (a,b) \in \mathbf{Z}_3 \times \mathbf{Z}_4 \]
[39] Now the T/I group is generated by transposition \(t:x \mapsto x+1\) and inversion \(i:x\mapsto -x\), which are turned by \(\Phi\) into \[ \text{T}_1: (a,b) \mapsto (a+1,b-1) \qquad \text{I}_0:(a,b) \mapsto (-a,-b) \] This generates the group of transforms \((a,b) \mapsto \pm(a-k\ \mathit{mod}\ 3,b+k\ \mathit{mod}\ 4),k \in \mathbf{Z}_{12}\), a group with 24 elements.
[40] The new elements which are neither transpositions nor inversions change orientation, e.g. \((a,b)\) turns into either \((-a,b)\) or \((a,-b)\). Thus the whole group is made of transforms \[ (a,b) \mapsto (\pm a-k,\pm b+k), k\in \mathbf{Z}_{12} \] with independent signs for \(a,b\). In \(\mathbf{Z}_{12}\), if we drop the arbitrary transposition factor \(k\) for clarity, we have the correspondence shown in Table 1, since, for instance, \(5 \times (4a - 3b\ \mathit{mod}\ 3,4a-3b\ \mathit{mod}\ 4)=(20a\ \mathit{mod}\ 3,-15b\ \mathit{mod}\ 4)=(-a,b)\).
We have recovered exactly the \(4 \times 12=48\) affine transformations in \(\mathbf{Z}_{12}\).
3.3 Proof of Theorem 3 on Affine Transforms and Shape
[41] It is sufficient to reduce the hypothesis to the preservation of dyads, i.e., we assume that \(\sigma\) is a permutation of \(\mathbf{Z}_n\) such that for any dyad \((a,b)\) with interval class \(i=|b-a|\), the image dyad always spans the same interval \(j=|\sigma(b)-\sigma(a)|\). For instance, any semitone is always turned into a fifth or fourth.
[42] Consider dyad (0,1) and let its image be \((\sigma(0),\sigma(1))=(\alpha,\beta)\) with \(\beta - \alpha = \delta\). Consider also dyad (1,2) with image \((\sigma(1)=\beta,\sigma(2)=\gamma)\): if we work with orbits under T only, then necessarily \(\gamma - \beta = \delta\) too. If we work with T/I, then the interval could be reversed, i.e., \(\gamma - \beta = -\delta\). But since \(\beta - \alpha = \delta\) this would lead to \(\alpha=\gamma\) and \(\sigma\) would no longer be bijective.
[43] Hence \(\sigma(2)=\gamma=\gamma-\beta+\beta-\alpha+\alpha=\alpha+2\delta\). Similarly or by easy induction, \[ \sigma(k)=\alpha+k\delta \] (identifying \(k\in \mathbf{Z}\) and its class modulo \(n\)).
[44] This is an affine map. Since \(\sigma\) is bijective, it is necessary and sufficient that \(\delta\) be invertible in \(\mathbf{Z}_n\), and hence we have an affine transformation.
Emmanuel Amiot
Associated Researcher to LAMPS
Perpignan University
manu.amiot@free.fr
Gilles Baroin
Laboratoire MAIAA, ENAC (École Nationale de l’Aviation Civile)
Laboratoire LLA Créatis
Université de Toulouse, France
Gilles@Baroin.org
Works Cited
Baixas, Guillaume. 2012. “Etude des isométries du Model-Planet, un modèle de représentation des notes de musique.” Master’s thesis, Montpellier 2 University.
Baroin, Gilles. 2011a. “The Planet-4D Model: An Original Hypersymmetric Music Space Based on Graph Theory.” In MCM 2011: Proceedings of the 3rd International Conference on Mathematics and Computation in Music, 326–29. Springer.
—————. 2011b. “Applications de la théorie des graphes des objets musicaux. Modélisations, visualisations en hyperespace.” PhD diss., University of Toulouse le Mirail.
Cohn, Richard. 1991. “Properties and Generability of Transpositionally Invariant Sets.” Journal of Music Theory 35 (1–2): 1–32.
—————. 2012. Audacious Euphony: Chromatic Harmony and the Triad's Second Nature. Oxford University Press.
Fiore, Thomas, Thomas Noll and Ramon Satyendra. 2013. “Morphisms of Generalized Interval Systems and PR-groups.” Journal of Mathematics and Music 7 (1): 3–27.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
Mazzola, Guerino and Moreno Andreatta. 2007. “Diagrams, Gestures and Formulae in Music.” Journal of Mathematics and Music 1 (1): 23–46.
Mazzola, Guerino. 2002. The Topos of Music. Birkhäuser.
Peck, Robert, 2011. “Nth Roots of Pitch-Class Inversion.” MCM 2011: Proceedings of the 3rd International Conference on Mathematics and Computation in Music, 196–206. Springer.
Popoff, Alexandre. 2013. “Building Generalized Neo-Riemannian Groups of Musical Transformations as Extensions.” Journal of Mathematics and Music 7 (1): 55–72.
Rahn, John. 1980. Basic Atonal Theory. Schirmer.
Zacharias, Svatopluk and Daniela Velichova. 2000. “Projection from 4D to 3D.” Journal for Geometry and Graphics 4 (1): 55–69.
Footnotes
1. An isometry is a transformation that preserves distances.
Return to text
2. The authors thank Moreno Andreatta for raising the issue of the new isometries, Guillaume Baixas for his master’s thesis describing the whole group (Baixas 2012), and David Clampitt and the anonymous reviewers for their helpful comments and critiques.
Return to text
3. Visually, \(\mathbf{Z}_3\), \(\mathbf{Z}_4\), and \(\mathbf{Z}_{12}\) are cyclic graphs, not groups. Their group structures only appear as rotations of the sets, and we embed them in the larger, non-commutative groups of isometries in \(\mathbf{R}^4\) in the last section of this article.
Return to text
4. The pair (1, 1) represents
Return to text
5. In the original model (Baroin 2011a and 2011b), factors of \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{2}}\) respectively are applied in order to scale all edges to unit size, but this does not change the isometry group studied below. We will retain the simpler model given here since it provides a better and easier understanding of the algebraic situation.
Return to text
6. The 4D polytope is a geometrical object with vertices, edges, and faces like a cube or a dodecahedron, but in 4D space.
Return to text
7. The model is drawn on the torus \(T^2=S^1 \times S^1\) defined by \({(z,z') \in \mathbf{C}^2,|z|=|z'|=1}\), which is itself part of the sphere defined by equation (\(S\)). Thus an isometric embedding of the torus of thirds in 4D space is achieved.
Return to text
8. We thank Guerino Mazzola for permission to use his image.
Return to text
9. The matrix is truncated from a 4×4 orthogonal matrix and has the form \(\begin{pmatrix} -\sin(t) & \cos(t) & 0 & 0 \\ -\cos(t)\sin(u) & -\sin(t)\sin(u) & \cos(u) & 0 \\ -\cos(t)\cos(u)\sin(v) & -\sin(t)\cos(u)\sin(v) & -\sin(u)\sin(v) & \cos(v) \end{pmatrix} \) as discussed in Zacharias and Velichova 2000, which argues for the effectiveness of orthographic projections.
Return to text
10. An isometry is sometimes called a “rigid motion” because of its distance-preserving properties. While transpositions or rotations can be represented in any given dimension as continuous gestures, in order to represent inversions or reflections as continuous gestures, an additional dimension is required. For example, transposition of a trichord can be visualized as rotating a triangle on the circle of the pc clock face, but inversion (or reflection) requires flipping the triangle, a rigid motion. In order to visualize inversion as a continuous gesture, you have to give the circle another degree of freedom—i.e., another dimension, and rotate it embedded in 3D space.
Return to text
11. R, the relative transformation, inverts a major or minor triad preserving its major third as common tones; L, the Leittonwechsel transformation, inverts a major or minor triad preserving its minor third as common tones.
Return to text
12. This is reminiscent of Robert Peck’s search for the roots of inversions (Peck 2011): the example provides a square root of a major-third transposition, which is not a whole-tone transposition.
Return to text
13. The torus has first to be flattened on a plane, like pizza dough, and mentally prolonged periodically, both horizontally and vertically.
Return to text
Copyright Statement
Copyright © 2015 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
9904