Xenakis’ Sieve Theory: A Remnant of Serial Music?*
José L. Besada
KEYWORDS: sketch studies, Iannis Xenakis, twelve-tone music, sieve theory, algebra
ABSTRACT: Iannis Xenakis sternly criticized serial music in the mid-fifties. In response, he proposed and developed a set of compositional procedures which were mainly based on probabilistic laws that he framed under the principle of indeterminism. The sieve theory he developed in the sixties represented a return to deterministic strategies for composing. Following examination of Xenakis’ notes and sketches from the period spanning his time auditing Messiaen’s classes to his composition of Nomos Alpha, I argue that sieve theory is better understood when viewed through the lens of his personal earlier speculations on twelve-tone music techniques.
DOI: 10.30535/mto.28.2.2
Copyright © 2022 Society for Music Theory
Introduction
[1.1] Serialism, with its multiple variants, became a major compositional trend for art music in Western Europe during the fifties. It remained largely influential until at least 1958; John Cage’s arrival at the Darmstadt courses probably marked the end of its centrality (Iddon 2013, xi). Some problematic issues associated with serialism had already been targeted by several composers in this decade, mainly concerning its aural comprehensibility. Roberto Gerhard (1952) for instance, who studied with Arnold Schoenberg in the twenties, acknowledged a gap between the compositional strategies with twelve-tone rows and the listener’s experience. György Ligeti (1958), a composer situated well outside of the Schoenbergian tradition, provided one of the most authoritative critiques of the serialization of rhythmic figures, arguing that they are perceptually unequal to the manipulations of pitch rows. Other critiques quickly spread(1), with one of the most severe objections uttered by Iannis Xenakis (1955) in his famous article “La crise de la musique sérielle”:
Linear polyphony destroys itself by its very complexity; what one hears is in reality nothing but a mass of notes in various registers. The enormous complexity prevents the audience from following the intertwining of the lines and has as its macroscopic effect an irrational and fortuitous dispersion of sounds over the whole extent of the sonic spectrum. There is consequently a contradiction between the polyphonic linear system and the heard result, which is surface or mass (translated in Xenakis 1992, 8).(2)
[1.2] This short text provoked quarrels with peers such as Pierre Boulez (Varga 1996, 29), but above all, led Xenakis to publicly suggest, for the very first time, the possibility of using probabilistic laws as a useful tool in the field of composition, which he later linked to the notion of indeterminism (Xenakis 1961).(3) It was at the moment that Dimitris Exarchos (2019) has described as the beginning of Xenakis’ mid-period style that the Greek composer began to develop his sieve theory. This technical approach, which was first presented within a short essay in the mid-sixties (Xenakis 1965), should be regarded as his most deterministic contribution to music theory and composition. The composer openly addressed the question of determinism in his next technical essay about sieve theory (Xenakis 1966) and mentioned again the issue in the following years (Xenakis 1967; 1968), but mostly neglected this topic in the two texts on this issue he published significantly later (Xenakis 1988; 1990).
[1.3] In this article, I aim to observe sieve theory through the lenses of several serial techniques. By comparing some of Xenakis’ sketches and notes, I will highlight important coincidences between the speculative work he did on twelve-tone rows in the early fifties and the struggle with algebra which led him to finally develop the core concepts of his sieves. My hypothesis is that Xenakis’ experience with twelve-tone music might have been decisive for paving his way to reconsider some deterministic strategies for composition.
[1.4] First, I provide a brief discussion of the notions of determinism and indeterminism which are found in some of Xenakis’ writings. It is hoped that offering this prelude to the main argumentation will help avoid potential misconceptions with alternative uses of these terms by other composers or in some specific contexts of music theory. Second, I review the current knowledge of the approach and occasional uses of serial techniques by Xenakis before he openly rejected this compositional trend. Third, I discuss in detail the content of one of Xenakis’ notebooks in which he made several speculations about twelve-tone rows. To the best of my knowledge, the content of this notebook has not been discussed before. Fourth, and guided again by some of his manuscripts, I describe Xenakis’ endeavor with algebra in the sixties that finally resulted in the birth of sieve theory. The main theoretical features of his sieve theory are summarized there. Fifth, I confront the theoretical abstractions in the two previous sections, in order to synthesize all foregoing evidence in support of my hypothesis. Finally, I return to Xenakis’ position against serialism in the fifties in order to provide a historical recontextualization of the topic in the light of my previous discussion.
Xenakis on determinism and indeterminism
[2.1] Neither the term determinism nor indeterminism appears in Xenakis’ early critique of serial music. This does not mean, however, that he failed to note elements closely tied to these topics: his article characterizes serial rows, for instance, as “a linear arrangement (consecutive) of the twelve tones” or “a linear ‘category’ of thought” (Xenakis 1955, 2–3).(4) This short essay explicitly introduced at least the notion of harnessing probability in composition, an idea that was developed in further theoretical articles (Xenakis 1956; 1958; 1960). The concepts of determinism and indeterminism were first directly addressed in the aforementioned article in 1961, which was reworked for the initial chapter of his first monograph (Xenakis 1963, 15–56). In this essay, Xenakis stated that tonal music implies hierarchies in a “deterministic manner” related to “linear processes”; the Second Viennese School faced “the indeterminism of atonality” via twelve-tone rows which were “extremely casual in the strictest sense” (Xenakis 1992, 5). The problem arose, in his opinion, from the excessive complexity carried out by composers approaching serial techniques in the fifties (cf., quotation given in [1.1]). For Xenakis, “the strict, deterministic causality which the neo-serialists postulated was lost,” and, “[a]s a result of the impasse of serial music,” he decided to come with “a music constructed from the principle of indeterminism” (1992, 8).(5)
[2.2] While Xenakis’ remarks upon determinism and indeterminism in the previous quotes take into account the listener’s perception and expectations, he was more concerned with the degree of determinacy of the compositional strategies. Indeed, Xenakis labeled serialism as a particularly deterministic path mainly because of its underlying “linear arrangement” mentioned above, meaning the preexistence of a fixed order within a twelve-tone row. This categorization is akin to the definition of serial relationships that Milton Babbitt formulated when studying Igor Stravinsky’s late music. Henceforth, I will consider Babbitt’s definition as a theoretical background for the topics under discussion:
A serial relation is one which induces on a collection of objects strict, simple ordering; that is, an order relation which is irreflexive, nonsymmetric, transitive, and connected over the collection. The term “serial” designates nothing with regard to the number of elements in the collection, to the relations among these elements, or the operations—if any—applicable to the elements or the relations among them (1964, 39).
[2.3] In abandoning determinism, Xenakis did not embrace aleatoric music, in which process “is determined in general but depends on chance in detail” (Meyer-Eppler [1955] 1957, 55). In fact, his writings also denote an implicit criticism of post-Cagean compositional practices (Xenakis 1992, 180–81). Contrary to these compositional trends, Xenakis’ references to the term aleatory point towards the use of probabilistic formulae: these stochastic equations are clearly determined in his writings, mathematically speaking, but their mutable outcome is what leads to indeterminacy despite its musical transferring onto a score.
[2.4] Xenakis equally provided clearly determined formulae for his sieves, but, unlike the choice of probabilistic equations, their outcome is absolutely deterministic. This feature, in parallel with further theoretical speculations with finite groups,(6) is probably among the reasons that led him to reopen the discussion of determinism and indeterminism in his second essay on sieve theory (Xenakis 1966). In particular, when explaining some aspects of Nomos Gamma (1967–68), he highlighted the dialectics between the “deterministic and finite machinery” related to algebraic compositional perspectives—a category to which sieve theory belongs—and the “probabilistic and stochastic machineries” he previously conceived (Xenakis 1992, 237).
[2.5] Another pivotal concept for understanding Xenakis’ thought at this time is his distinction between in-time and outside-time categories of music. The composer presented these ideas in parallel for the first time with sieve theory (Xenakis 1965) and continued developing them after.(7) The outside-time category gathers, in the composer’s words, any musical structure “which is independent of temporal becomingness” (Xenakis 1992, 207). For instance, the concept of a major scale is outside-time while the pitch order of a twelve tone-row forces an in-time category.
[2.6] Taken together, Xenakis’ writings provided a demarcation of the boundaries between determinacy and indeterminacy both in general and with regard to his own compositional practices. He viewed that serial music was stuck in an impasse because of the contradiction between its deterministic orientation and its aural outcome. He consequently opted for a sophisticated approach in the fifties for introducing indeterminacy within his creative purposes, but in the sixties reconsidered again compositional strategies which he labeled as deterministic himself. As Xenakis studied and also occasionally resorted to serial techniques when he was young, it seems reasonable to explore whether these speculations with twelve-tone music may have had an impact—perhaps even an unconscious one—on his return to deterministic concerns.
The serial background: From the Bartókian project to Metastaseis
[3.1] Metastaseis (1954)(8) was the first of Xenakis’ pieces to garner significant reception, though it was not his first score. The majority of his early pieces, which remained unknown to the public for a long time, can be associated with his so-called “Bartókian project” (Solomos 2002, 22–26), which envisaged the inclusion of structural elements from the Greek oral traditions into new compositional ideas (Xenakis [1955] 2001). The largest and most sophisticated accomplishment to emerge from this project was his Procession aux eaux claires (1953), which was conceived as the opening of a triptych under the general title of Anastenaria. Xenakis managed to compose the last part of this triptych, which he entitled Sacrifice (1953), but never delivered the central score. Instead of finishing this project, he launched himself directly into the composition of Metastaseis.
[3.2] Sacrifice is a remarkably concise piece in terms of pitch distribution and rhythmic variety. Only the pitches E1, G2,
[3.3] Anne-Sylvie Barthel-Calvet has identified and described two medium-sized notebooks that were used by Xenakis when attending Messiaen’s classes. Among the many musical topics the Greek composer annotated in these notebooks, there are explicit references, dated in October 1953, to Anton Webern’s Drei Lieder op. 18 (1925), Zwei Lieder op. 19 (1926), and the Variationen für Klavier op. 27 (1935–36) (Barthel-Calvet 2012, 70). A few days after taking these notes, Xenakis began drafting an unfinished text entitled “Musique sérielle,” in which he pondered five balanced ways to split a twelve-tone row (Barthel-Calvet 2011, 5); this was probably inspired by Webernian methods (Barthel-Calvet 2012, 51).(11) Just a few months later, in 1954, Xenakis started to plan different compositional strategies for Metastaseis. After time spent struggling with potential twelve-tone rows in another notebook (Barthel-Calvet 2011, 6), he finally conceived of serial procedures—albeit sometimes defective ones (in terms of cardinality)—that were aimed at organizing, in different steps, a large central section of Metastaseis beyond its famous glissandi. These compositional strategies mainly focused on the interval relationships within the pitch-class sequences and their permutations, as well as on the connections with their related durations. Xenakis made his method explicit in a self-analysis that remained unpublished until the twenty-first century, when it was fully transcribed by Barthel-Calvet (2003, 162–87). In this text, he coined a number of serial neologisms, and schematized the intervals in a clock shape that somehow began his forthcoming pervasive use of visual diagrams for conceptualizing musical ideas (Solomos 2021). Some of these new concepts and the diagrams for distributing pitch classes were incubated in a document that I will discuss now.
Twelve-tone music speculations: The Anastenaria large notebook
[4.1] Xenakis’ interest in serialism covered a quite short time period, from Messiaen’s teaching about Webern’s music to the composition of Metastaseis, in which the above-mentioned chronological sequence seems to be strongly linked (Barthel-Calvet 2013, 189). Sketch studies, in general, have been pivotal for shedding light on this aspect of the composer’s career. There is, however, one item that, to my knowledge, has either gone unnoticed or been overlooked by the scholars dealing with Xenakis’ handwritten documentation of this period. This document, as will be shown, is essential for understanding how some twelve-tone techniques and sieve theory share substantial features. Consequently, in the following section I offer a thorough survey of this notebook.
[4.2] The majority of Xenakis’ compositional sketches are currently archived at his daughter’s home in large office boxes under the general label OM (Œuvres Musicales); each contains several folders. Box OM-2 is first and foremost designated for the composer’s sketches of his early musical works before Metastaseis. Folder 25, found within, houses an almost folio-size notebook with a beautiful Chinese-themed cover on which Xenakis wrote Anastenaria in Greek. He annotated the numbers 1 to 26 on the lower-right corner of the cover and the subsequent front pages. When referencing sheets, I will add the letters “f” or “b” when necessary to indicate front or back pages, respectively. In addition, a fragment of a sheet of translucent graph paper is kept inside the notebook. Despite the difference in material, it is plausible that Xenakis worked on this sheet at the same time as on the notebook, as its most relevant drawings are clearly connected to the content of the notebook; I will therefore consider the graph paper a constituent element of a common reflective process. Neither the notebook nor the attached sheet is dated. The most likely period for dating the content of folio-size notebook spans from Spring 1953 to the end of that year, probably fitting with its last months.(12)
Example 1. Page 13f of Xenakis’ Anastenaria folio notebook. © Xenakis’ family, reproduced by permission.
(click to enlarge)
[4.3] The content of sheets 1 to 8 is unrelated to twelve-tone music. The main annotations in these sheets lay out time durations and rhythmic figures in combination with numeric calculations which depend on values of the Fibonacci series. The issues concerning twelve-tone music begin on page 9f, where Xenakis transcribed the row of Schoenberg’s Variationen für Orchester op. 31 (1926–28). Schoenberg, and specifically a reference to his Klavierstück op. 33a (1928–29), is previously invoked in one of Xenakis’ early medium-sized notebooks, along with the date May 1952 (Barthel-Calvet 2012, 62). Note that this annotation does not appear in the medium-size notebooks, which are identified as those he used in Messiaen’s courses.(13) By contrast, the twelve-tone row for Schoenberg’s piano piece also appears on page 13f of the Anastenaria folio notebook (Example 1). It is therefore not possible to infer with certainty Xenakis’ source for Schoenberg’s rows.(14)
Example 2. Transcription of twelve-tone rows in the Anastenaria folio notebook: a) from Schoenberg’s Variationen für Orchester op. 31; b) from Schoenberg’s Klavierstück op. 33a; c) same as Nono’s row for Il canto sospeso; d) two confronted whole-tone scales
(click to enlarge)
Example 3. Transcription of the circled representations of rows in Xenakis’s Anastenaria folio notebook: a) from Schoenberg’s Variationen für Orchester op. 31; b) from Schoenberg’s Klavierstück op. 33a; c) same as Nono’s row for Il canto sospeso
(click to enlarge)
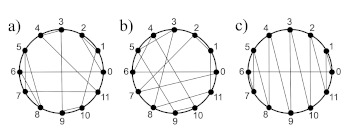
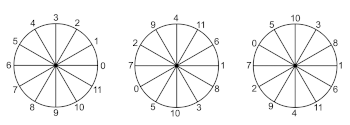
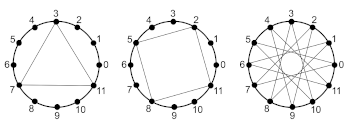
[4.4] The aforementioned twelve-tone rows appearing on page 13f of the Anastenaria folio notebook, plus two additional ones—along with pitch-classes names, integers, or both designations—are the only complete rows given in this document; see Example 2. Three of these four rows are also diagrammatically displayed on clockface diagrams within this page, with the 0 on their rightmost point and the arithmetic progression going through 11 unfolding counterclockwise. For each case, 0 stands as the first element of the twelve-tone row and the other numeric values represent the pitch classes obtained through the ascending interval with the same number of semitones. The closed polygon in any diagram connects the adjacent elements of a row, represented by big dots, as well as its extremes; see Example 3. Additional diagrams in this style are found in the notebook, along with calculations that ostensibly represent attempts to construct rows under certain conditions I discuss below.
[4.5] The four rows that are found in Xenakis’ manuscript share properties of hexachordal combinatoriality. Both of Schoenberg’s rows are semi-combinatorial: the others belong to the only six sets which are all-combinatorial.(15) Combinatorial properties are, of course, related to Xenakis’ interest in row partitions as expressed throughout his other manuscripts. The annotations in the folio notebook, however, take another path.
[4.6] Interestingly, one of Xenakis’ twelve-tone rows—A,
We can note first that, within the mass of 500 millions of rows, from a diastematic viewpoint, there must be a few ones with a very small number of different intervals. The chromatic scale would be an extreme case with the only interval +1. There is however a limited number of those [rows] that would have only twice the totality of intervals 1, 2, 3, 4, 5, and 6 in absolute value. [ . . . ] These rows differ from each other only by the arrangement of intervals (Xenakis transcribed by Barthel-Calvet 2003, 172).
[4.7] In the quote above, the term “diastematic” (diasthématique) alludes to intervals. We currently know that only 3856 all-interval rows exist (Morris and Starr 1974, 366).(18) Xenakis estimated, in terms of interval adjacency, several of them under certain initial conditions for Metastaseis (Barthel-Calvet 2003, 175–80). It is intriguing that Xenakis arrived on the concept of all-interval series independently, but is even more remarkable the question he formulated in reference to it, which is written on page 13f of the Anastenaria folio notebook:
Question ? Which are the interval sequences that provide me the total chromatic only?
Example 4. Transcription of Xenakis’ representation of the equivalence of semitones and perfect-fourth steps. The pitch names are in French in the original manuscript
(click to enlarge)
Example 5. From left to right, transcription of Xenakis’ circles of consecutive semitones, perfect fourths, and perfect fifths
(click to enlarge)
[4.8] An all-interval twelve-tone row is a dodecaphonic sequence that contains all of the pitch-class intervals. Xenakis was dealing with the same issue, but doing so in opposite terms: for him, the starting point was the set of all intervals, and the way to organize them for retrieving the totality of pitch classes. This distinction may seem slight, but is meaningful for arguments I will provide in further sections.
[4.9] As suggested above, the topic of all-interval twelve-tone rows brings Berg’s music to mind. Further aspects of the folio notebook resonate with the Austrian composer. On page 10f there is a linear representation of pitch classes wherein the integers are related to pitches in the upper section (Example 4). Below, the numeric values are reordered in intervals of perfect fourths. As both orders generate all integers from 0 to 11, this representation puts into evidence how Xenakis found by himself that a cycle of fourths is isomorphic to a chromatic scale. He transferred this idea to circular templates on pages 10f to 11f; these are similar to those previously shown, but represent cyclic perfect fourths and fifths (Example 5). The isomorphism of the cycle of semitones and the one of major sevenths is a basic notion of twelve-tone music, as it matches with the idea of inversion. In turn, the isomorphism with the cycles of perfect fourths and perfect fifths was exploited by Berg, for instance, in his opera Wozzeck (1914–22) (Perle 1977a).(19) This procedure was brought to light by Ernst Krenek (1937, 77), and the underlying idea is currently identified in post-tonal music theory with the notion of modular transformation.(20)
Example 6. Transcription of Xenakis’ interval multiplication of a melodic contour
(click to enlarge)
[4.10] Xenakis did not apply these kinds of transformations to the twelve-tone rows he wrote in his notebook. Nevertheless, on page 8f, just before starting to transcribe the aforementioned twelve-tone rows, he drafted a short melodic excerpt consisting of four pitches, which he transformed into two new profiles by multiplying its intervals by 2 and 3 (Example 6). Besides, in a passage on this page dealing with values 2, 3, 4, and 6, he highlighted that their related intervals “do not provide the aggregate”. In sum, Xenakis was thinking in terms of interval multiplication, although he did not factually manipulate any twelve-tone row with these techniques.
Example 7. Excerpt of Xenakis’ translucent graph paper which is kept inside the Anastenaria folio notebook. © Xenakis’ family, reproduced by permission
(click to enlarge)
Example 8. Unpacking of circled polygons in Xenakis’ translucent graph paper
(click to enlarge)
[4.11] There are yet more aspects of the clockface diagrams in the Anastenaria folio notebook that are of interest. For instance, the reason for choosing the rightmost point of the circle and moving counterclockwise is revealed on page 18f: the circle served him in exploration of trigonometrical functions, an attempt that was ultimately discarded. Another rejected shape is a division of the circle into 24 parts, as shown on page 17b. Manipulations of the Archimedes spiral are found on sheet 19, but its most accomplished representation is drawn on the translucent graph paper accompanying the notebook (Example 7); the representation is quite akin to Roger Shepard’s pitch helix (1965, 104). On the right of his spiral, Xenakis drew again a clockface diagram and outlined several polygons on both sides of the translucent paper. These forms can be split into an equilateral triangle, a square, and a dodecagram (Example 8). The triangle represents the pitch-class set of an augmented triad, the square stands for a diminished seventh, and the dodecagram is isomorphic to the circle of perfect fourths Xenakis drew on the notebook. In doing so, he was visually representing how the minor and major thirds generate defective subsets with regard to the aggregate whereas the perfect fourth—alternatively the perfect fifth—is a generator of all the pitch classes.
[4.12] Many of Xenakis’ speculations that I have discussed when viewed in our present context might be seen as constituting relatively basic music theory knowledge. However, it is important to stress the intellectual value of his approaches to interval cyclicity and permutability through mathematical abstraction, particularly when remembering first, their novelty at the time he developed them, and second, that he did not follow an orthodox path of compositional training. I highlight this fact as it will have consequences in the following sections of my article, in which I discuss Xenakis’ more explicit uses of algebraic notions and operations.
The algebraic endeavor: From Herma to Nomos Alpha
[5.1] After Metastaseis, Xenakis’ output in the fifties includes some of his most emblematic pieces based on stochastic laws, namely Pithoprakta (1965) and Achorripsis (1956), as well as his first explorations in the world of electronics with Diamorphoses (1957) and Concret PH (1958). Starting with Herma (1960–61), Xenakis combined his stochastic methods with a new focus on Boolean algebra. He published an essay in his first French monograph which summarizes the main mathematical features of this piano piece (Xenakis 1963, 181–208). In particular, he mentioned that the distribution of pitches in this score depends on three non-disjunct subsets that are playable on a piano; these subsets were “chosen a priori” because of “a characteristic property” (Xenakis 1992, 170). The property is not highlighted at all in the essay; however, Xenakis’ archived documents concerning the piece, which are found in folders 17 to 29 of box OM-12, may shed some light on this topic. Indeed, some annotations on sheets 1 and 2 of folder 22 suggest a probabilistic method for distributing intervals in different registers of the referred subsets.
[5.2] The pitch content of these initial subsets was most likely derived from stochastic calculations. The formal manipulations Xenakis carried out with them, however, are absolutely deterministic, as he took advantage of three basic Boolean operators: the union, the intersection, and the complementarity. The union merges all the pitches from the involved sets, the intersection selects only the pitches which are present in all the starting sets, and the complement of a set is the one gathering all the pitches which do not belong to this former set. The determinism of these Boolean operations does not necessarily imply that their outcome must be aurally perceivable. In this sense, it has been pointed out that Herma could fall under the same criticism that Xenakis enounced against serialism (Wannamaker 2001, [5.4]),(21) a remark with which I agree. Further, it is possible that the conceptual contradictions surrounding the inception of this piano piece simply reflect a moment in which its author was struggling to incorporate explicit algebraic elements within his compositional practices—in particular, his efforts to conceptually delimit what he labeled later as an outside-time category (Exarchos 2019, 26).
[5.3] The essay presenting Herma was not the first time Xenakis alluded to algebra in his writings, but it does stand out for its level of detail and in its development of a precise terminology borrowed from this field of mathematics. Various documents leading to the composition of this piano piece and its related theoretical essay are kept in Xenakis’ archives. Among them, folder 22 of box OM-12, is particularly relevant. This folder gathers eight loose but numbered notebook sheets that were once stapled together. Page 4b of this document explores the issue of binary relationships between pairs of elements of a set, using for this purpose the notation a, b, and c for the elements and E for the whole set. Near the end of the page, Xenakis wrote the following lines:
This relation [\(R\)] is of equivalence because
- \(aRa\) for every \(a \in E\) (reflexivity)
- \(aRb\) always entails \(bRa\) (symmetry)
- \(aRb\) and \(bRc\) entail \(aRc\) (transitivity)
\(a\) and \(b\) are said congruent
\(a \equiv b\) (modulo \(R\))
[5.4] The lines above basically provide the definition of an algebraic equivalence relation, with the notion of congruence intrinsic to it. Whereas reflexivity, anti-symmetry, and transitivity had already been mentioned by Xenakis (1963, 188) when analyzing Herma, the issue of congruences was not yet developed at all. Prototypic congruences and their standard notation—through the symbol ≡ indicated above—were introduced by Carl Friedrich Gauss at the beginning of the nineteenth century when he established a basis for modular arithmetic. Neither this symbol nor the notion of congruence is traceable, to my knowledge, in Xenakis’ published articles prior to the composition of Herma. By contrast, the notation for modular arithmetic is found in the Anastenaria folio notebook on page 12b, just past the circles with different interval steps and before the discussion of all-interval twelve-tone rows:
- I admit that there are only 12 different sounds in all the sound spectrum.
- From a sound, I can find the other 11 ones by adding semitones (≡ unit) and retrieve at the octave (≡ +12 semitones) the initial sound.
- I can go counterclockwise by subtracting semitones.
- Image of the circular period 12 sounds ≡ 2π.
- As it is not the positive or the negative interval what interests me but the sound itself, the expression of these constants is made through circular functions.
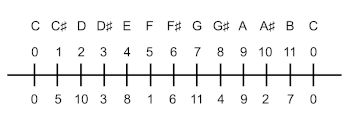
[5.5] Points 1 to 3 mainly summarize the modular arithmetic behind the notion of pitch classes. Indeed, Western equal temperament induces an organization of pitches which, since a specific one becomes the referential point, is isomorphic to the set of integers. The principle of octave equivalence in atonal music theory—specifically in the case of twelve-tone music—matches with partitioning the set of integers into 12 quotient classes by means of a modular congruence. Consequently, the set of 12 pitch classes is isomorphic to the cyclic group of 12 elements which may host diverse arithmetic operations modulo 12.
[5.6] Xenakis did not truly connect these algebraic issues with twelve-tone music concerns in his writings of the fifties and early sixties.(22) His most thorough effort on harnessing algebraic notions for compositional purposes dates from October 1963 to September 1964, when he stayed in Berlin with an artistic grant awarded by the Ford Foundation and the West-Berlin Senate. The birth of his sieve theory can be dated precisely as occurring in this period (Exarchos 2019, 33). He presented the most important results stemming from his theoretical speculations with algebra a few years later, in an essay specifically connected to Nomos Alpha (1966) (Xenakis 1967).(23) The analysis in that text demonstrates how he took advantage of non-commutative groups—the rotations of polyhedrons—for conceptualizing the form of his score. The essay also comments on the use of cyclic groups for implementing a sieve of pitches. The intriguing complexity of Xenakis’ essay has surely enhanced the interest that several scholars have shown in this cello piece (Vandenbogaerde 1968; DeLio 1980; Vriend 1981; Solomos 1997; Peck 2003). Sieves were implicitly defined in Xenakis’ mentioned article as follows:
Since we are dealing with a sieving of the basic scale (elementary displacement by one semitone), each residual class forms a sieve allowing certain elements of the chromatic continuity to pass through. [ . . . ] Starting from [ . . . ] elementary sieves we can build more complex scales—all the scales we can imagine—with the help of the three operations of the Logic of Classes: union [ . . . ], intersection [ . . . ], and complementation (Xenakis 1992, 196).
[5.7] Xenakis’ articles in the sixties stand as fair presentations of his results, hence do not reflect the conceptual endeavor the composer accomplished through several years. His efforts can be better understood in the context of a number of sketches he drafted during these years. Box OM-19 in Xenakis’ archive gathers a number of folders with the speculations he formulated in Berlin, aimed at introducing several algebraic models for composition. Box OM-12—i.e., the same in which the documents for Herma are found—houses the folders with the preserved sketches and self-analytical documents related to Nomos Alpha.
[5.8] It is not my aim to describe these sketches with the same detail I provided for the Anastenaria folio notebook, as this task has been already done, mainly concerning the most abstract aspects of Xenakis’ speculations with group theory (Exarchos 2019, 28). Nevertheless, some of these drafts deserve attention, not only in the interest of establishing chronology, but for introducing the fundamental concepts of sieve theory. This technique, applied to pitches, serves for calculating sets generated by a periodic interval—any of these is an elementary sieve—which are subsequently manipulated by means of Boolean operations. In doing so, the resultant sieve is a much more complex pitch reservoir which hides local interval periodicities. The examples below illustrate this fact.
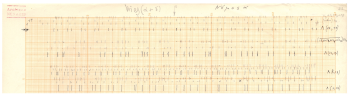
Example 9. Fragment of Xenakis’ graph paper for representing pitches of the three main sets for Herma; below, the visual outcome of some the derived sets from some Boolean operations with the former ones. © Xenakis’ family, reproduced by permission
(click to enlarge)
[5.9] Xenakis routinely took advantage of the grids on graph paper for proportionally visualizing pitches and time events as well as their related distances, respectively intervals and durations. Similar horizontal linear distributions of vertical short pen marks standing for pitches are found, for instance, among the sketches for Herma (Example 9), the first sieving attempts within the documentation generated during the artistic stay in Berlin (Example 10), and the sketches for Nomos Alpha (Example 11).
Example 10. Fragment of Xenakis’ graph paper for estimating pitches, derived from elementary sieves modulo 12 and 10. © Xenakis’ family, reproduced by permission. (click to enlarge) | Example 11. Fragment of Xenakis’ graph paper for estimating microtonal pitches for Nomos Alpha, derived from complex sieve operations. © Xenakis’ family, reproduced by permission. (click to enlarge) |
[5.10] Example 9 will serve to illustrate how to read these sketches. As stated in paragraphs [5.1-2], pitch sets—named A, B, and C by Xenakis—for Herma were ostensibly obtained via stochastic methods, which may explain the unpatterned distribution of marks on the paper. Considering only the pen marks which are aligned on the left of letter B, it is possible to read the
[5.11] The alignments of horizontal pen marks in Example 10 are by contrast quite predictable due to their periodicity. Here, the referential 0 marked in the upper edge stands for a particular C, and each small square stand for a semitone. On the upper left, the composer wrote 1M12, 5M12, 7M12, and 11M2, which may be read as the sets of integers 1, 5, 7, and 11 modulo 12. Each expression matches with an elementary sieve. For instance, 1M12 is the numerical set \(\{\ldots, -23, -11, 1, 13, 25, 37, \ldots\}\), which leads to an octave repetition of
[5.12] Unlike the other fragments I have reproduced, the graph paper for Nomos Alpha in Example 11 includes no pitch names, and is again quite unpredictable, visually speaking. Algebraic formulations of some elements of the sieve are expressed this time on the right, but these schemes are unfortunately less meaningful for comparison with the previous images. The reason is that the sieve for the cello piece was used by Xenakis for filtering a nonequal microtonal distribution of pitches, which differs from the distribution of 12 semitones in equal temperament. Sieves are abstract expressions of modular arithmetic that can be remapped onto different partitions of the octave, even those which are not equal (Xenakis 1992, 195). I will, therefore, remap some of his sieves for Nomos Alpha, his first piece in which complex sieves were exploited, onto the standard pitch distribution in order to demonstrate his compositional method. Xenakis (1992, 230) labeled the following expression as his “departure function” for the cello score:
$$ L(11,13)=[(\overline{13_3 \cup 13_5 \cup 13_7 \cup 13_9}) \cap 11_2] \cup [(\overline{11_4 \cup 11_8}) \cap 13_9] \cup 13_0 \cup 13_1 \cup 13_6 $$Example 12. Remapping of Xenakis’ sieve L(11, 13) for Nomos Alpha onto the piano keys, preceded by its elemental constituents
(click to enlarge and see the rest)
[5.13] Here, any elementary sieve \(b_c\) has to be read as c modulo b; it replaces the previous notation cMb in Example 10. For instance, \(13_3\) gathers the values congruent with 3 modulo 13, leading to the subset of integers \(\{\ldots, -23, -10, 3, 16, 29, 42,\ldots\}\). Unions and intersections are represented with the standard mathematical notation, and complementarity is designed with an upper line. Considering value 0 as the lowest C of the piano and ignoring the negative numbers of the whole sieve, it is quite straightforward to musically map the departure function onto the keyboard pitches; see Example 12 for a more straightfordward discussion in the next section.(24)
Example 13. Remapping of Xenakis’ sieve L(13, 11) for Nomos Alpha onto the piano keys
(click to enlarge)
[5.14] In addition to the departure function, Xenakis conceived metabolae, a technique in which the numeric values representing each elemental expression of the sieve are modified while the operational structure is preserved. In particular, he highlighted that a variation of the sub-indices induces transposition, and described the change of moduli with the term modulation (Xenakis 1992, 199). The following expression comes from multiple metabolae of the departure function for Nomos Alpha (Xenakis 1992, 231), producting a different set of pitches when mapped again onto the keyboard frame (Example 13):
$$ L(13,11)=[(\overline{11_2 \cup 11_4 \cup 11_7 \cup 11_9}) \cap 13_0 ] \cup [(\overline{13_5 \cup 13_10}) \cap 11_9 ] \cup 11_1 \cup 11_2 \cup 11_4 $$[5.15] Sieve theory gathers even more subtleties, but all the elements I have identified are enough for further discussion. In particular, some specific cyclicities and the modular transformations related to Xenakis’ metabolae will be crucial for the comparison of sieve theory and his former interest in twelve-tone rows that I provide at the end of the following section.
Discussion: Sieves, twelve-tone rows, and amnesia
[6.1] The two sieves above along with their musical mappings are not meant to serve as extensive theorizations about the algebraic intricacies of Xenakis’ creative method. That endeavor has already tackled by other scholars (Jones 2001; Gibson 2002; Exarchos 2007).(25) My aim in this section is simply to note the implications of the use of sieves for obtaining pitch sets against Xenakis’ efforts in the early fifties to extract useful elements from twelve-tone techniques.
[6.2] As such, the current representation of the sieves in Examples 12 and 13 require further consideration both in numerical and pitch terms, and are therefore not meaningful enough yet. It is valuable to represent them as interval arrays, i.e., the ordered list of adjacent intervals (Chrisman 1977), which leads to the following numeric sequences, respectively, for L(11, 13) and L(13, 11):
1-1-4-3-4-1-5-3-2-2-1-5-3-4-1-5-7-1-5-3-4-1-5-7-1-5
1-1-2-5-3-1-2-5-3-1-2-8-1-2-2-3-3-1-2-4-1-3-1-2-5-1-2-1-2-8-1-2
[6.3] This representational system was also exploited for analyzing two piano pieces in which Xenakis drew upon sieves for managing the distribution of pitches (Squibbs 2002, 92; 2003, 134). Squibbs’ articles reproduce the following interval arrays, the first one concerns Mists (1980) and the second is related to à r. (Hommage à Ravel) (1987):
2-6-2-3-3-5-2-4-3-6-2-3-2-1-5-2-1-5-1-4-4-2-3-1-4-3-2-4-2-(3)(26)
2-1-1-3-2-1-3-1-2-1-4-2-2-4-1-2-2-1-3-1-4-1-3-1-4-1-4-1-1-3-1-3-1-2-3-1-4-1-4-4-1-1
[6.4] Two important features are shared by all of the interval arrays above. First, they are not cyclical within the boundary the keyboard imposes.(27) Each one of Xenakis’ sieves is a limited chain of operations over a finite number of elemental congruences, which leads to a trivial consequence: the least common multiple of all the modular bases equals the sum of all the intervals of the cyclical interval succession generated by the whole sieve. In the case of the two sieves from Nomos Alpha, 11 times 13—143—is larger than the number of keys on a piano, a value that hides the cyclicity of the sieve. In particular, a least common multiple other than 12 or any of its divisors entails the emergence of a non-octave repeating reservoir of pitches. Second, the intervals of the array are quite varied and unpredictable in absence of the underlying formulae, although some general trends may be identified, such as small intervals appearing more often than large ones.
Example 14. Fragment of Xenakis’ graph paper for estimating pitches, derived from congruences modulo 15. © Xenakis’ family, reproduced by permission
(click to enlarge)
[6.5] In spite of the non-octave repetition and the unpatterned distribution of intervals in the previous examples, Xenakis frequently used quite standard pitch scales for introducing the topic of sieves in his writings; Messiaen’s modes of limited transposition served as an ideal example for him. With respect to the principle of octave repetition, he did not deeply explore the properties of intervallic patterns for pitch systems wherein this principle fails to apply.(28) With respect to the distribution of intervals, he sometimes summoned different historical scale systems but did not consider at all important features which lead to their interval equilibrium, such as the modern concept of well-formed scales (Carey and Clampitt 1989).(29) I contend that the construction of scales was not truly problematized in Xenakis’ texts, but served rather for introducing his sieve theory through useful examples that may have arisen as byproducts during his attempts to deal with modular arithmetic. The octatonic scale, which matches with Messiaen’s mode 2 and its alternation of tones and semitones, is a good example of problematizing this issue. This scale almost emerged in his Berlin drafts on graph paper when he started to calculate the union of some basic congruences (Example 14). This union can be expressed mathematically as the following assembly of elementary sieves:
$$ S=15_1 \cup 15_2 \cup 15_4 \cup 15_7 \cup 15_8 \cup 15_{11} \cup 15_{13} \cup 15_{14} $$[6.6] The formula above describes the union of all the sieves in which every representative of each elementary sieve is coprime with respect to modulo 15—i.e., both numbers do not share a positive divisor other than 1. It is not a complete mapping of the octatonic scale, as happened in Example 10 with the whole-tone scale, but its content is equivalent to this scale in terms of pitch-class set. A fully unfolded octatonic scale admits a much more simple and compact formulation via sieves, for instance \(3_0 \cup 3_1\). Although there is no explicit mention of Messiaen’s modes in the sheet containing Example 14, Xenakis was aware of the pitch-class content of this sieve, as it is shown in the “minus {C,
For me, these modes of limited transposition were modes like others, as any we can build. Only one thing haunted my mind, the fact that he named them “of limited transposition”. [. . . ] After, I told myself, why not inventing too? I reflected a lot about a more theoretical approach [. . . ] based on logic operations and wrote Herma [. . . ]. But I felt that the introduction of probabilities I did was not enough and it was just a first attempt, a deeper dialectic of order and disorder was needed, etc. And I built sound classes for piano, and next [performed] logical operations with these classes.
Messiaen used his modes of limited transposition as a coloration above all [. . . ]. A scale may serve however to any feature of sound [. . . ], on condition that these features [. . . ] form an absolutely ordered set (Xenakis, quoted in Boivin 1995, 366–67).
[6.7] What shall we make of the fact that these utterances clash with the lack of evidence in the sketches above relating to Messiaen’s ideas, particularly against the backdrop of a sieve which matches with an octatonic scale in terms of their shared pitch-class set? It is important to remember here that composers’ a posteriori mental reconstructions of their compositional choices or theoretical reasonings often diverge significantly from their actual practices (Theureau and Donin 2006). My hypothesis is that Xenakis connected his sieves with Messiaen’s modes after he had already gained some experience with his technique. Perhaps this link biased his memories about the process, as no explicit reference is found in his first documented attempts in Berlin.
[6.8] The content of his auditor notebooks indicates that Xenakis learned about Messiaen’s modes at the Conservatory. Coincidently, he copied them in pages close to those which were used for annotating Messiaen’s analyses of Webern’s music (Barthel-Calvet 2012, 70). A further wrinkle at that time is that Messiaen also mentioned Ivan Wyschnegradsky’s oeuvre, which means that the idea of non-octave repeating scales (1972) might also have arisen in that manner. But Xenakis did not explicitly take advantage of this modal knowledge for his creative practices; it was, in fact, his speculations about twelve-tone music, as previously summarized, that helped him to write a section of Metastaseis. Several years later, he developed his sieves and provided explicit connections with tonal and modal scales in his theoretical essays about the topic. It is thus problematic to consider Xenakis’ music with pitch sieves as truly modal from an aural perspective, as he implemented them in very different ways.
[6.9] To conclude this section, I will connect the disparate elements treated earlier to show that important aspects of Xenakis’ sieves are akin to his younger reflections on serialism. In doing so, I am not suggesting that twelve-tone techniques serve as the singular, definitive germ of the sieve theory; doing this would be as reckless as drawing a direct link with Messiaen’s modes which I have characterized as his mental, a posteriori construct. I will show, however, that his speculations in the period with twelve-tone concerns and those associated with his work on algebraic operations have strong resemblances. My argument is that Xenakis’ former contact with serial music helped him to achieve insights with regard to pitch intervals of twelve-tone rows and potential operations with them that, consciously or not, were later reinjected in his conceptualizations for sieve theory. The following points support my assertion:
- Xenakis was aware of the existence of modular arithmetic well before he started to develop his sieves. The idea of implementing congruences with compositional purposes was already incubated in the documentation for Herma. The Anastenaria folio notebook incorporates passages sharing notational elements with this branch of algebra, which Xenakis borrowed for implicitly conceptualizing the notion of pitch classes.
- One of Xenakis’ main interests in the use of twelve-tone rows was an exploration of interval variety. He even considered the family of all-interval twelve-tone rows as a kind of serial category—in almost transformational terms—by itself, in the same way serial composers regarded transpositions and inversions as consistent operations. It should be remembered that Xenakis considered the intervals as the starting point for retrieving after the totality of pitch classes of an all-interval twelve-tone row. Xenakis’ sieves often generate sequences of pitches with interval arrays which are quite varied and locally unpatterned, unlike the self-evident cyclic interval content that generally structures modal music. The way he usually implemented this method tends to saturate the totality of pitch classes—i.e., to provide at least one representative of any pitch class—without an obvious patterned distribution. Examples of this condition are found in the aforementioned piano pieces in [6.3].
- The Anastenaria notebook shows how Xenakis realized that the coprime values of 12 and lower than it—i.e., 1, 5, 7, and 11—were the only intervallic generators of all possible pitch-classes. In other words, he was aware that the semitone, the perfect fourth, the perfect fifth, and the major seventh are the only intervals which may generate, by recursion, the twelve pitch classes. Years later, Xenakis paid special attention to sieves whose elemental congruences had coprime modular bases with respect to the overarching bases matching with the octave. These coprime integers are again responsible for a variety of underlying pitch classes for each elemental sieve. Indeed, pitch classes within these elemental sieves are not repeated in different octaves when they span through a relatively bounded register. This feature partially echoes to the avoidance of pitch-class repetitions in twelve-tone rows.
- An isomorphic mapping appears between a series of semitones and a sequence of perfect fourths in the Anastenaria folio notebook, as does as a melodic draft considering the possibility of interval multiplications. Xenakis was aware of the potential transformations which are implicit in these kinds of pitch manipulations. The change of modular bases for metabolae of sieves belongs to the same kind of operations conceptually speaking, as the operation remaps the intervallic distances of the underlying elemental congruences. For example, the metabola \(11_1\) of \(13_1\) transforms minor ninths into major sevenths. In this regard, the kinds of metabolae which have been shown in this article induce a complete remap of pitches—and pitch classes when coprime numbers are involved. In particular, the presence of coprime numbers enhances the variety of remapped pitches.
[6.10] Interestingly, some of the points above, in particular the second and the fourth, in essence connect Xenakis’ concerns around intervallic abstractions to some of Berg’s twelve-tone techniques. Berg was regarded by the Darmstadt serial composers as the least representative model of the core “trinity” of Second Viennese School. They viewed Webern’s works as most worthy of emulation and, to a lesser extent, Schoenberg’s.
[6.11] Unfortunately, Xenakis is no longer with us, and it is impossible to know if he would have first, agreed with the parallelisms I have stressed and second, publicly acknowledged them. In any case, from my current viewpoint, it is possible to sense some irony in rereading his first essay devoted to algebraic concerns of musical composition—the one presenting technical features of Herma. He suggested in the very opening paragraphs of the article that, for a proper exposition of his ideas, “we shall begin by imagining that we are suffering from a sudden amnesia” with regard to our previous musical knowledge (Xenakis 1992, 155).
Afterthought: The serial label
[7.1] Even if Xenakis were to have agreed with all or part of my final argument, I remain sure that he still would have raised a fundamental objection. As stated above, his algebraic reasonings ran in parallel with his original reflections upon in-time and outside-time structures in music. This aspect was taken up in his first text about sieves, in which he compared theoretical features of modal and serial music:
Traditional modes are partially outside-time, the relationships or logical operations imposed to sound classes, intervals, characters. . . are also outside-time. Since the discourse incorporates the before and the after, we are in-time. The serial order is in-time, a traditional melody too (Xenakis 1965, 33).
[7.2] The way Xenakis exploited his sieves was quite diverse. One could take for instance the case of Mists. In the opening measures, the ascending order of the main pitch sieve unfolds several times in polyrhythmic canons; by contrast, the central section of the score presents the sieve pitches in a cloud-like distribution from which it is not possible to infer any order or hierarchy. In the first case, the order of the sieve is aurally accessible to the listener in terms of register, but in the second case, this order is blurred by a mechanism of pitch selection which depends on stochastic laws (Squibbs 2002, 98–100). Xenakis’s sieves are deterministic, in this case for obtaining a particular pitch distribution. By contrast, the two different ways of temporally presenting the sieve pitches in this piano piece respectively depend on determinacy and indeterminacy, illustrating how Xenakis fully conceived his sieves as outside-time structures.
[7.3] I believe that the arguments provided in the previous section well support my main hypothesis, that Xenakis’ experience with twelve-tone music may have played a decisive role in his journey towards reconsidering some deterministic strategies for composition, in particular the case of pitch sieves. I further hope that the reader has noticed how, in light of Babbitt’s definition under paragraph [2.2] and Xenakis’ conception of outside-time structures, I have resisted treating the terms denoting twelve-tone techniques and serialism as interchangeable. Quite the contrary, I have often made use of the former as a way to neutralize the question of temporal order. All this leaves one issue to be settled, which is that the somewhat provocative question in the title of my article deserves a more nuanced answer. It is this: sieve theory should not be regarded as reminiscent of serial music, but as a consequence of some acquired knowledge of intervallic manipulations that Xenakis mastered by means of his speculations with twelve-tone techniques when he was younger—including the theoretical digressions beyond twelve-tone rows (cf. [4.10-12]). In other words, I believe that Xenakis was able to detect and isolate some deterministic aspects of intervals in the context of serial techniques that were meaningful to him as a composer, but was also willing to leave aside the intrinsic in-time features he was critical of. Many of these deterministic interval features neatly reappeared, unconsciously perhaps, in his latter formulation of sieve theory for pitches.
[7.4] Labels for compositional trends are often problematic, whether the involved composers accept them or not. The case of Boulez, who stood as the most belligerent champion of European total serialism, may illustrate this concern. His attitude famously crystallized in his harsh word of the term “inutile” (useless) leveled against non-serial colleagues (Boulez 1966, 149). His Structures I (1951–52) is a paradigmatic example of total serialism, but he rapidly pushed forward with the composition of Le Marteau sans maître (1952–55). This later piece was the first in which he exploited his harmonic multiplication. A twelve-tone row is split into several blocks, not necessarily homogeneous in size, and each block is projected, by transposing its interval content, onto the others in order to obtain different pitch-class reservoirs; here, serial order plays no substantial role (Boulez 1966, 168–69).(31) The procedure therefore is an abstract manipulation of the intervallic content of a twelve-tone row, which significantly blunts impact of its serial order. In this sense, Boulez’s multiplication also does not properly fit with the serial label against the backdrop of Babbitt’s definition. Even more important in the context of this article, it is not too far, conceptually speaking, from Xenakis’ algebraic speculations which led to the emergence of sieve theory. If Boulez had been aware of this, he could have been perhaps a bit more indulgent in his severe regard towards the musical approach of his Greek peer.
José L. Besada
Complutense University of Madrid
Edif. B
Calle del Prof. Aranguren, s/n
28040 Madrid
SPAIN
jlbesada@ucm.es
Works Cited
Agon, Carlos, Moreno Andreatta, Gérard Assayag, and Stéphan Schaub. 2004. “Formal Aspects of Iannis Xenakis’ ‘Symbolic Music’: A Computer-Aided Exploration of Compositional Processes.” Journal of New Music Research 33 (2): 145–59. https://doi.org/10.1080/0929821042000310621.
Babbitt, Milton. 1950. “Review of Polyphonie - Revue musicale trimestrielle; Quatrième cahier: Le Système dodécaphonique.” Journal of the American Musicological Society 3 (3): 264–67. https://doi.org/10.2307/829738.
—————. 1964. “Remarks on the Recent Stravinsky.” Perspectives of New Music 2 (2): 35–55. https://doi.org/10.2307/832481.
Bailey, Kathryn. 1992. “‘Work in Progress’: Analysing Nono’s Il canto sospeso.” Music Analysis 11 (2–3): 279–334. https://doi.org/10.2307/854029.
Barthel-Calvet, Anne-Sylvie. 2003. “MÉTASTASSIS-Analyse: Un texte inédit de Iannis Xenakis sur Metastasis.” Revue de Musicologie 89 (1): 129–87.
—————. 2011. “Xenakis et le sérialisme: l’apport d’une analyse génétique de Metastasis. Intersections 31 (2): 3–21. https://doi.org/10.7202/1013211ar.
—————. 2012. “L’archéologie d’un œuvre: analyse et présentation des carnets de jeunesse de Xenakis.” Revue de Musicologie 98 (1): 43–84.
—————. 2013. “The Messiaen-Xenakis Conjunction.” In Messiaen Perspectives 2: Techniques, Influence and Reception, ed. Christopher Dingle and Robert Fallon, 175–200. Ashgate.
Bauer-Mengelberg, Stefan, and Melvin Ferentz. 1965. “On Eleven-Interval Twelve-Tone Rows.” Perspectives of New Music 3 (2): 93–103. https://doi.org/10.2307/832507.
Besada, José L., Anne-Sylvie Barthel-Calvet, and Cristóbal Pagán Cánovas. 2021. “Gearing Time Toward Musical Creativity: Conceptual Integration and Material Anchoring in Xenakis’ Psappha.” Frontiers in Psychology 11:611316. https://doi.org/10.3389/fpsyg.2020.611316.
Boivin, Jean. 1995. La classe de Messiaen. Christian Bourgeois Éditeur.
Boulez, Pierre. 1966. Relevés d’apprenti. Editions du Seuil.
Carey, Norman, and David Clampitt. 1989. “Aspects of Well-Formed Scales.” Music Theory Spectrum 11 (2): 187–206. https://doi.org/10.2307/745935.
Chrisman, Richard. 1977. “Describing Structural Aspects of Pitch-Sets Using Successive-Interval Arrays.” Journal of Music Theory 21 (1): 1–28. https://doi.org/10.2307/843477.
Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35 (1–2): 93–173. https://doi.org/10.2307/843811.
DeLio, Thomas 1980. “Iannis Xenakis’ Nomos Alpha: The Dialectics of Structure and Materials.” Journal of Music Theory 24 (1): 63–95. https://doi.org/10.2307/843739.
Deliège, Celestin. 2003. Cinquante ans de modernité musicale: De Darmstadt à l’IRCAM. Contribution historiographique à une musicologie critique. Pierre Mardaga Éditeur.
Eimert, Herbert. 1950. Lehrbuch der Zölftontechnik. Breitkopf und Härtel.
Emmery, Laura. 2019. “Elliott Carter’s and Luigi Nono’s Analyses of Schoenberg’s Variations for Orchestra, op. 31: Divergent Approaches to Serialism.” Twentieth-Century Music 16 (2): 191–229. https://doi.org/10.1017/S1478572219000033.
Erwin, Max. 2020. Herbert Eimert and the Darmstadt School: The Consolidation of the Avant-Garde. Cambridge University Press. https://doi.org/10.1017/9781108891691.
Exarchos, Dimitris. 2007. Iannis Xenakis and Sieve Theory: An Analysis of the Late Music (1984–1993). PhD diss., Goldsmiths College.
—————. 2019. “The Berlin Sketches and Xenakis’s Middle-Period Style.” In Exploring Xenakis: Performance, Practice, Philosophy, ed. Alfia Nakipbekova, 21–36. Vernon Press.
Exarchos, Dimitris, and Yannis Stamos. 2008. “Iannis Xenakis’s Writing and Outside-Time Musical Structures.” 4th Conference on Interdisciplinary Musicology . http://cim08.web.auth.gr/cim08_papers/Exarchos-Stamos/Exarchos-Stamos.pdf.
Feneyrou, Laurent. 2002. Il canto sospeso de Luigi Nono: Musique et analyse. Michel de Maule.
Flint, Ellen R. 1993. “Metabolae, Arborescences and the Reconstruction of Time in Iannis Xenakis’s Psappha.” Contemporary Music Review 7 (2): 22–48. https://doi.org/10.1080/07494469300640131.
Gamer, Carlton. 1967. “Some Combinational Resources of Equal-Tempered Systems.” Journal of Music Theory 11 (1): 32–59. https://doi.org/10.2307/842948.
Gerhard, Roberto. 1952. “Tonality in Twelve-Tone Music.” The Score 6: 28–35.
Gibson, Benoît. 2002. “Theory of Groups: In Search of a Method to Analyze Group Structures in the Music of Xenakis.” Contemporary Music Review 21 (2–3): 53–66. https://doi.org/10.1080/07494460216655.
—————. 2019. “On Herma.” In Exploring Xenakis: Performance, Practice, Philosophy, ed. Alfia Nakipbekova, 21–36. Vernon Press.
Graebner, Eric. 1973. “An Analysis of Schoenberg’s Klavierstück op. 33a.” Perspectives of New Music 12 (1–2): 128–40. https://doi.org/10.2307/832274.
Hall, Patricia. 1985. “The Progress of a Method: Berg’s Tone Rows for Lulu.” The Musical Quarterly 71 (4): 500–19. https://doi.org/10.1093/mq/LXXI.4.500.
Harley, James. 2004. Xenakis: His Life in Music. Routledge. https://doi.org/10.4324/9780203342794.
Heinemann, Stephen. 1998. “Pitch-Class Set Multiplication in Theory and Practice.” Music Theory Spectrum 20 (1): 72–96. https://doi.org/10.2307/746157.
Iddon, Martin. 2013. New Music at Darmstadt: Nono, Stockhausen, Cage, and Boulez. Cambridge University Press. https://doi.org/10.1017/CBO9781139519571.
Jedrzejewski, Franck. 2008. “Generalized Diatonic Scales.” Journal of Mathematics and Music 2 (1): 21–36. https://doi.org/10.1080/17459730801995863.
Jones, Evan. 2001. “Residue-Class Sets in the Music of Iannis Xenakis: An Analytical Algorithm and a General Intervallic Expression.” Perspectives of New Music 39 (2): 229–61.
Kämper, Dietrich. 2004. “Olivier Messiaen und die musikalische Avantgarde der fünfziger Jahre: Zur Rezeption der Etüde Mode de valeurs et d’intensités.” In Kompositorische Stationen des 20. Jahrhunderts: Debussy, Webern, Messiaen, Boulez, Cage, Ligeti, Stockhausen, Höller, Bayle, ed. Christoph von Blumröder and Tobias Hünermann, 24–34. Lit Verlag.
Koblyakov, Lev. 1990. Pierre Boulez: A World of Harmony. Harwood Academic Publishers.
Krenek, Ernst. 1937. Über neue Musik: Sechs Vorlesungen zur Einführung in die theoretischen Grundlagen. Ringbuchhandlung.
Lefkowitz, David S. 1997. “Perspectives on Order, Disorder, Combinatoriality, and Tonality in Schoenberg’s Opus 33a and 33b Piano Pieces.” Intégral 11: 63–134.
Leibowitz, René. 1949. Introduction à la musique de douze sons: Les variations pour orchestre op. 31, d’Arnold Schoenberg. L’Arche.
Ligeti, György. 1958. “Pierre Boulez. Entscheidung und Automatik in der Structure 1a.” Die Reihe 4: 38–63.
Losada, C. Catherine. 2008. “Isography and Structure in the Music of Boulez.” Journal of Mathematics and Music 12 (3): 135–55. https://doi.org/10.1080/17459730802518318.
—————. 2014. “Complex Multiplication, Structure, and Process: Harmony and Form in Boulez’s Structures II.” Music Theory Spectrum 36 (1): 86–120. https://doi.org/10.1093/mts/mtu005.
Mâche, François-Bernard. 1988. “L’ellenismo di Xenakis.” In Xenakis, ed. Enzo Restagno, 77–92. Edizione di Torino.
Messiaen, Olivier. 1996. Traité de rythme, de couleur, et d’ornithologie, Tome III. Alphonse Leduc.
Meyer-Eppler, Werner. (1955) 1957. “Statistic and Psychologic Problems of Sound.” Die Reihe 1: 55–61. Originally published in German.
Montague, Eugene. 1995. “The Limits of Logic: Structure and Aesthetics in Xenakis’ Herma.” Ex Tempore 7 (2): 36–65.
Moore, Allan F. 1995. “Serialism and its Contradictions.” International Review of the Aesthetics and Sociology of Music 26 (1): 77–95. https://doi.org/10.2307/836966.
Morris, Robert. 1987. Composition with Pitch-Classes: A Theory of Compositional Design. Yale University Press. https://doi.org/10.2307/j.ctt1xp3ss4.
Morris, Robert, and Brian Alegant. 1988. “The Even Partitions in Twelve-Tone Music.” Music Theory Spectrum 10 (1): 74–101. https://doi.org/10.2307/745793.
Morris, Robert, and Daniel Starr. 1974. “The Structure of All-Interval Series.” Journal of Music Theory 18 (2): 364–89. https://doi.org/10.2307/843642.
Nielinger-Vakil, Carola. 2015. Luigi Nono: A Composer in Context. Cambridge University Press. https://doi.org/10.1017/CBO9780511842672.
Peck, Robert W. 2003. “Toward an Interpretation of Nomos alpha.” Perspectives of New Music 41 (1): 66–118.
Perle, George. 1964. “An Approach to Simultaneity in Twelve-Tone Music.” Perspectives of New Music 3 (1): 91–101. https://doi.org/10.2307/832239.
—————. 1977a. “Berg’s Master Array of the Interval Cycles.” The Musical Quarterly 63 (1): 1–30. https://doi.org/10.1093/mq/LXIII.1.1.
—————. 1977b. Twelve-Tone Tonality. University of California Press.
Piencikowski, Robert T. 1997. “Inschriften: Ligeti–Xenakis–Boulez.” Musiktheorie 12 (1): 7–16.
Santa, Matthew. 1999. “Defining Modular Transformations.” Music Theory Spectrum 21 (2): 200-229. https://doi.org/10.2307/745862.
Schaub, Stéphan. 2005. “Akrata, for 16 winds by Iannis Xenakis: Analyses.” In International Symposium Iannis Xenakis. Conference Proceedings, Athens, May 2005, ed. Anastasia Georgaki and Makis Solomos, 138–49. University of Athens.
Schoffman, Nachum. 1983. “Schoenberg Opus 33a Revisited.” Tempo 146: 31–42. https://doi.org/10.1017/S0040298200021161.
Shepard, Roger N. 1965. “Approximation to Uniform Gradients of Generalization by Monotone Transformations of Scale.” In Stimulus Generalization, ed. David I. Mostofsky, 94–110. Stanford University Press.
Slonimsky, Nicolas. (1947) 1975. Thesaurus of Scales and Melodic Patterns. Schirmer Books.
Solomos, Makis. 1997. “Esquisses pré-compositionnelles et œuvre: les cribles de Nomos Alpha.” Les Cahiers du CIREM 40–41: 141–55.
—————. 2002. “Xenakis’ Early Works: From ‘Bartókian project’ to ‘Abstraction’.” Contemporary Music Review 21 (2–3): 21–34. https://doi.org/10.1080/07494460216657.
—————. 2021. “Diagramme et pensée opératoire de l’espace chez Xenakis. La pluralité de la nature des graphiques compositionnels.” In Écrire comme composer. Le rôle des diagrammes, eds Franck Jedrzejewski, Carlos Lobo, and Antonia Soulez, 241–55. Éditions Delatour France.
Squibbs, Ronald. 2000. “Musical Composition as Applied Mathematics: Set Theory and Probability in Iannis Xenakis’s Herma.” In Bridges: Mathematical Connections in Art, Music, and Science. The 3rd Conference Proceedings 2000, ed. Reza Sarhangi, 141–52. Tarquin Publications.
—————. 2002: “Some Observations on Pitch, Texture, and Form in Xenakis’ Mists.” Contemporary Music Review 21 (2–3): 91–108. https://doi.org/10.1080/07494460216653.
—————. 2003: “Xenakis in Miniature: Style and Structure in à r. (Hommage a Ravel) for Piano (1987).” Perspectives of New Music 41 (1): 120–53.
Theureau, Jacques, and Nicolas Donin. 2006. “Comprendre une activité de composition musicale: les relations entre sujet, activité créatrice, environnement et conscience préréflexive”. In Sujets, Activités, Environnements. Approches transverses, ed. Jean-Marie Barbier and Marc Durand, 221–51. Presses Universitaires de France. https://doi.org/10.3917/puf.barbi.2006.01.0221.
Vandenbogaerde, Fernand. 1968. “Analyse de Nomos Alpha de I. Xénakis.” Mathématiques et Scences. Humaines 24: 35–50.
Varga, Bálint András. 1996. Conversations with Iannis Xenakis. Faber and Faber.
Vriend, Jan. 1981. “Nomos Alpha for Violoncello Solo (Xenakis 1966): Analysis and Comments.” Interface [currently Journal of New Music Research] 10 (1): 15–82. https://doi.org/10.1080/09298218108570328.
Wannamaker, Robert A. 2001. “Structure and Perception in Herma by Iannis Xenakis.” Music Theory Online 7 (3). https://mtosmt.org/issues/mto.01.7.3/mto.01.7.3.wannamaker.html.
Wyschnegradsky, Ivan. 1972. “L’ultrachromatisme et les espaces non octaviants.” La Revue Musicale 290–91: 73–130.
Xenakis, Iannis. 1955. “La crise de la musique sérielle.” Gravesaner Blätter 1: 2–4.
—————. 1956. “Wahrscheinlichkeitstheorie und Musik.” Gravesaner Blätter 6: 28–34.
—————. 1958. “Auf der Suche einer Stochastischen Musik/In search of a Stochastic Music.” Gravesaner Blätter 11–12: 98–111, 112–22.
—————. 1960–61. “Grundlagen einer stochastichen Musik/Elements of Stochastic Music Gravesaner Blätter” (delivered in four parts) a) 18: 61–83, 84–105; b) 19–20: 128–39, 140–50; c) 21: 102–11, 113–21; and d) 22: 131–43, 144–55.
—————. 1961. “La musique stochastique: éléments sur les procédés probabilistes de composition musicale.” Revue d’Esthétique 14 (4–5): 294–318.
—————. 1963. Musiques Formelles. Revue Musicale 253–54.
—————. 1965. “La voie de la recherche et de la question: formalisation et axiomatisation de la musique.” Preuves 177: 33–36.
—————. 1966. “Zu einer Philosophie der Musik/Towards a philosophy of music.” Gravesaner Blätter 29: 23–38, 39–52.
—————. 1967. “Vers une métamusique.” La Nef 29: 120–9.
—————. 1968. “Vers une philosophie de la musique.” Revue d’Esthétique 21 (2–4): 173–210. Modified version of Xenakis, 1966.
—————. (1988). “Sur le temps.” Revue de l’Université de Bruxelles 1–2: 193–200.
—————. 1990. “Sieves.” Perspectives of New Music 28 (1): 58–78. https://doi.org/10.2307/833343.
—————. 1992. Formalized Music: Thought and Mathematics in Composition. Rev. ed. Pendragon Press.
—————. (1955) 2001. “Problèmes de composition musicale grecque.” In Presences of / Présences de Iannis Xenakis, ed. Makis Solomos, 11–14. Originally published in Greek. Centre de Documentation de la Musique Contemporaine.
Zaplinty, Michael. 1975. “Conversation with Iannis Xenakis.” Perspectives of New Music 14(1): 86–103. https://doi.org/10.2307/832544.
Zervos, Georges. 2003. “Iannis Xenakis, les compositeurs de l’École de Vienne et le concept de structures hors-temps.” In Iannis Xenakis, Gérard Grisey. La métaphore lumineuse, ed. Makis Solomos, 213–24. L’Harmattan.
Footnotes
* This work has been funded by the research program “Atracción de Talento Investigador” (ref. 2019-T2/HUM-14477), financed by the Comunidad de Madrid. I warmly thank Mâkhi Xenakis for allowing me to reproduce some of his father’s compositional sketches.
Return to text
1. A rigorous presentation of this topic is found in Moore 1995. For a deeper reflection of its implications among the triad Boulez–Xenakis–Ligeti, see Piencikowski 1997.
Return to text
2. For any authorized translation by Xenakis, I henceforth refer to this anthology, which is the largest collection in English of his essays.
Return to text
3. Although Xenakis mainly developed his stochastic theories for composition during the late fifties and early sixties, the topic of determinism in his criticism of serial music emerged again in several technical interviews he gave in the seventies and beyond (Zaplinty 1975, 99; Varga 1996, 76–77). For a panorama and critique of Xenakis’ position with regard to twelve-tone music over time, see Zervos 2003.
Return to text
4. For any French article cited in this document, it is always my translation when a published one does not exist. This also applies to my forthcoming transcriptions of some passages of Xenakis’ sketches.
Return to text
5. The term neo-serialist applies to composers developing total serialism.
Return to text
6. Scholars’ analyses of Xenakis’ sieve theory and his approach to finite non-Abelian groups for composing are rarely interconnected. It is, however, important to remember that sieve theory, as I explain in [5.4-8], depends on modular arithmetic, which is structured by finite Abelian quotient groups from the integer one. In other words, Xenakis’ sieve theory should be considered as an intrinsic part of his exploitation of group theory.
Return to text
7. Xenakis also coined a third category, namely “temporel”, which he finally discarded but had an impact on the following dialectics for articulating the distinction between in-time and outside-time structures. For a comment upon these concepts, see Exarchos and Stamos 2008.
Return to text
8. Although this piece is usually dated 1953–54, there is evidence pointing to 1954 as the true date in which Xenakis started to compose it, see Barthel-Calvet 2011, 5.
Return to text
9. The Fibonacci series is also present in Metastaseis, see Barthel-Calvet 2003, 132–33.
Return to text
10. For a discussion about the impact of this score in the development of total serialism in Europe, see Kämper 2004; for a description by its author, see Messiaen 1996, 125–33. However, it is not possible to infer if Xenakis attended the classes related to Messiaen’s pieces form the documentation he has left (Barthel-Calvet 2013, 192).
Return to text
11. Xenakis was nevertheless far from fully grasping the main theoretical issues of even partitions in twelve-tone music, which were frontally tackled more than three decades later in America; see Morris and Alegant 1988.
Return to text
12. I assert this on the basis of several known dates, including when Messiaen analyzed twelve-tone music at his classes, a date written by Xenakis in further medium-size notebooks for the triptych Anastenaria (Barthel-Calvet 2012, 75–76), and the composition of Metastaseis.
Return to text
13. Also, there is no trustworthy evidence that Messiaen analyzed any of the mentioned pieces by Schoenberg to his pupils between 1951 and 1953 (Boivin 1995, 437–39).
Return to text
14. Beyond Messiaen, René Leibowitz was an influential teacher who championed twelve-tone music at that time in Paris (Deliège 2003, 43–54); sometimes both instructors even shared pupils. Xenakis never studied with Leibowitz but perhaps could have had access to information about Schoenberg’s mentioned pieces through his peers, or maybe by means of Leibowitz’s books. As a matter of fact, one of these books specifically focuses on Schoenberg’s Variationen für Orchester (Leibowitz 1949). It is not clear that he may have had recourse to them nonetheless.
Return to text
15. Before Babbitt (1950) coined the combinatorial terms, it is well known that Schoenberg systematically explored the semi-combinatorial properties of his rows in some of his works. For a comment on the impact of Schoenberg’s Variationen für Orchester op. 31 on other composers, see Emmery 2019; for analytical remarks upon his Klavierstück op. 33a, see Graebner 1973, Schoffman 1983, and Lefkowitz 1997.
Return to text
16. For some analytical remarks on this work, see Bailey 1992 and Feneyrou 2002.
Return to text
17. Nono found the twelve-tone row in the Italian edition of the book; see Nielinger-Vakil 2015, 36.
Return to text
18. A previous computational approach to this topic is found in Bauer-Mengelberg and Ferentz 1965.
Return to text
19. Berg also used a related method for transforming twelve-tone rows in his unfinished opera Lulu. The order for pitches are obtained by multiplying the ordinal position of its elements, modulo 12, by 5 or 7, see Hall 1985. This time, the analogy with standard twelve-tone techniques points toward retrograde rows, as number 11 can be regarded as its generator.
Return to text
20. Modular transformations are found in theoretical concepts by authors deeply influenced by twelve-tone music—take for instance the Perle-Lansky cycles (Perle 1964; 1977b)—but also in the work of composers which were far from this perspective—as happened for example with Béla Bartók. For a summary of the main literature on modular transformations during the twentieth century, see Santa 1999, 202.
Return to text
21. For further analytic comments upon Herma, see Montague 1995, Squibbs 2000, and Gibson 2019.
Return to text
22. The English version of his text about Herma incorporates a few extra lines in which he compared the relationships of the four main forms of a twelve-tone row with the algebraic properties of a Klein group (Xenakis 1992, 169–70).
Return to text
23. Nomos Alpha was not, however, the first work in which Xenakis exploited sieves for organizing pitches. Akrata (1964–65) predates it, although Xenakis did not problematize it through the publishing of a theoretical essay. For an analytical comment on this piece for wind instruments, see Schaub 2005. In addition, some resemblances of musical features in Herma and Nomos Alpha, in spite of their different algebraic perspectives, have been computationally modelized; see Agon et al. 2004.
Return to text
24. This choice is pivotal for my following argument, but it could be criticized as a denaturalization of Xenakis’ musical purposes when composing Nomos Alpha. As stated above, the composer considered a nonequal microtonal distribution of pitches. The choice of different partitions of the octave indeed modify the nature of the pitch sieve, but for a theoretical analysis of a variety and distribution of its disparate intervals, it is a minor issue to remap them onto a new equal temperament. The central matter is that Xenakis used modulo 18 for splitting the octave, and this numerical value shares prime factors with 12, namely 2 and 3. This property is the reason allowing to remap this mathematical sieve onto this particular pitch distribution, because the complex sieves conceived by the composer were always built on elemental sieves with bases 5, 7, 11, 13, and 17 (Xenakis 1992, 230–31). All these values are coprime with 2 and 3, therefore also with 12 and 18. Thus, features like non octave repetition are preserved because of this arithmetic property, which is more readable through the standard equal temperament remap.
Return to text
25. Xenakis also exploited his sieves for organizing rhythmic patterns, with his percussion piece Psappha (1975) as a paradigmatic example (Flint 1993; Harley 2004, 94–98; Besada, Barthel-Calvet, and Pagán Cánovas 2021), but this issue is outside the scope of my approach.
Return to text
26. The number in brackets points towards a compositional strategy Xenakis developed for rotating the intervals of the array, which entails reordering its values slightly.
Return to text
27. I consider here the notion of cyclical interval successions (Morris 1987, 40–41).
Return to text
28. This issue is equivalent to exploring the algebraic combinatorics of further equal-tempered partitions, a topic that, interestingly, appealed to scholars in America at the time Xenakis came with his sieve theory but independently, see Gamer 1967.
Return to text
29. Extensions of this concept related to further equal-tempered partitions have been developed in Clough and Douthett 1991 and Jedrzejewski 2008.
Return to text
30. It is intriguing again as to why he did not provide a simpler and more compact expression for this purpose, which is possible to be delivered. There is no particular reason for this choice in the accompanying text which would facilitate the understanding of Xenakis’ decision.
Return to text
31. For a scholarly analysis of this technique, see Koblyakov 1990, 3–33, Heinemann 1998, and Losada 2008 and 2014.
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
8993