Extending the Parallel Multiple-Analysis Processor: Perceived Meter in Post-Tonal Music*
James Sullivan
KEYWORDS: rhythm and meter, post-tonal music, non-isochronous meter, perceptual streaming, Danuta Mirka, Elliott Carter, Samuel Barber, Anton Webern
ABSTRACT: This article revisits the issue of perceived meter in rhythmically irregular post-tonal music by way of Danuta Mirka’s (2009) dynamic model of meter. Her model, which is a parallel multiple-analysis processor in the sense of Jackendoff (1991), accounts for rapidly fluctuating sensations of meter in the real-time listening process, while maintaining local regularity as a defining feature of metric processing. I offer two extensions to her model—one concerning the perceptual processing of non-isochronous meter and the other concerning meter in multiple perceptual streams—along with applications to music by Carter, Webern, Barber, Babbitt, Feldman, and Adès.
DOI: 10.30535/mto.29.1.4
Copyright © 2023 Society for Music Theory
If the concept of rhythm is highly problematic in tonal music, it would seem to be an almost prohibitively difficult subject in many twentieth-century compositions which abandon or at least make very ambiguous most of the staples of rhythmic analysis—meter, pulse, phrase, and cadence. That these compositions do not thereby become non-rhythmic already indicates the need to revise some of our notions about rhythm. A useful place to begin is to ask what is meter if this music can depart from it (in various degrees) yet still be rhythmic.
—Christopher Hasty (1981, 184–85)
Introduction
[1.1] Since Christopher Hasty’s early acknowledgement of the challenges associated with theorizing rhythm in post-tonal music, various methodologies have sought to account for this music’s rhythmic vitality as well as meter’s role in it. Some of these methodologies extend existing ones, while others are entirely new.(1) Some maintain established assumptions, while others rethink them.(2) Some implement analytical tools traditionally associated with rhythmic analysis, while others borrow tools from non-rhythmic domains.(3) Some treat rhythmic and metric features as the primary analytical object, while others integrate them with other parameters.(4) Some methodologies aim to handle post-tonal music specifically, or even the rhythmic practices of particular composers, while others are situated within broader theories of rhythm and meter that deal with tonal music.(5) And, of course, all of these methodological dichotomies intersect in various ways.(6)
[1.2] While many of these studies have clarified and deepened our understanding of rhythm and meter in post-tonal music, they have also brought to light further methodological questions and have, in some cases, entrenched methodological divides. Hence, for example, Gretchen Horlacher (1995) argues that Igor Stravinsky’s irregular motivic repetitions can produce shifts in perceived meter and then hypothesizes that meter might even be contextually defined “with respect to the internal motivic organization of the passage itself,” rather than “with respect to an implied external metrical grid” (302). This hypothesis then becomes fleshed out through Hasty’s (1997) processual approach to meter, which Horlacher (2001) adopts in a later article and explicitly contrasts with her earlier approach. Yet despite such apparent theoretical progress, aspects of this approach are far from universally accepted, as evidenced by Hasty’s (1999) exchange with Justin London (1999).
[1.3] The present study weighs in on a handful of methodological issues surrounding meter in post-tonal music by adapting and extending Danuta Mirka’s (2009) dynamic model of meter. Her model is a remarkable synthesis of various precedents, including Fred Lerdahl and Ray Jackendoff’s (1983) preference-rule theory, Jackendoff’s (1991) application of their theory to the real-time listening process, and Hasty’s (1997) theory of projection. Though originally designed for tonal music, Mirka’s model is especially well-suited to post-tonal music because of its ability to account for rapidly fluctuating sensations of meter in the real-time listening process while still maintaining local regularity as a defining feature of metric processing. The model accounts for perceptions that arise spontaneously, without reference to the notated barline, and usefully hypothesizes a lower threshold for perceived meter. This threshold enables a fine-grained distinction between musical surfaces that are at least somewhat metric (because they engage metric processing at least to some degree) and those that are truly ametric (because they persistently subvert one or more aspects of such processing).
[1.4] Applied in this way, Mirka’s model raises several methodological issues, including some that have always loomed over meter in post-tonal music and some that have arisen more recently. The former include the question of regularity and the role of the notated barline, while the latter include the issue of final-state versus real-time analysis and the role of active attending versus automatic perception. Ultimately, the strength of Mirka’s model will become clear through analytical application. However, its strength also lies in the way it manifests some early observations about rhythm and meter in post-tonal music, observations that engaged these very same methodological issues.
[1.5] I begin by working through some of these connections between Mirka’s work and her predecessors before moving on to an outline and an application of her model. I then present the first of two major extensions—a hypothesis for the perception of non-isochronous meters—after which I demonstrate how this extended model responds to various kinds of rhythmic irregularities that are broadly typical of post-tonal music. I then propose a second extension to Mirka’s model—a hypothesis for the perception of meter across multiple textural streams—along with an application. Finally, I return to non-isochrony and consider its perceptual limits both within and outside of post-tonal music. Doing so allows me to situate Mirka’s extended model within a broader cognitive landscape that includes categorical perception.
Motivating Mirka’s Model
[2.1] Though the structural role of notated meter in certain post-tonal compositions has been a fruitful subject for analytical discourse, its perceptual status has often been questioned.(7) Joel Lester’s (1986) reflections upon performing and listening to Milton Babbitt’s Composition for Four Instruments capture the basic problem. About a prior performance of the piece, he recalls:
Simply in order to play the right notes at the right time, I had to learn to hear my own part as well as all the other parts in the texture in a metric framework—the notated one. In effect, I had to memorize a silent click-track for the piece—a click-track against which the rhythms played out their jazzy syncopations and crossrhythms
. . . . I must have rather thoroughly memorized that metric grid, for if I listened to the concert tape not long after performing the piece, I could easily hear it automatically in the notated meter. . . But I can also remember well my surprise some months later when I listened again to the tape. In the interim, I had forgotten the measure-by-measure metric structure of the piece. And what had seemed to me in my days of familiarity a rhythmic-metric structure of crystalline clarity had become thoroughly opaque. Seemingly erratic impulses dominated the soundscape. Did an audience, any audience, hear only this latter piece and never the one that I had striven so hard to perform? (Lester 1986, 117)
[2.2] Ultimately, Lester concludes that the notated meter in Babbitt’s Composition and other similar pieces plays no role in our perception of certain rhythmic features, such as syncopation and duration, because the listener has no way of inferring the notated meter from the musical surface. He then opens the door for a perception-based theory of meter:
Attempts to explain or analyze the rhythmic-metric structure of this or much other posttonal music on the basis of these notations instead of on the basis of the perception of these values may very well be a misdirected study. I am not sure that I can contribute at this time to an approach to these issues that does not rely on assuming such a one-to-one relationship between notated symbol and perceived duration. But I am convinced that until we as theorists can create a model that solves this problem, we will have failed to systematically address temporal aspects of this music in a manner that accords with our hearing of the music. (Lester 1986, 126–27)
[2.3] The beginnings of the sort of model Lester suggests appear in David Lewin’s Generalized Musical Intervals and Transformations (1987). About the performance of Elliott Carter’s String Quartet no. 1, Lewin writes:
We have all heard and seen players fighting their way through slow lyrical lines, supposedly tranquillo like that of the first violin in measures 22–32 or sostenuto e cantabile like that of the cello in measures 27–32, all the while jerking their feet up and down spastically in an erratic approximation of some distantly related notational ‘beat.’ These lyric lines are not syncopated, as such a method of production makes them sound to both player and listener. Rather, each line has its own autonomous local time-unit [emphasis mine], with respect to which it should project an essentially “first-species” character. (1987, 70)
[2.4] While Lewin’s critique may be overstated in the context of chamber music—where, as Lester notes, coordination through the notated beat is often the only realistic option—Lewin’s observation that each line has its own “autonomous local time-unit” gets to the heart of Lester’s proposal. Namely, repeating durations within each individual line, and not the beats of the notated meter, project the passage’s “mensural character” (Lewin 1987, 62). While Lewin avoids the term “meter,” presumably to theorize mensuration and tempo as distinct from the notated meter, as well as to bypass contestable claims about perceived beat or metric hierarchy, his notion of autonomous local time-unit is nevertheless proto-metric, insofar as it carves out periodic regularities from perceived rhythmic cues. Lewin’s autonomous local time-unit is therefore a plausible foundation for a theory of perceived meter independent from the notated one.(8)
Example 1. Projection (after Mirka 2009)
(click to enlarge)
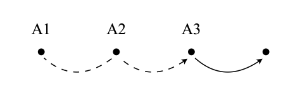
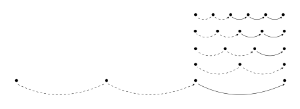
[2.5] Indeed, Lewin’s proposal is fundamentally similar to the notion of projection, which Mirka (2009) adapts from Hasty (1997) as the basic mechanism generating the metric structures described by Lerdahl and Jackendoff (1983). In Mirka’s adaptation, projection is schematized as in Example 1. Given two attacks on the musical surface (A1 and A2), the time interval between them (dotted arc) functions as a hypothesis (dotted arrow) for the location of a third attack. If that hypothesis is fulfilled (A3), then the projected timespan is confirmed. It becomes the basis for further projection (solid arrow) and generates beats or pulses (dots), terms I use interchangeably. If, on the other hand, the hypothesis is not fulfilled and a third attack does not occur at the anticipated moment, then the projection is denied. It does not become the basis for further projection and does not generate beats. Under this formulation, the presence of three regularly spaced attacks functions as the lower threshold for the perceptual formation of a level of beats.(9) The dots of Example 1 are not felt as beats until the moment in time when A3 confirms the projection. Hence, meter in its earliest stages arises retrospectively, even though projection is fundamentally prospective.
Example 2. Projection in Elliott Carter’s String Quartet no. 1, measures 22–26
(click to enlarge, see the rest, and listen)
[2.6] Example 2 gives a portion of the Carter passage discussed by Lewin. The annotations demonstrate that projection is a dynamic recasting of Lewin’s autonomous local time-units: each line’s time-unit is the timespan that the mechanism of projection hypothesizes and confirms. Furthermore, the notion that a given time-unit is projected autonomously, without reference to other time-units or to a common subdivision, is one of the compelling features of Mirka’s model—it is why the model so effectively accounts for fluctuating and competing sensations of meter in post-tonal music.(10)
[2.7] In addition to fulfilling Lester’s and Lewin’s calls for a perception-based theory of meter, Mirka’s model offers a nuanced solution to another perennial problem of meter in post-tonal music: regularity. Simply put, theorists disagree about the extent to which meter must be regular. Some require strict regularity, with irregularity arising at hypermetric levels through transformation rules (Lerdahl and Jackendoff 1983; Benjamin 1984). Others permit meter to be aperiodic if it satisfies certain well-formedness constraints that model repeating non-isochronous structures (London [2004] 2012) or if aperiodicity is driven by motive (Horlacher 1995). Still others allow meter to be more substantially irregular (Berry 1987; Kramer 1988; Leong 2011).(11) The disagreement is generally a matter of definition, which I have argued is better framed from a perceptual perspective: “are the various percepts associated with periodic meter, as well as the mental processes giving rise to them, the same as those associated with ostensible aperiodic metric structures?” (Sullivan 2021, 125). Finally, some treat regularity as repertoire-dependent (Lerdahl and Jackendoff 1983; Lerdahl 1992; Temperley 2001), a view supported by a handful of empirical studies that address meter perception and enculturation (Hannon and Trehub 2005a and 2005b; Hannon, Soley, and Ullal 2012).
Example 3. Projection and the pop-out effect in the opening of Carter’s String Quartet
(click to enlarge and listen)
[2.8] While I cannot hope to reconcile these competing positions, one piece of introspective evidence supports the idea that meter is constrained by regularity in some fashion. It is a phenomenon I call the pop-out effect, which David Temperley (2001, 301) has described as follows: “even when a piece has established a norm of being completely nonmetrical, we will immediately notice any suggestion of a beat or regular pulse.”(12) Example 3, which gives some of the prior context for Example 2, is instructive in this regard. The opening cello solo, while not entirely nonmetrical, is certainly metrically unstable. The sudden and sustained regularity of the second violin’s pizzicatos pops out of this context with a new pulse. The perception is immediate and seems to require no special effort on the part of the listener.(13) While Temperley adduces the pop-out effect as evidence that meter processing is always in operation and does not simply turn off in response to irregular metric cues, the pop-out effect also serves as evidence that meter perception is constrained by regularity in some way. If instead meter processing freely generated regular and irregular metric structures, then no pop-out effect would exist at all. The entire passage would be experienced as equally metric throughout. Thus, not only is meter processing always in operation, it must also always be seeking regularity.(14) Such “seeking” is well captured by the mechanism of projection. Irregular fluctuations and non-isochronous metric structures may very well arise in response to rhythmic irregularity—I will argue that certain ones do—but they must arise from a projective process that attempts to establish regularity in the first place. Thus, Mirka’s model offers something of a middle ground in the debate over regularity: meter must be regular at a local anticipative level, while the larger metric structures that arise from such anticipative regularity may be irregular.(15)
[2.9] This last point raises a distinction between meter as processed in real time versus meter as final-state analysis.(16) The two are often assumed to be subject to the same constraints, as when Lerdahl and Jackendoff (1983) develop well-formedness rules for the listener’s final-state understanding of meter and Jackendoff (1991) subsequently uses the same well-formedness rules to constrain the metric structures available to the listener at a moment-to-moment level. However, while real-time processing and final-state understanding are obviously related, I see no reason to assume outright that they are constrained in the same ways. My adaptation of Mirka’s model suggests that a final-state analysis can be irregular—sometimes substantially so—while the processing that leads to that structure demands greater regularity. Among other things, this distinction has important implications for the formalization of non-isochronous meters. It suggests that accounting for such structures is not just a matter of refining well-formedness constraints, as London ([2004] 2012) does. Rather it is also a matter of articulating how the listener might integrate the relevant irregularities into an anticipative projective process that is otherwise strictly regular.
[2.10] One final issue brought up by the pop-out effect is that of attention. The idea that perceptions can pop out without the listener’s intent to have those perceptions in the first place is consistent with the idea that music perception generally, and meter perception in particular, is modular.(17) Among other things, modularity holds that perceptual processing is reflex-like—fast, obligatory, domain-specific, and informationally encapsulated. For the real-time perception of meter, these principles mean that as a passage unfolds, the mind rapidly and automatically assigns it a metric structure (i.e., is fast and obligatory) based on (and only on) whatever metric cues the music currently presents (i.e., is domain-specific) without conscious effort on the part of the listener and independent of any “outside,” conscious knowledge about the passage (i.e., is informationally encapsulated). While modularity has been hotly debated since Jerry Fodor’s (1983) original outline (see, for instance, Barrett and Kurzban 2006), it nevertheless accounts for the pop-out effect and is a useful framework for thinking about meter perception. Furthermore, I would argue that we need not invoke all aspects of modularity—such as strict encapsulation—to adopt some of them—such as speed and obligatoriness. Indeed, without explicitly referring to modularity, London ([2004] 2012, 68) describes meter perception as “automatic and subliminal” while observing that trained musicians can “self-consciously reconstrue a rhythmic surface.” Thus meter processing for London is obligatory but not strictly encapsulated.
[2.11] Mirka (2009) explicitly adopts a modular view of projection, which sets her adaptation apart from Hasty’s (1997) original outline. For Hasty, projection in rhythmically irregular music is preconditioned by active attending. Reflecting on his analysis of Anton Webern’s Quartet, op. 22, he writes:
From the listener’s or the player’s point of view, it must be said that projective determinacy in the Quartet is often highly attenuated, and to feel the distinctions and contrasts I have suggested (or distinctions I have not suggested) will require a concentrated act of attention [emphasis mine]. If there is any lapse in attentiveness, this music may appear nonmetrical. But I believe that to the extent we do not perceive metrical distinctions, we will be deaf to a rhythm and a beauty Webern painstakingly sought to achieve. (275)
[2.12] By contrast, a modular approach to the same passage holds that any sudden presence of cues supporting projective regularity will be processed automatically and generate a local perception of meter. Such perceptions may be fleeting or rapidly changing, but they are still present because the mind cannot help but process the metric cues being presented. It is the manipulation of these sorts of reflex-like perceptions in much post-tonal music that, for me, imparts the kind of rhythm and beauty that Hasty finds in Webern’s Quartet.(18)
[2.13] To summarize, Mirka’s model fleshes out Lester’s and Lewin’s intuitions that meter must be rooted in the perception of local rhythmic regularities. Lewin’s autonomous local time-unit leads naturally to the notion of projection, which in turn operationalizes this study’s central premise: that final-state metric structures may be irregular but must arise from a real-time process that seeks moment-to-moment regularity. Finally, meter perception seems reflex-like and therefore exhibits features of modularity. The next section outlines these aspects of Mirka’s model in greater detail and demonstrates the model’s applicability to post-tonal music.
Projection and the Parallel Multiple-Analysis Processor
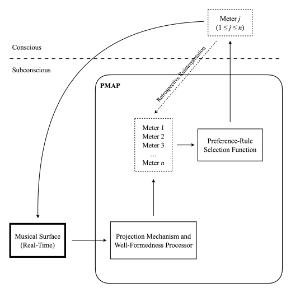
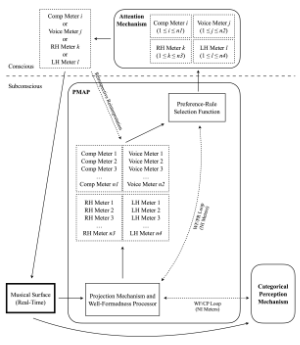
Example 4. Components and actions of the parallel multiple-analysis processor
(click to enlarge)
[3.1] Mirka’s model of meter, like Jackendoff’s (1991), is a parallel multiple-analysis processor (hereafter “a PMAP” or just “PMAP,” depending upon whether a general model or Mirka’s specific model is being referenced, respectively).(19) The fundamental feature of such a processor is that, as a passage unfolds, the processor simultaneously generates all well-formed analytical structures—in our case, metric structures—subject to certain constraints. In other words, the processor generates multiple analyses in parallel (hence “parallel multiple-analysis processor”). It does so automatically, and the analyses are subconscious at this stage of processing. When sufficient evidence, in the form of preference rules, supports one meter above the others, the processor’s selection function chooses that meter as the preferred one and surfaces it to consciousness. The chosen meter becomes the perceived meter and interprets musical events in the immediate past, present, and future. Non-preferred analyses are maintained subconsciously even if they do not surface. This enables retrospective reinterpretation (or retrospective reanalysis, to use Jackendoff’s word), whereby any well-formed alternative can supplant the surfaced meter if appropriately cued by phenomenal accents. Example 4 summarizes these basic theoretical components and actions.
[3.2] Jackendoff, and Mirka after him, select a PMAP among other alternative models because of retrospective reinterpretation. For a definite sense of meter to arise as a passage unfolds and for retrospective reinterpretation to be possible, meter processing must either (1) commit to a single metric structure and, when prompted to make a reinterpretation, backtrack to try out alternative meters in succession; or (2) generate all well-formed meters simultaneously and choose among them. The former is called a serial single-choice processor; the latter is a PMAP.(20) Jackendoff favors a PMAP in part because the serial single-choice model places high demands on processing speed: backtracking must keep up with the pace of the music. With a PMAP, the demands of processing speed are replaced with demands of processing space: multiple analyses must be computed simultaneously rather than successively. Jackendoff prefers a PMAP but acknowledges that the tradeoff is difficult to evaluate. Similarly, Temperley (2001, 209), whose computational model is also a PMAP, cautions against dismissing a serial single-choice model, since “it is possible, for example, that the system is backtracking, but is just doing it so quickly and effortlessly that we do not notice.” I follow Jackendoff and Mirka in adopting a PMAP as the most viable model.
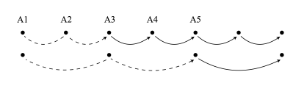
Example 5. Projection and metric hierarchy (after Mirka 2009)
(click to enlarge)
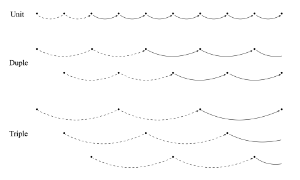
Example 6. Complete duple and triple projective hierarchies (after Mirka 2009)
(click to enlarge)
[3.3] In Mirka’s adaptation, PMAP generates meter through projection. In Example 1, projection generated a single level of beats. Metric hierarchy is generated by the simultaneous projection of nesting timespans. As shown in Example 5, an interval spanning the first and third attacks (A1 and A3) prompts a higher-level projection that itself is either confirmed or denied by a subsequent attack (A5). The confirmation of this larger projection (A5) functions as a lower threshold for what is traditionally thought of as meter. Given a musical surface that articulates one lower level of regularity, Example 6 shows all projections that could define a duple or triple metric hierarchy, with all phases shown. Because PMAP is a parallel multiple-analysis processor, these levels and phases are all elaborated subconsciously, and this is true every time PMAP encounters an isochronous series of attacks that functions as a unit level. It is up to the selection function to choose one nested hierarchy to surface to consciousness at a given time.(21)
[3.4] Thus outlined, PMAP makes a specific prediction about how we hear meter at beginnings of pieces. With respect to Example 5, PMAP predicts that, at the moments when A1 and A2 occur, we do not yet have a definite experience of pulse. After A3 occurs but before A5 occurs, we have a sense of pulse for everything up to the moment in question (assuming the selection function surfaces that beat level), but we do not yet have a definite sense of metric hierarchy. Only after A5 occurs do we have a definite sense of metric hierarchy (again assuming that the selection function surfaces that particular beat level). The process continues up the metric hierarchy, with each successively higher level confirmed one after the other and at proportionally wider and wider timespans. In this way, the perception of meter at the beginnings of pieces is always both retrospective and gradual.(22)
[3.5] Once a piece is underway and a metric hierarchy has been perceptually established, Mirka (2009, 22) supposes that the processor stops elaborating alternative metric structures until it is “woken up” by anti-metrical cues. This hypothesis results in two stages of meter, which she calls “finding meter” and “monitoring meter,” after London’s ([2004] 2012, 67–72) distinction between “finding the meter” and “keeping the meter going.” Temperley (2009, 310–11) critiques this hypothesis for a number of reasons, and I similarly do not adopt it.(23) Thus, in my formulation, PMAP is always in a state of meter finding. In the case of rhythmically irregular post-tonal music where meter constantly fluctuates, it often would be anyway. This assumption means that metric reinterpretation is swifter in my model than in Mirka’s. Instead of needing to “wake up” to restart the projective process and in turn overcome a series of three-attack thresholds, PMAP is already prepared to replace the surfaced meter with any projective hierarchy that has been subconsciously elaborated. The analytical consequence is that such later-surfaced hierarchies will sometimes appear immediately as solid arrows, whereas in Mirka’s model they might appear as a series of dotted arcs, dotted arrows, and solid arrows.
[3.6] There are several constraints on projection and the metric structures it produces. First and foremost are the attacks on the musical surface: until a projection has been confirmed, projection can only operate on actual attacks. As Mirka (2009, 25–27) notes, this assumption simplifies meter finding. In other models (Lerdahl and Jackendoff 1983; Jackendoff 1991), initially syncopated metrical analyses are well-formed possibilities that are typically discarded by the metrical preference rule (MPR) that attacks should coincide with strong beats (Lerdahl and Jackendoff’s MPR 3). Projection bypasses such analyses and treats this preference rule as the model’s fundamental generative rule.(24) Equally, any pair of attacks within certain temporal thresholds initiate a projection that has the potential to be confirmed. This obligatory processing conforms with Lerdahl and Jackendoff’s (1983) metrical well-formedness rule (MWFR) 1, whereby “every attack point must be associated with a beat at the smallest metrical level present at that point in the piece.” Recast in terms of projection, every attack point necessarily initiates a projective search for a second attack, which in turn has the potential to generate beats with a third attack.(25)
[3.7] Once confirmed, projections are maintained as long as there are attacks to sustain them. A confirmed projection can withstand some absent attacks but does not persist indefinitely without them. If the musical surface does consistently suppress such attacks, then the corresponding projection will vanish. This hypothesis explains our ability to sense a rest as metrically strong, while also observing that persistent rests of this kind undermine an established meter.(26) Neither Mirka nor I attempt to quantify the maximum number of absent attacks through which a confirmed projection can persist. Instead, I deal with the issue contextually.(27)
[3.8] Other constraints include a set of temporal limits on initial and larger projections and a set of well-formedness rules. Drawing from Hasty 1997 and London [2004] 2012, Mirka outlines a range of 0.2–2.0 seconds for initial projections (2009, 32–33) and an upper limit of 5–6 seconds for hypermeter (2021, 46), both of which I adopt. Under this rubric, A1 and A2 in Example 5 would need to be 0.2–2.0 seconds apart to induce projection, while A1 and A3 need only be less than 6 seconds apart to induce the larger projection. Were there no intervening A2, then A1 and A3 would need to be 0.2–2.0 seconds apart to induce the same projection. In this manner, smaller projections substantially facilitate the induction of larger projections with which they align.(28) Mirka also adopts a subset of Lerdahl and Jackendoff’s (1983) well-formedness rules, namely their MWFRs 2–4, dropping MWFR 1.(29) Ultimately, I will also drop MWFR 4 to accommodate non-isochronous meters and will recast MWFR 3 as a preference rule.(30) This leaves MWFR 2 as the only well-formedness rule not otherwise encompassed by projection or by my extensions to Mirka’s model.
[3.9] As PMAP subconsciously elaborates all well-formed projective structures subject to the constraints outlined above, the selection function continuously evaluates their compatibility with the musical surface and chooses one structure to surface to consciousness at a given time. It does so by way of preference rules. Despite some differences among authors, there is nevertheless broad consensus across the literature about the factors that influence meter perception and thereby constitute preference rules.(31) They typically include a variety of phenomenal accents, such as dynamic stress, durational stress, textural accentuation, melodic peaks, change of bass, and change of harmony, all of which prefer to be aligned with strong beats. They can also include non-musical cues like prosodic stress, as well as things like the preference for binary regularity, the preference to place strong beats early in a group, and the preference to interpret parallel groups with parallel metric structures.
[3.10] This last factor—melodic parallelism—is especially important in post-tonal music that lacks pervasive metric regularity. That is because melodic parallelism is known to facilitate the perception of meter (Temperley and Bartlette 2002). Mirka (2009) puts it well:
From the assumption that recognition of [melodic] parallelism is tantamount to recognizing patterns as having parallel metrical structure, it follows that the “false” meter is established as soon as the parallelism is recognized. This happens, at the latest, with the completion of the second segment in a given chain of repetitions. (138)
Here, Mirka is describing cases in which repeating motivic parallelisms generate a temporary false meter that is different from the established or notated one, but the same principle applies more generally to any case of melodic parallelism. Thus, in rhythmically irregular post-tonal environments, melodic parallelism can facilitate quicker and more rapidly fluctuating sensations of meter than might otherwise arise through the basic operations of PMAP. It can even create exceptions to the three-attack threshold, as will be seen later. Melodic parallelism therefore has privileged status among preference rules.
[3.11] Given the number of possible preference rules and the speculative nature of their interaction to produce perceived meter, I do not attempt to formalize their application in a rigorous manner. Indeed, such a formalization may be futile, since preference rules may be weighted differently by different listeners on different listening occasions.(32) Instead, I consider whatever rules seem most salient to me in each context, erring on the side of a minimal rather than all-inclusive list. Melodic parallelism and durational accent seem pervasively important in my hearing, though other factors like text stress arise as important in specific contexts. The role of harmony, which is an especially strong cue for meter in tonal music, is too complex an issue to explore here and deserves its own study.
[3.12] The basic operations and constraints outlined above, having principally to do with the configuration of attacks on the musical surface, make PMAP a compelling model of meter in post-tonal music. Projection maintains local regularity as a fundamental feature of meter processing, while the selection function allows different meters to surface in succession. Both are essential to account for the fleeting and fluctuating sensations of meter that characterize much post-tonal music. Additionally, while Examples 5 and 6 assumed a pervasive unit level in order to demonstrate parallel processing, such a level is not strictly necessary. All that is needed to induce projection and an accompanying sensation of meter are a few evenly and moderately spaced attacks within a short window of time. This is one of the benefits of PMAP as compared with many other models of meter and is in fact necessary if we are to account for perceived meter in, say, Example 3.
An Application of PMAP: Elliott Carter’s Long Melodies
Example 7. Projection in the opening of Elliott Carter’s Figment III for contrabass
(click to enlarge and listen)
[3.13] Example 7, which gives the introduction and opening melody of Elliott Carter’s Figment III for contrabass, demonstrates PMAP’s basic operations and constraints in a context with no audible unit pulse. The excerpt, as is typical of Carter’s long melodies, is built around changing durations that are multiples of a common but unarticulated notational unit. The melody is thus similar to that of the first violin in Example 2; however, the solo texture here offers a simpler context to evaluate PMAP as a model for perceived meter in post-tonal music.
[3.14] The excerpt begins with a short, rhapsodic introduction that opens up the instrument’s middle to low register. A long, lyrical line follows, beginning in the instrument’s upper register and ascending to the instrument’s extreme upper register, before plummeting to its lowest register. This melody moves in fluctuating rhythmic values, whose common notational unit is the triplet-eighth note. Rather than responding to this notational unit, my hearing seems to respond to the rhythmic patterning of the melody, latching on to whatever regularities exist in the patterning as the basis for meter.
[3.15] As measured in triplet-eighths, the melody’s rhythmic values are 7–5–4–4–8–4–5–5–4–4–6–4–5. Despite the overall irregularity, the pairing of 4s and 5s produces just enough regularity to prompt metric projections. Coming out of the introduction, the melody takes a moment to settle into a meter, speeding up its durations from 7 to 5 to 4. The irregularity of this opening segment
[3.16] Example 7 brings up several important issues, the first having to do with the three-attack threshold. While the long melody generates fluctuating sensations of pulse and a brief sense of metric hierarchy in coordination with its registral climax, PMAP predicts that the introduction generates a much weaker sense of pulse. As the annotations in the introduction show, note onsets are spaced such that they almost never confirm a projection proposed by two successive onsets. Only the initial five-eighth-note projection is confirmed, but even so, the passage’s third and fifth onsets seem to undermine its perceptual strength. The extent to which the listener senses pulse in the melody but not in the introduction provides evidence for the viability of the three-attack threshold.
[3.17] The second issue has to do with perceptual limits on projection itself. Example 7 assumes that PMAP can distinguish among quadruple, quintuple, sextuple, septuple, and octuple projections, even when the common unit is unarticulated. Yet that assumption should be questioned. In the absence of articulated subdivisions, how fine-grained can projective distinctions be? In Example 7, are the quadruple and quintuple rhythmic values registered as categorically distinct, in which case they generate conflicting sets of projections, or are they registered as categorically equivalent, in which case they generate and reinforce a single projective hierarchy? The answer determines the depth of metric hierarchy and the presence or absence of sensations like syncopation or metrical dissonance. If, as I have assumed, quadruple and quintuple projections are categorically distinct, then each change from one to the other supplants the established metric structure with a new one and generates indirect metrical dissonance. If, on the other hand, quadruple and quintuple projections are categorically equivalent, then each change from one to the other simply continues the established metric structure, generating a subtle push and pull of tempo rather than metrical dissonance. This hearing resonates with Lewin’s (1981) discussion of observations made by Jeanne Bamberger (1976) and conforms with John Roeder’s (2006) notion of “quasi-metric continuity.” Under Roeder’s model, the passage would be perceived as a series of shorts (4 and 5) leading into longs (8 and 6) at the registral extremes. The overall experience of directedness is similar in both hearings, though the perceptual particulars differ.(33) Which of these hearings holds also depends on performative details of absolute tempo and accentuation, in addition to the perceptual categories formed by the listener. I will return to the issue of categorical perception later.(34)
[3.18] A third issue has to do with performance. If the pulses generated by PMAP and thus inferred by the listener are those described above and not those of the notated meter, to what meter should the performer actively entrain? Recall that, in reference to similar melodic lines in Example 2, Lewin (1987, 70) argues in favor of entraining to a line’s “local time-unit,” rather than to a “distantly related notational beat.” In the language of PMAP, that means entraining to the shifting projections of Example 7. While such entrainment would prove difficult in the chamber setting of Carter’s String Quartet no. 1, where each line moves according to its own local time-unit within a larger polymetric configuration, such entrainment is much easier in the solo context of Figment III. For example, the bassist might initially entrain to the notated meter for the introduction, given no strong projective alternative, but then switch to counting the triplet subdivisions shown above the staff in Example 7, overtly feeling a 4-pulse on the
[3.19] But what if a performer or listener nonetheless chooses to entrain to the notated meter in Example 7? This brings up a fourth and final issue having to do with what might be termed passive versus active entrainment. In short, PMAP models passive entrainment, insofar as it aims to account for perceptions that arise automatically in a reflex-like manner. In principle, however, a performer or listener can entrain to whatever pulse they desire, with varying degrees of active effort depending on the context and the given pulse’s relationship to it. The attending sense of meter is present immediately, prior to any three-attack threshold. How does PMAP accommodate active entrainment? One possibility is suggested by John Paul Ito’s (2020) concept of focal impulse. To entrain to the notated beat, the performer—and I would argue the listener as well—matches focal impulses with the notated beat. Such active entrainment somehow overrides, interacts with, or functions as an input to passive entrainment. Exactly what this interaction might look like is too speculative to warrant extended discussion here. Instead, I simply suggest that focal impulses as a form of active entrainment should be kept in mind as a complicating factor when making introspective judgements about perceived meter.
Extending PMAP, Part 1: Non-Isochronous Meters
[4.1] Example 7 demonstrates the flexibility with which PMAP handles a rhythmically irregular surface by way of local regularity to produce a fluctuating sense of pulse and meter over the course of a passage. Moreover, the example demonstrates that a common rhythmic unit is not necessary to induce a sense of pulse and meter. This latter point suggests a more general one: while smaller projections facilitate larger projections with which they nest, they are not strictly necessary to induce those larger projections. Mirka (2009, 33–35) makes this point in an insightful analysis of the opening of Joseph Haydn’s String Quartet in D Major, op. 50, no. 6 (“The Frog”), where the largest metric level is established first and then gradually filled in by lower levels in coordination with harmonic resolution of an off-tonic opening. This aspect of the model invites a reconsideration of something not brought up by Mirka’s musical corpus—the status of non-isochronous meter.
Example 8. Divisions of an established projection
(click to enlarge)
[4.2] Consider Example 8 and suppose that some prior context has prompted PMAP to generate the larger projection shown. Then suppose that a later musical context prompts any one of the smaller nesting projections shown. Under traditional formalizations of meter, exemplified by Lerdahl and Jackendoff’s (1983) definition of metric well-formedness, all but the quintuple subdivision would be considered metric. Yet if the larger level has already been established through projection, as Mirka has shown to be a viable process in common-practice music, why would the sudden presence of a nesting, isochronous level that happens to include five beats instead of two, three, or four beats, suddenly negate the larger level’s metric status? Surely the presence of this new nesting pulse does not suddenly cause the established larger pulse to vanish. Indeed, all pairwise combinations of the larger level with one smaller nesting level pass Maury Yeston’s (1976, 66) definition of meter as, minimally, an interaction between two regular levels of motion, “a constant rate within a constant rate.”
Example 9. Projection in the opening of Anton Webern’s Piano Variations, op. 27, no. 3
(click to enlarge and listen)
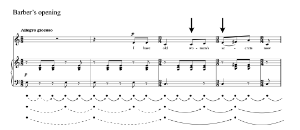
[4.3] The process suggested by Example 8 occurs at the beginning of Anton Webern’s op. 27, no. 3, shown in Example 9. The example gives Hasty’s (1981) segmentation of the passage into “units” or phrases, adjusted to associate rests with the notes preceding them. In my hearing of the passage, the largest projection crystallizes first with the onset of Unit 2, carving out the descending chromatic line
[4.4] At issue, then, is not the metric status of the outer isochronous levels but rather that of the intermediate non-isochronous level. Like London ([2004] 2012), I treat the ostensible metric sensations surrounding this level as properly metric in origin. Furthermore, I argue that the metric status of two outer levels stabilizes as metric the irregular patterning of an intermediate non-isochronous level. How, then, can we account for this level if projection is fundamentally regular?
Example 10. Projection and the problem of intermediate non-isochrony in the opening of Samuel Barber’s “The Secrets of the Old” from Four Songs, op. 13
(click to enlarge and listen)
Example 11. Hypothesis for PMAP and intermediate non-isochrony in the opening of Barber’s “The Secrets of the Old”
(click to enlarge and see the rest)
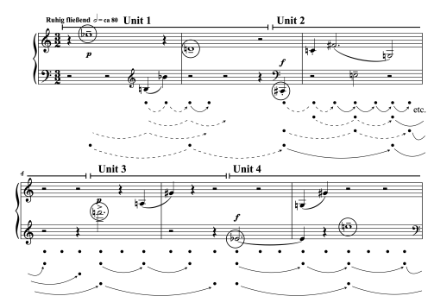
[4.5] Consider Example 10, which gives the piano introduction from Samuel Barber’s “The Secrets of the Old.” Here I readily perceive the notated
- Both outer levels are projected and eventually confirmed (marked with the rightmost arrow in Stage 1).
- There is a point in time after the larger timespan has been projected but before it has been confirmed that all duple and triple projections have already been confirmed (marked with the leftmost arrow in Stage 1).
- There is a point in time between (1) and (2) when PMAP recognizes, through preference rules, that no one established duple or triple level is as well-supported in its entirety as various components and combinations of multiple different duple and triple levels.
- One of those combinations is best-supported and nests with the larger level (circled in Stage 1).
- That best-supported combination surfaces to consciousness, or is made available for surfacing, in tandem with the larger level (Stage 2).(36)
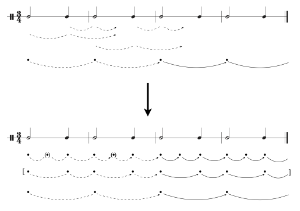
Thus hypothesized, the intermediate level effectively comes along for the ride, by way of the larger projection. This is represented visually in Stage 2 of Example 11, where the triple and duple timespans are measured together (dotted arcs) and then projected together (dotted arrows) in association with the quintuple level.(37)
Example 12. Projection of the intermediate level in isochronous versus non-isochronous meters
(click to enlarge)
Example 13. Projection and metrical dissonance in the opening of Barber’s “The Secrets of the Old”
(click to enlarge and listen)
Example 14. Projection and metrical dissonance in some hypothetical alternatives to Barber’s opening
(click to enlarge and listen)
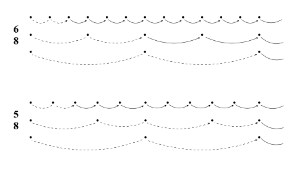
[4.6] If we accept the extension proposed in Example 11, then there is an important difference between PMAP’s handing of isochronous and non-isochronous meters. Because the intermediate level of a non-isochronous meter is tied to the larger level, it takes longer to surface than would an equivalent intermediate isochronous level. Example 12 demonstrates: the dotted-quarter pulse of
[4.7] This difference has important musical ramifications for “Secrets.” Example 13 places the song’s opening into its immediate context. After the
[4.8] Those who accept the possibility of non-isochronous meter but remain skeptical of the three-attack threshold will likely question whether it really takes so much time for a sense of meter to surface. For instance, in Example 13, might non-isochronous strong beats be heard wherever there is a bass onset, just as soon as the listener realizes that each bass onset initiates another “oom-pah” pattern? While a stock pattern like this can facilitate meter in a similar way as melodic parallelism, I question whether projective meter can surface quite so rapidly. Specifically, I question whether a proper sense of metric anticipation exists, to the extent that a listener expects the precise location of the next pulse at a given metric level, as opposed to perceiving an accent in the immediate past. I argue that such anticipation is the more important perceptual feature of meter, particularly since accent in the immediate past could conflate metric accent with phenomenal accent. For instance, at the onset of the third or even fourth eighth note in Example 13, do we really have a sense of duple or triple pulse above the eighth-note pulse to the extent that we expect another strong beat two or three eighth notes forward into the future? I do not think I do, and I suspect that is because the only cues for meter at this stage—duple bias and bass onset—are at odds. Furthermore, at the onset of the sixth or seventh eighth note, how could we anticipate the location of the next bass onset or strong beat when they have so far been spaced both two and three eighth notes apart? To my ear, only with the ninth and tenth eighth notes can I begin to anticipate the downbeat on the eleventh eighth note, and only because of the emergence of a larger five-eighth-note parallelism. Thus, while I acknowledge that melodic parallelism and stock patterns might facilitate perceived meter prior to the three-attack threshold (the eleventh eighth note), they do not entirely supplant that threshold.
[4.9] This discussion has pointed to several reasons why listeners might report hearing strong beats sooner than the three-attack threshold. I compile them below, along with several others:
Melodic parallelism—a type of intra-opus template matching, melodic parallelism has a facilitating effect on meter. The accompanimental pattern in Example 13 constitutes a melodic parallelism, albeit short and subject to contraction and expansion.
Schema, topic, and style—an instance of extra-opus template matching, the “oom-pah” pattern of Example 13 is highly stereotyped and may be sufficient to cue strong beats with each bass onset.(39)
Enculturation and metric archetypes—in addition to the top-down, extra-opus cues in (2), meters themselves can function as schematic templates. Those whose musical cultures commonly feature
rhythmic patterns may more readily impose a metric framework than those whose musical cultures do not.(40) Categorical perception—relatedly, those who have formed stable rhythmic categories for
rhythmic patterns may more readily impose a metric framework than those who have not. Categorical perception will be discussed in more detail later. Repeated listening—having heard Example 13 before, a listener might consciously or subconsciously impose
meter onto the passage prior to the point at which PMAP would have surfaced it in a first hearing. Embodiment, physical performance, and conscious intention—either listener or performer might intentionally hear or perform a passage with a particular meter from the outset, such as through focal impulses (Ito 2020). Furthermore, such intention may fall somewhere along a conscious-subconscious spectrum.
Introspection and notation—in attempting to account for one’s own hearing of meter, one might intentionally or unintentionally impose a particular metric hearing. A special case of this, which also intersects with (6), is when introspection occurs with score study, whereby a listener might intentionally or unintentionally impose a notated meter or pulse level.
Introspective misjudgment—in Example 13, even though the full non-isochronous metric hierarchy does not surface until the onset of measure 3 (or some slightly earlier moment due to the factors above), regular projections, whose timespans I have hypothesized form the basis of the hierarchy’s irregular level, are confirmed and could surface earlier. Such fleeting regularity could impart a false impression that the non-isochronous hierarchy has surfaced earlier than measure 3. Additionally, as already pointed out, introspection can easily conflate phenomenal accent with metric accent, particularly as concerns perception of accent in the immediate past.
Different ways of hearing meter—meter-related percepts range from relatively direct sensations, such as strong and weak beats, to relatively indirect sensations, such as the sense that text stress matches or mismatches its rhythmic setting. The numerous ways of hearing meter can be easily conflated in the process of introspection.
[4.10] Given the number of these factors and the extent to which they complicate introspection, it is no wonder that different listeners might offer competing claims about perceived meter, even in the stripped-down environment of Example 13. Yet meter perception being multi-faceted does not rule out the possibility of PMAP as a baseline meter processor. To the extent that PMAP does account for perceived meter in contexts with fewer complicating factors, such as Example 7, I argue that PMAP is still a viable working hypothesis for a baseline meter processor. Its interactions with other aspects of perceptual processing in turn makes for more precise and testable hypotheses about meter perception generally.(41)
[4.11] Having adapted PMAP to account for certain non-isochronous meters, we must drop the well-formedness rule that requires equally spaced beats at and above the level of the tactus (Lerdahl and Jackendoff 1983, MWFR 4). At this point, we might posit a new regularity rule that accommodates the local irregularity of Example 10, while still maintaining a degree of global regularity. London ([2004] 2012, 128–29) takes such an approach through a set of well-formedness constraints that accommodate certain non-isochronous structures. For reasons that will become clear in later examples, I will not follow suit. Instead, regularity continues to be captured by projection. Recasting regularity in this way means that PMAP still exhibits local projective regularity, even in contexts that lack global regularity.(42)
[4.12] As a final example for this section, let us return to the Webern passage in Example 9, whose quintuple meter can now be fully explained in terms of PMAP. Recall that the quintuple level crystallizes first at the onset of Unit 2, while the quarter-note level, which emerges in fits and starts, becomes established within Unit 2 and persists thereafter. As a result, half-note and dotted-half-note levels, which so far have only been initiated but not confirmed, begin to be elaborated and confirmed.(43) Yet my perception of these levels across Units 2 and 3 is at times fleeting and at other times vague, likely because these levels cut across the reigning quintuple projection and because phenomenal accents do not strongly support one of them over another.
[4.13] Unit 4 initiates a varied repetition of Units 1–3 as Units 4–6. Its rhythmic relationship to Unit 3 seems to reset the quintuple projection, which now carves out the ascending chromatic line
[4.14] Together, Examples 8 and 9 invite further reconsideration of metrical well-formedness. In particular, the idea that a large beat subdivided into fives is sufficiently metric (Example 8) and the intuition that such a metric structure can organize our listening experience for some time without a strong sense of an intermediate level (Units 1–3 of Example 9) together demand that we drop the well-formedness rule stipulating that beats must be organized hierarchically in twos and threes (Lerdahl and Jackendoff 1983, MWFR 3). Indeed, Lerdahl and Jackendoff (1983, 97) consider this possibility for certain musical idioms, in conjunction with dropping MWFR 4. And yet, the strong sense of 3+2 in Examples 10 and 13, combined with the intuition that an intermediate level eventually emerges in Example 9, suggest that there is still some cognitive pressure to construe meter with as rich a hierarchy as possible, be it isochronous or non-isochronous. Thus, I suggest that MWFR 3 is better conceived as a preference rule, which encourages rather than requires duple or triple hierarchies. While dropping MWFRs 3 and 4 allows for potentially objectionable non-isochronous levels within otherwise isochronous meters—such as a 2+1 level in
Applying PMAP
[5.1] With the proposed extension to PMAP in place, we are equipped to account for the moment-to-moment perception of meter in a wide variety of rhythmically irregular post-tonal music. I suggest that any such rhythmic context engages PMAP as outlined, prompting projections wherever there is sufficient local regularity. One useful way of parsing the rhythmic landscape of post-tonal music relative to the mechanisms of PMAP is through the extent and depth of rhythmic regularity. This approach leads to the following categories:
- music that features both a regular unit level and a regular organization of the unit level, which prompts PMAP to generate a single isochronous or non-isochronous meter throughout;
- music that features a regular unit level but fluctuating organization of the unit level (i.e., “mixed meter”), which prompts PMAP to generate a constant unit pulse and to surface larger pulses in potentially rapid succession based on the configuration of phenomenal accents;
- music that features fluctuating but well-articulated unit levels, which prompts PMAP to generate both unit and larger pulses in potentially rapid succession based on the configuration of attacks and phenomenal accents;
- music that lacks a unit level altogether but features larger fluctuating levels, which prompts PMAP to surface shallower hierarchies than those in (3); and
- music that lacks any sense of pulse whatsoever (i.e., “ametric music”), which consistently subverts one of the core components of PMAP’s projection mechanism.
While this classification is rough, porous, and non-exhaustive—an additional class of irregularity will be considered in the conclusion—it nevertheless represents many common post-tonal rhythmic structures and the ways they engage metric processing. (1) is relatively straightforward and exemplified by Example 10; (2) and (4) are exemplified by Examples 9 and 7, respectively; and examples of (3) and (5) will be discussed momentarily.
[5.2] I will not consider all five situations in detail here. Instead, I will consider one more example of (2), in order to give a more robust picture of that category; an example of (3), in order to glimpse how PMAP handles this very typical situation; and some examples of (5), in order to demonstrate precisely how music can be ametric. To that end, the mixed meter that follows Barber’s introductory excerpt in Example 10 offers a text-expressive use of (2), the metric modulations in the opening section of Elliott Carter’s “Canaries” offer a dynamic use of (3), and several passages by Milton Babbitt and Morton Feldman demonstrate the limited possibilities for (5).
Fluctuating Organization of the Unit Level: Mixed Meter in Samuel Barber’s “The Secrets of the Old”
Example 15. Projection and mixed meter in the opening of Barber’s “The Secrets of the Old”
(click to enlarge and listen)
[5.3] Example 15 gives the first full phrase of Barber’s “The Secrets of the Old.” While the two-measure introduction served as a testing ground for PMAP’s handling of non-isochronous meters, most of the song features mixed meter with a constantly articulated eighth-note pulse. Because the unit pulse is pervasively present, all larger projections that are integer multiples of the unit level are subconsciously confirmed shortly after the beginning and become available for rapid surfacing in response to changing phenomenal accentuation. Where the music stabilizes a particular notated meter for a short time, the corresponding projective hierarchy surfaces. Where the music avoids such local stability by mixing notated meters from measure to measure, only fluctuating duple and triple projections surface.
[5.4] As detailed already, I hear a complete
[5.5] The triple projection is short-lived, overwhelmed by the prosodic stresses and bass onsets of measure 6 and the beginning of measure 7. To my ear, these cues surface both a duple and, now more definitively, quadruple projection. With the more complete and sustained presence of
Fluctuating Unit Level: Metric Modulation in Elliott Carter’s “Canaries”
Example 16. Projection and metric modulation in the opening of Elliott Carter’s “Canaries” from Eight Pieces for Four Timpani
(click to enlarge, see the rest, and listen)
[5.6] The opening section of “Canaries” from Elliott Carter’s Eight Pieces for Four Timpani, given in Example 16, works through a series of metric modulations, each one altering the unit pulse by reconfiguring dynamic accents and motivic parallelisms to produce a local accelerando.(47) The first such switch occurs over measures 9–11. After the opening eight measures surface, suppress, and then resurface the notated
[5.7] The new
[5.8] Note that the non-isochronous projections in this passage are shown with solid arrows, because, under my formulation of PMAP, the larger quintuple, septuple, and nonuple projections have already been subconsciously confirmed. Were we to adopt Mirka’s two stages of meter—finding meter and monitoring meter—then the series of expansions would interact with the initial projective process in an especially dynamic way. Namely, the processor, which would have switched to monitoring
[5.9] The process of motivic-metric expansion across measures 15–18 is halted by measures 19–20, where dynamic accents draw out the quarter-note timespan of the previous non-isochronous
[5.10] Paradoxically, through a gradual accelerando across measures 1–25, the music arrives back at the same meter and tempo in which it began. The aural illusion—that each metric modulation takes us to a new faster tempo, even though we ultimately arrive back at the same starting tempo—is like the visual illusion of an M. C. Escher staircase and is a consequence of PMAP being drawn down carefully worked-out metric paths. Each metric modulation prompts PMAP to surface a new metric structure built from shorter and shorter projections, producing the passage’s sense of local accelerando. As projections shorten, higher-level projections move down into meter’s temporal sweet spot, and perception is gradually drawn up the metric hierarchy.(53) The metric relationships involved in each of the metric modulations are such that the highest levels of this process exhibit the same metric relationships as the metric levels at the opening.
Ameter: Milton Babbitt’s Serial Irregularities and Morton Feldman’s Wide Spacings
[5.11] Under PMAP, there are two ways in which music can be ametric: (1) note onsets can be spaced so irregularly that they subvert projective confirmation at every turn, or (2) note onsets can be spaced far enough apart that they do not induce projection in the first place. These two types of ameter are also described by Hasty (1997, 293). Both cases preclude a sense of meter by undermining PMAP’s projection mechanism.
Example 17. Unrealized projection in the opening clarinet solo from Milton Babbitt’s Composition for Four Instruments
(click to enlarge and listen)
Example 18. Realized projection in a rhythmic recomposition of Babbitt’s solo
(click to enlarge and listen)
[5.12] The first possibility—ameter as rhythmic irregularity or unrealized projection—requires a high degree of control over inter-onset intervals, since any two onsets within the relevant temporal thresholds mark out a timespan for projection. Returning to Example 1, in order to avoid projective confirmation, a third onset (A3) must not fall the same temporal distance from the second onset (A2) as the second does from the first (A1). This type of ameter was suggested by the introduction from Example 7, which avoids confirming all but the very first projection through a process of gradual rhythmic expansion beginning in measure 2. Example 17, which reproduces the opening clarinet solo from Milton Babbitt’s Composition for Four Instruments along with Lester’s (1986) rhythmic annotations, achieves the same type of ameter by serializing rhythm at two hierarchical levels with the pattern 1–4–3–2.(54) The patterning is such that for every pair of immediately successive onsets, there is no third onset to confirm a projection. The only larger regularities are the quintuple pairings of 1+4 and 3+2, but the corresponding projections never stabilize beyond a third attack because the unit level keeps changing. Furthermore, pitch- and rhythm-contour parallelisms, such as the opening’s low-high-low plus short-long composite contour (boxed), perceptually obscure both a serial segmentation and the quintuple projections. The passage truly sounds ametric.
[5.13] Yet not all serial treatments of rhythm are necessarily ametric. Example 18 recomposes Babbitt’s solo with the serial pattern 3–1–4–2. Here, a much stronger sense of meter arises, particularly at the end of the excerpt, due to the pattern’s internal rhythmic relationships and certain rhythmic relationships across segments. Namely, each serial segment confirms a quadruple projection, and the fourth segment continues and fills out the projection confirmed by the third segment. The perceptual result is one of meter gradually crystallizing, rather than one of meter systematically avoided.
Example 19. Un-initiated projection in the opening of Morton Feldman’s Piano and String Quartet
(click to enlarge and listen)
Example 20. Projection and the upper edge of entrainment in Feldman’s For Aaron Copland
(click to enlarge and listen)
Example 21. Metric blossoming in the opening viola solo from Feldman’s Rothko Chapel
(click to enlarge and listen)
[5.14] The second possibility for ameter—ameter as wide rhythmic spacing or uninitiated projection—appears frequently in Morton Feldman’s music. Example 19 gives the opening of Piano and String Quartet, which presents a series of slowly rolled chords in the piano, aligned with sustained chords in the strings. The careful alternation of
[5.15] PMAP’s activity increases in other sections of the Piano and String Quartet, where inter-onset intervals gradually move into the range of entrainment. Indeed, several of Feldman’s works seem explicitly concerned with exploring this upper threshold of entrainment. Tempo markings just over or under 60 are common and allow for easy control over the listener’s ability to infer meter. In such cases, inter-onset intervals that are more than twice as long as the marked tempo’s referential rhythmic unit fall outside of the range of initial entrainment, while shorter inter-onset intervals fall within that range. Example 20 gives the opening of For Aaron Copland, marked “quarter equals 56.” The solo violin’s inter-onset intervals hover around the half note, sometimes longer, sometimes shorter, thus riding the edge of metric entrainment. Such perceptual teasing is enhanced by the music's subtle but persistent irregularities. At one moment a brief sense of meter surfaces; at the next it is gone.(55)
[5.16] A more directed exploration of entrainment’s upper edge structures the opening viola solo of Rothko Chapel, given in Example 21. Marked “quarter equals 63–66 exactly,” the melody initially moves in slow rhythmic values beyond the threshold for entrainment, before gradually and somewhat indirectly transitioning into faster values within the range of entrainment. The melody metrically blossoms, gradually engaging PMAP from beginning to end.(56)
[5.17] The foregoing examples by Babbitt and Feldman suggest that meter, when formulated relative to PMAP’s constant search for local regularity, is quite pervasive in post-tonal music. While ameter is possible, it requires careful control over a composition’s rhythmic surface. Ameter is best thought of as a compositional technique employed in particular contexts—sometimes moment-to-moment contexts—rather than as a broad classification for styles, oeuvres, or even individual works.
Extending PMAP, Part 2: Perceptual Streaming and Multiple Meters
Example 22. Projection and multiple meters in the opening of Samuel Barber’s “At Saint Patrick’s Purgatory” from Hermit Songs
(click to enlarge and listen)
[6.1] So far, I have treated meter perception as singular, in the sense that PMAP’s selection function surfaces one meter at a given time for an entire musical texture. This has been an apt assumption for most of the examples so far, but it does not account for the full perceptual experience of passages that pit multiple competing meters directly against one another in different perceptual streams.(57) Example 22, which gives the opening of Samuel Barber’s Hermit Song “At Saint Patrick’s Purgatory,” is representative. The passage features three distinct textural layers, easily parsed as three distinct perceptual streams. Each layer supports a different meter—the piano’s left hand supports
[6.2] Multiple-meter perception is a subject of heavy debate.(58) Rather than enter the debate, I make a softer and hopefully less contestable observation: whether or not I can attend to all of the meters in Example 22 at a single moment, I can attend to each of the meters in turn by shifting my attentional focus to one or another part of the texture. As I make each attentional shift, the meter implied by the newly focused-on textural layer comes to the perceptual fore, at the expense of the meter implied by the previously focused-on textural layer. Allen Winold’s (1975, 209–211) comparison of this phenomenon with the well-known vase-face illusion is particularly apt.
[6.3] As I make each attentional shift, I hear the new meter retrospectively and prospectively interpreting both the individual layer that supports it and the texture as a whole. This phenomenon is analogous to retrospective reinterpretation, which was the initial basis for adopting a parallel multiple-analysis processor (Jackendoff 1991, 210–15). By the same line of reasoning, it follows that PMAP subconsciously elaborates all well-formed metrical structures for each individual perceptual stream, in addition to those elaborated for the composite texture. If not, then retrospective hearing of a particular stream’s meter after an attentional switch to that stream would not be possible. The selection function then evaluates a best-fit for each stream by way of preference rules and makes them available to consciousness. Then, one or another best fit surfaces to consciousness through selective attention.
Example 23. Multiple streams and the parallel multiple-analysis processor (Example 4 revisited)
(click to enlarge)
[6.4] Example 23 updates Example 4 to schematize the processing of multiple streams in Example 22. In this case, PMAP processes meter in three individual streams—voice, piano right hand (RH), and piano left hand (LH)—as well as meter in the composite (Comp) stream. The model readily generalizes to other multi-stream situations. (The categorical perception mechanism will be discussed in the conclusion.) Example 23 in turn gives a more precise way of framing the multiple-meters problem: once the selection function makes a best-fit for each stream available to consciousness, can it surface more than one of the best-fits simultaneously, with or without implicating selective attention? Again, I leave that issue open.
[6.5] Two potential objections to this model might be raised. First, how do we know that PMAP’s processing is structurally prior to selective attention? Perhaps selective attention restricts the information being processed by PMAP. By focusing on one textural layer, I might be forcing PMAP to process that layer at the expense of others. While plausible, this explanation fails to account for retrospective hearing after an attentional shift. If I am attending to the piano’s left hand in Example 22 and then shift my attention to the piano’s right hand, it would not be possible to hear
[6.6] The second potential objection has firmer footing: how do we know that PMAP is elaborating distinct meters for distinct streams, when the three meters in Example 22 would have been elaborated by PMAP anyway given the passage’s constant unit pulse? Perhaps PMAP is simply elaborating meters as usual and then surfacing one or another based on attentional focus. To answer this objection, another example is needed, specifically one that features competing meters across competing textural layers but that does not articulate a constant and common unit pulse. Recall that Example 2, like Example 22, features multiple textural layers, parsed as distinct perceptual streams. In Example 2, each stream supports its own “autonomous local time-unit,” which we reformulated as projective pulse. Unlike Example 22, there is no articulated unit pulse that is common to any pair of streams. Yet I experience a similar perceptual phenomenon surrounding meter and attentional shift as I do in Example 22. Thus, Lewin’s insights into Example 2, which prefigure essential elements of Mirka’s PMAP, also support my multiple-meter extension.
Conclusion: PMAP, Categorical Perception, and the Limits of Non-Isochrony
[7.1] I have sought to demonstrate that Mirka’s parallel multiple-analysis processor, properly extended, accounts for fluctuating sensations of meter in a wide range of rhythmically irregular post-tonal music and that these sensations arise from the model’s constant search for local regularity. Thus this model maintains moment-to-moment regularity as a fundamental feature of meter processing and thereby differs from others that drop Lerdahl and Jackendoff’s MWFR 4. As a final exploration of this model, let us return to the first extension, which incorporates non-isochronous meters into the model. There, I argued that an intermediate non-isochronous level was stabilized by isochronous outer levels. But what if a lower unit pulse had not been articulated? Is the larger level sufficient to stabilize the non-isochronous level as metric?
Example 24. Low-level non-isochrony in 16th- and 17th-century unequal triple meter (after Grant 2014)
(click to enlarge)
Example 25. Low-level non-isochrony in Mande drumming (after Polak and London 2014)
(click to enlarge)
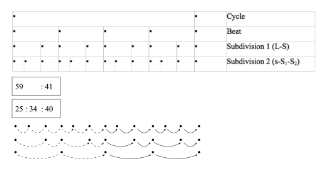
[7.2] This issue has been discussed in two musical contexts, widely divergent in time and place and both outside the musical scope of the present study. The first is the 16th- and 17th-century notion of unequal triple meter (Grant 2014, Chapter 3); the second is the practice of non-isochronous beat subdivision in African drumming (Polak 2010; Polak and London 2014). As historically conceived, triple meter differed from duple meter not in the number of beats each measure contains but in the length of beats. Specifically, triple meter consisted of two beats, with the first beat twice as long as the second. Example 24 reproduces a passage of unequal triple meter by Tielman Susato, which Roger Grant (2014, Example 3.4b) annotates with a metrical grid above the staff in the manner of Lerdahl and Jackendoff (1983). As Grant discusses, unequal triple meter violates modern definitions of metrical well-formedness, even though this conceptualization of triple meter was commonplace in 16th- and 17th-century theory and practice.
[7.3] Example 25 gives a beat hierarchy derived from Malian drumming by Rainer Polak and Justin London (2014, Figure 7.1a). Here, the cycle and beat levels are isochronous, but the two subdivisions are both non-isochronous. The pulses of Subdivision 1 approximate a 3:2 relationship, the longer of which can be subdivided as in Subdivision 2, such that pulses approximate a 1:2:2 pattern. In practice, the non-isochronous subdivisions from this repertoire are too fast to perceptually infer an isochronous lower level (Polak and London 2014, [92]). Furthermore, these approximations are merely that—approximations. In practice, performances stabilize much more complex relationships, such as those represented by boxed ratios in Example 25 (drawn from Polak and London 2014, Table 6.3). As Polak and London (2014, [107]) argue, such relationships “are not simply durational proportions—that is, expressively timed rhythmic groups—but are direct expressions of metrical structure,” which exemplify London’s ([2004] 2012, Chapter 10) “many meters hypothesis.”
[7.4] If Examples 24 and 25 truly describe metric experience, then they make two demands of PMAP. First, in addition to the non-isochrony that violates MWFR 4, Example 25 also demands that MWFR 3 be dropped, but for a different reason than Examples 8 and 9 suggest. Namely, the pattern’s final short operates as an indivisible beat appearing at two different levels of subdivision. Unlike the long, the beat does not divide into twos or threes, as MWFR 3 would require. Second, both Examples 24 and 25 stabilize a lowest non-isochronous level without the presence of an even lower isochronous level. This demands that we account for non-isochrony through a different mechanism than hypothesized in Example 11, since there is no lowest isochronous level to prompt the projections that might otherwise make up the non-isochronous level. Polak and London (2014, [117]) put it well: “The non-isochronous metric subdivisions of Ngòn and Bire challenge and enhance our understanding of metric well-formedness: one may have non-isochronous subdivisions yoked to an isochronous beat, just as one may have non-isochronous beats yoked to an isochronous layer of subdivision.”
[7.5] Given this observation, what is the mechanism by which a non-isochronous level can be “yoked” to a larger isochronous level? One hypothesis, suggested by Polak and London (2014, [99]), is categorical perception: if non-isochronous rhythms implicate stable rhythmic categories, then perhaps they can be stabilized as meter by a larger isochronous level alone.(60) My projective annotations in Examples 24 and 25 formulate this hypothesis in terms of PMAP.(61) Like in Example 11, the non-isochronous level surfaces in conjunction with the larger isochronous level. However, rather than resolving the issue of non-isochrony within the scope of PMAP—as in the process represented by Example 11 and subsumed by the well-formedness/preference-rule loop in Example 23—the present hypothesis resolves the issue by referring to an external categorical-perception mechanism, as shown Example 23. Whether or not this new well-formedness/categorical-perception loop replaces or merely supplements the well-formedness/preference-rule loop is unclear. Either way, incorporating categorical perception helps tease apart universality and enculturation. In Lerdahl and Jackendoff’s (1983, 99) model, the two overlap, since certain well-formedness rules are universal (MWFRs 1 and 2), while others involve acquired knowledge (MWFRs 3 and 4). In the present model, the two are cleanly separated: projection and well-formedness rules (MWFR 2) are universal, while preference rules and rhythmic categories are subject to enculturation.
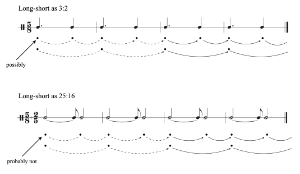
Example 26. Projection and categorical perception in 2:1 rhythmic patterns
(click to enlarge)
Example 27. Projection and categorical perception in some other long-short rhythmic patterns
(click to enlarge)
Example 28. Projection and categorical perception in the developmental retransition from Thomas Adès’s Piano Quintet
(click to enlarge and listen)
Example 29. Projection and categorical perception in the expositional second/third subject from Adès’s Piano Quintet
(click to enlarge and listen)
[7.6] Categorical perception also solves a problem with Mirka’s model that has not yet been addressed. Namely, in Example 26, a simple series of alternating halves and quarters will never surface a unit quarter-note pulse under the three-attack threshold. While this might not be a problem for historical approaches to unequal triple meter, it is a problem for Mirka’s modern approach to triple meter. Yet surely with just a few repetitions of the pattern, we deduce the unit pulse from the relationship between the long and short values. Because 2:1 is a stable rhythmic category, the present hypothesis proposes that we might deduce a quarter-note pulse once the larger pattern stabilizes a dotted-half-note pulse. This seems especially likely with a 2:1 relationship since the ostensible unit pulse is represented within the pattern itself. The similarity between Example 26 and Example 11 is striking—it suggests that a 2:1 pattern in
[7.7] If categorical perception, in tandem with PMAP’s projection mechanism, accounts for the non-isochronous meters in Examples 24 and 25, then we might ask whether the same mechanism extends to 20th- and 21st-century non-isochronous rhythms that lack an isochronous unit pulse. The removal of the eighth-note level from Example 10 is one such example and is shown in Example 27. If 3:2 is a stable rhythmic category, then a non-isochronous level might form through a similar process as that represented by Example 26. But do we also perceptually deduce the eighth-note unit, which is no longer part of the non-isochronous level as it was in Example 26? And what about the 25:16 pattern, which features an even more complex rhythmic relationship? While 25:16 resembles the complexity of stable rhythmic categories in African drumming, it seems doubtful that Western musicians and listeners, even afficionados of rhythmically complex 20th- and 21st-century music, will have experienced the degree of enculturation needed to stabilize such a rhythmic category. Thus, the pattern is likely normalized. But to what is it normalized? And if normalized, to what extent do we still perceive the rhythms as deviating qualitatively from their normalized paradigms? At this point, I can only propose that answers to these questions likely vary from listener to listener and that there is likely a limit to how fine-grained rhythmic categories can get. Whatever the answers, these examples probe the limits of rhythmic categorical perception and, as I am hypothesizing, the limits of a PMAP-based theory of non-isochronous meter.
[7.8] Lest the reader think that my last example is merely speculative, Example 28 gives a passage from the developmental retransition of Thomas Adès’s Piano Quintet. The passage is an extreme refraction of the one in Example 29, which is drawn from the piece’s exposition and is widely noted for its sudden calm amidst an otherwise tonally and rhythmically turbulent exposition.(62) The string parts in both passages, though complex in their rhythmic relationships with one another and with the piano, are internally regular and surface projective pulses along the lines suggested by my second extension to PMAP—that which incorporates multiple meters. The rhythmic relationships within the piano parts of Example 28 and 29 correspond to those of Example 27 (25:16) and 26 (2:1), respectively, and they pose the same issues within a larger multiple-meter context. I leave a full reconciliation of these issues with PMAP and categorical perception for another time.
James Sullivan
Michigan State University
402 Music Practice Building
East Lansing, MI 48824
sulli628@msu.edu
Works Cited
Bailey, Kathryn. 1991. The Twelve-Note Music of Anton Webern: Old Forms in a New Language. Cambridge University Press. https://doi.org/10.1017/CBO9780511552458.
Bamberger, Jeanne. 1976. “Cognitive Approaches to Music Composition and Perception.” Paper presented at First International Conference on Computer Music. Massachusetts Institute of Technology, October.
Barrett, H. Clark, and Robert Kurzban. 2006. “Modularity in Cognition: Framing the Debate.” Psychological Review 113 (3): 628–47. https://doi.org/10.1037/0033-295X.113.3.628.
Benjamin, William E. 1984. “A Theory of Musical Meter.” Music Perception 1 (4): 355–413. https://doi.org/10.2307/40285269.
Berry, Wallace. 1987. Structural Functions in Music. Dover.
Bregman, Albert S. 1990. Auditory Scene Analysis. MIT Press. https://doi.org/10.7551/mitpress/1486.001.0001.
Brower, Candace. 1993. “Memory and the Perception of Rhythm.” Music Theory Spectrum 15 (1): 19–35. https://doi.org/10.2307/745907.
Clarke, Eric. 1987. “Categorical Rhythm Perception: An Ecological Perspective.” In Action and Perception in Rhythm and Music, ed. A. Gabrielsson, 19–33. Royal Swedish Academy of Music.
Cohn, Richard. 1992. “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-Shifting Music.” Perspectives of New Music 30 (2): 146–77. https://doi.org/10.2307/3090631.
Cone, Edward T. 1960. “Analysis Today.” The Musical Quarterly 46 (2): 172–88. https://doi.org/10.1093/mq/XLVI.2.172.
Desain, Peter, and Henkjan Honing. 2003. “The Formation of Rhythmic Categories and Metric Priming.” Perception 32 (3): 341–65. https://doi.org/10.1068/p3370.
Fodor, Jerry A. 1983. The Modularity of Mind. MIT Press. https://doi.org/10.7551/mitpress/4737.001.0001.
Fox, Christopher. 2004. “Tempestuous Times: The Recent Music of Thomas Adès.” The Musical Times 145 (1888): 41–56. https://doi.org/10.2307/4149112.
Gallon, Emma. 2013. “Narrativities in the Music of Thomas Adès: The Piano Quintet and Brahms.” In Music and Narrative Since 1900, ed. Michael L. Klein and Nicholas Reyland, 216–33. Indiana University Press.
Grant, Roger Mathew. 2014. Beating Time and Measuring Music in the Early Modern Era. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199367283.001.0001.
Hannon, Erin E., Gaye Soley, and Sangeeta Ullal. 2012. “Familiarity Overrides Complexity in Rhythm Perception: A Cross-Cultural Study of American and Turkish Listeners.” Journal of Experimental Psychology 38 (3): 543–48. https://doi.org/10.1037/a0027225.
Hannon, Erin E., and Sandra E. Trehub. 2005a. “Metrical Categories in Infancy and Adulthood.” Psychological Science 16 (1): 48–55. https://doi.org/10.1111/j.0956-7976.2005.00779.x.
—————. 2005b. “Tuning in to Musical Rhythms: Infants Learn More Readily than Adults.” Proceedings of the National Academy of Sciences 102 (35): 12639–43. https://doi.org/10.1073/pnas.0504254102.
Hasty, Christopher. 1981. “Rhythm in Post-Tonal Music: Preliminary Questions of Duration and Motion.” Journal of Music Theory 25 (2): 183–216. https://doi.org/10.2307/843649.
—————. 1997. Meter as Rhythm. Oxford University Press.
—————. 1999. “Just in Time for More Dichotomies—A Hasty Response.” Music Theory Spectrum 21 (2): 275–93. https://doi.org/10.2307/745865.
Heyman, Barbara B. 2020. Samuel Barber: The Composer and His Music. 2nd ed. Oxford University Press. https://doi.org/10.1093/oso/9780190863739.001.0001.
Honing, Henkjan. 2013. “Structure and Interpretation of Rhythm in Music.” In The Psychology of Music, 3rd ed., ed. Diana Deutsch, 369–404. Academic Press. https://doi.org/10.1016/B978-0-12-381460-9.00009-2.
Hook, Julian L. 1998. “Rhythm in the Music of Messiaen: An Algebraic Study and an Application in the ‘Turangalîla Symphony.’” Music Theory Spectrum 20 (1): 97–120. https://doi.org/10.2307/746158.
Horlacher, Gretchen. 1995. “Metric Irregularity in ‘Les Noces’: The Problem of Periodicity.” Journal of Music Theory 39 (2): 285–309. https://doi.org/10.2307/843969.
—————. 2001. “Bartók’s ‘Change of Time’: Coming Unfixed.” Music Theory Online 7 (1). https://mtosmt.org/issues/mto.01.7.1/mto.01.7.1.horlacher.html.
Howland, Patricia. 2015. “Formal Structures in Post-Tonal Music.” Music Theory Spectrum 37 (1): 71–97. https://doi.org/10.1093/mts/mtv011.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press. https://doi.org/10.7551/mitpress/6575.001.0001.
Hyde, Martha M. 1984. “A Theory of Twelve-Tone Meter.” Music Theory Spectrum 6 (1): 14–51. https://doi.org/10.2307/745801.
Imbrie, Andrew. 1973. “‘Extra’ Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson, 45–66. W. W. Norton.
Ito, John Paul. 2020. Focal Impulse Theory: Musical Expression, Meter, and the Body. Indiana University Press. https://doi.org/10.2307/j.ctv1c3pdp3.
Jackendoff, Ray. 1987. Consciousness and the Computational Mind. MIT Press.
—————. 1991. “Musical Parsing and Musical Affect.” Music Perception 9 (2): 199–229. https://doi.org/10.2307/40285529.
Jones, James Rives. 1968. “Some Aspects of Rhythm and Meter in Webern’s Opus 27.” Perspectives of New Music 7 (1): 103–9. https://doi.org/10.2307/832428.
Kramer, Jonathan D. 1988. The Time of Music. Schirmer Books.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195116236.001.0001.
Larson, Steve. 2012. Musical Forces: Motion, Metaphor, and Meaning in Music. Indiana University Press.
Leong, Daphne. 2011. “Generalizing Syncopation: Contour, Duration, and Weight.” Theory and Practice 36: 111–50.
Lerdahl, Fred. 1992. “Cognitive Constraints on Compositional Systems.” Contemporary Music Review 6 (2): 97–121. https://doi.org/10.1080/07494469200640161.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Lester, Joel. 1986. “Notated and Heard Meter.” Perspectives of New Music 24 (2): 116–28. https://doi.org/10.2307/833216.
Lewin, David. 1981. “Some Investigations into Foreground Rhythmic and Metric Patterning.” In Music Theory: Special Topics, ed. Richmond Browne, 101–37. Academic Press.
—————. 1962. “Vocal Meter in Schoenberg’s Atonal Music.” In Theory Only 6 (4): 12–36.
—————. 1987. Generalized Music Intervals and Transformations. Yale University Press.
—————. 1993. “A Metrical Problem in Webern’s Op. 27.” Music Analysis 12 (3): 343–54. https://doi.org/10.2307/854149.
London, Justin. 1993. “Loud Rests and Other Strange Metric Phenomena (or, Meter as Heard).” Music Theory Online 0 (2). https://www.mtosmt.org/issues/mto.93.0.2/mto.93.0.2.london.html.
—————. 1999. “Hasty’s Dichotomy.” Music Theory Spectrum 21 (2): 260–74. https://doi.org/10.2307/745864.
—————. [2004] 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001.
Lopez, Gerardo. 2020. “Ambiguity and Meter in Copland’s Duo for Flute and Piano.” Paper presented at Indiana University Graduate Theory Association Symposium. Bloomington, IN, February.
Malin, Yonatan. 2006. “Metric Displacement Dissonance and Romantic Longing in German Lied.” Music Analysis 25 (3): 251–88. https://doi.org/10.1111/j.1468-2249.2006.00243.x.
—————. 2008. “Metric Analysis and the Metaphor of Energy: A Way into Selected Songs by Wolf and Schoenberg.” Music Theory Spectrum 30 (1): 61–87. /10.1525/mts.2008.30.1.61.
Marvin, Elizabeth West. 1991. “The Perception of Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varèse.” Music Theory Spectrum 13 (1): 61–78. https://doi.org/10.2307/745974.
Mead, Andrew. 1994. An Introduction to the Music of Milton Babbitt. Princeton University Press. https://doi.org/10.1515/9781400863334.
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791. Oxford University Press.
—————. 2021. Hypermetric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791. Oxford University Press. https://doi.org/10.1093/oso/9780197548905.001.0001.
Ohriner, Mitchell. 2016. “Attending to Free Rhythm.” Indiana Theory Review 32: 1–40. https://doi.org/10.2979/inditheorevi.32.2.01.
Polak, Rainer. 2010. “Rhythmic Feel as Meter: Non-Isochronous Beat Subdivisions in Jembe Music from Mali.” Music Theory Online 16 (4). https://doi.org/10.30535/mto.16.4.4.
Polak, Rainer, and Justin London. 2014. “Timing and Meter in Mande Drumming from Mali.” Music Theory Online 20 (1). https://doi.org/10.30535/mto.20.1.1.
Poudrier, Ève, and Bruno H. Repp. 2013. “Can Musicians Track Two Different Beats Simultaneously?” Music Perception 30 (4): 369–90. https://doi.org/10.1525/mp.2013.30.4.369.
Repp, Bruno. 2010. Review of Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791, by Danuta Mirka. Music Perception 28 (2): 201–4. https://doi.org/10.1525/mp.2010.28.2.201.
Roeder, John. 1994. “Interacting Pulse Streams in Schoenberg’s Atonal Polyphony.” Music Theory Spectrum 16 (2): 231–49. https://doi.org/10.2307/746035.
—————. 2001. “Pulse Streams and Problems of Grouping and Metrical Dissonance in Bartók’s ‘With Drums and Pipes.’” Music Theory Online 7 (1). https://mtosmt.org/issues/mto.01.7.1/mto.01.7.1.roeder.html.
—————. 2003. “Beat-Class Modulation in Steve Reich’s Music.” Music Theory Spectrum 25 (2): 275–304. https://doi.org/10.1525/mts.2003.25.2.275.
—————. 2004. “Rhythmic Process and Form in Bartók’s ‘Syncopation.’” College Music Symposium 44: 43–57.
—————. 2006. “Co-operating Continuities in the Music of Thomas Adès.” Music Analysis 25 (1–2): 121–54. https://doi.org/10.1111/j.1468-2249.2006.00235.x.
Rothstein, William. 1989. Phrase Rhythm in Tonal Music. Schirmer Books.
—————. 2011. “Metrical Theory and Verdi’s Midcentury Operas.” Dutch Journal of Music Theory 16 (2): 93–111.
Schulze, Hans-Henning. 1989. “Categorical Perception of Rhythmic Patterns.” Psychological Research 51: 10–15. https://doi.org/10.1007/BF00309270.
Service, Tom. 2012. Thomas Adès: Full of Noises, Conversations with Tom Service. Faber and Faber.
Stoecker, Philip. 2014. “Aligned Cycles in Thomas Adès’s Piano Quintet.” Music Analysis 33 (1): 32–64. https://doi.org/10.1111/musa.12019.
Sullivan, James. 2021. “Metric Manipulations in Post-Tonal Music.” Music Theory Spectrum 43 (1): 123–52. https://doi.org/10.1093/mts/mtaa020.
Taylor, Stephen Andrew. 2012. “Hemiola, Maximal Evenness, and Metric Ambiguity in Late Ligeti.” Contemporary Music Review 31 (2/3): 203–20. https://doi.org/10.1080/07494467.2012.717362.
Temperley, David. 1995. “Motivic Perception and Modularity.” Music Perception 13 (2): 141–69. https://doi.org/10.2307/40285692.
—————. 2001. The Cognition of Basic Musical Structures. MIT Press.
—————. 2008. “Hypermetrical Transitions.” Music Theory Spectrum 30 (2): 305–25. https://doi.org/10.1525/mts.2008.30.2.305.
—————. 2009. Review of Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791, by Danuta Mirka. Journal of Music Theory 53 (2): 305–28. https://doi.org/10.1215/00222909-2010-005.
—————. 2013. “Must Meter Be Regular?” Paper presented at Musical Metre in Comparative Perspective Conference, Cologne, Germany, April.
Temperley, David, and Christopher Bartlette. 2002. “Parallelism as a Factor in Metrical Analysis.” Music Perception 20 (2): 117–49. https://doi.org/10.1525/mp.2002.20.2.117.
Uno, Yayoi. 1996. “The Tempo-Span GIS as a Measure of Continuity in Elliott Carter’s ‘Eight Pieces for Four Timpani.’” Intégral 10: 53–91.
Unterecker, John. 1959. A Reader’s Guide to William Butler Yeats. Syracuse University Press.
Van den Toorn, Pieter C., and John McGinness. 2012. Stravinsky and the Russian Period: Sound and Legacy of a Musical Idiom. Cambridge University Press. https://doi.org/10.1017/CBO9781139108102.
Vendler, Helen. 2007. Our Secret Discipline: Yeats and Lyric Form. The Belknap Press of Harvard University Press. https://doi.org/10.2307/j.ctv1pncppz.
Westergaard, Peter. 1962. “Some Problems in Rhythmic Theory and Analysis.” Perspectives of New Music 1 (1): 180–91. https://doi.org/10.2307/832188.
—————. 1963. “Webern and ‘Total Organization’: An Analysis of the Second Movement of Piano Variations, Op. 27.” Perspectives of New Music 1 (2): 107–20. https://doi.org/10.2307/832108.
Winold, Allen. 1975. “Rhythm in Twentieth-Century Music.” In Aspects of Twentieth-Century Music, ed. Gary E. Wittlich, 208–69. Prentice-Hall.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. Yale University Press.
Discography
Discography
Adès, Thomas. 2005. Piano Quintet. Arditti Quartet and Thomas Adès. Recorded 4 July 2002. Adès Piano Quintet Schubert “Trout” Quintet. Warner Classics 5576642, compact disc.
Barber, Samuel. 1998. “The Secrets of the Old” op. 13, no. 2. Marilyn Horne and Martin Katz. I Will Breathe a Mountain: Songs of Barber, Bernstein & Bolcom. BMG; Sony Music 090266877126, compact disc.
—————. 29. Leontyne Price and Samuel Barber. Recorded 19 November 1954. Modern American Vocal Works: Premiere Recordings 1950–1953. Sony Classical MHK60899, compact disc.
Carter, Elliott. 2000. “Canaries” from Eight Pieces for Four Timpani. Daniel Druckman. The Music of Elliott Carter, v. 4. Bridge Records 9111, compact disc.
—————. 2008. String Quartet no. 1. Pacifica Quartet. Elliott Carter: String Quartets nos. 1 and 5. American Classics. Naxos 8.559362, compact disc.
—————. 2010. Figment III. Donald Palma. The Music of Elliott Carter, v. 8: 16 Compositions (2002–2009). Bridge Records 9314 A/B, compact disc.
Feldman, Morton. 1993. Piano and String Quartet. Kronos Quartet with Aki Takahashi. Recorded November 1991. Morton Feldman: Piano and String Quartet. Elektra Nonesuch 79320-2, compact disc.
—————. 2014. “For Aaron Copland.” Aisha Orazbayeva. Aisha Orazbayeva: The Hand Gallery. PRAH Recordings PRAH003CD, compact disc.
—————. 2015. Rothko Chapel. Kim Kashkashian, Sarah Rothenberg, Steven Schick, and Robert Simpson with the Houston Chamber Choir. Recorded February 2013. Rothko Chapel. ECM New Series 2378, compact disc.
Webern, Anton. 2001. Piano Variations op. 27. Maurizio Pollini. Maurizio Pollini Edition: Schoenberg: The Solo Piano Music, Piano Concerto; Webern: Variations op. 27. Deutsche Grammophon 471 361-2, compact disc.
Footnotes
* I would like to thank the reviewers for their many helpful suggestions during the submission process, as well as David Temperley, John Roeder, and Henry Klumpenhouwer for their feedback during earlier stages of writing. Thanks also to Joshua McNiven for assistance with engraving many of the examples and to my colleague Nick Schumacher for recording some of the audio.
Return to text
1. For example, Horlacher (1995) accounts for metric irregularity in Stravinsky’s music by adapting existing formulations of hypermetric irregularity to lower levels of the metric hierarchy—those existing approaches include Lerdahl and Jackendoff 1983, Benjamin 1984, Kramer 1988, and Rothstein 1989. By contrast, Roeder (1994) offers an entirely new pulse-stream methodology for Schoenberg’s music, later applying it to Bartók’s music (2001; 2004).
Return to text
2. Perhaps no study more dramatically rethinks established assumptions about meter than Hasty 1997, with well-worked applications to post-tonal music (see, in particular, Chapter 14). A useful comparison may be drawn with Lerdahl 1992, who approaches rhythmically complex post-tonal music with assumptions established in Lerdahl and Jackendoff 1983.
Return to text
3. Hence, Malin (2006) uses displacement dissonance as a tool to discuss Sehnsucht in Schoenberg’s “Unterm Schutz.” For adaptations of non-rhythmic tools to rhythmic ends, see Marvin’s (1991) application of contour theory to rhythm in Varèse’s music or Cohn’s (1992) and Roeder’s (2003) applications of set theory to rhythm in Reich’s music.
Return to text
4. For meter as primary analytical object, see Krebs’s (1999, Chapter 8) Ives and Schoenberg analyses. For metric processes as coordinated with pitch processes, see Roeder’s (2006) Adès study. For integration of rhythmic and non-rhythmic parameters within a broader analytical concept, see Malin’s (2008) energetic analyses of Schoenberg’s “Unterm Schutz” and “Valse de Chopin.”
Return to text
5. For some composer-specific studies, see Hyde’s (1984) study of pitch-metric relationships in Schoenberg’s twelve-tone music, Hook’s (1998) mathematical treatment of Messiaen’s rhythmic characters, or Taylor’s (2012) formalization of hemiolas and maximally even rhythms in Ligeti’s late music. For a broader treatment of rhythm and meter in post-tonal music, see Hasty 1981. For a theoretical treatment that thoroughly integrates tonal and post-tonal rhythm and meter, see Berry 1987—while the original 1976 publication predates Hasty 1981, the second publication nevertheless self-consciously intervenes in contemporaneous disciplinary investigations (see “preface to the dover edition”). For briefer treatments of post-tonal rhythm and meter within tonal-focused theories, see Lerdahl and Jackendoff 1983, Benjamin 1984, Temperley 2001, and Huron 2006.
Return to text
6. For instance, Hyde (1984) can be read as participating in all of the dichotomies, to the extent that her study: (1) extends Yeston’s (1976) methodology, while also introducing new concepts to replace certain tonal-oriented ones, (2) rethinks assumptions about Schoenberg’s ostensible abandonment of tonal rhythmic structures, (3) borrows traditional rhythmic tools from Yeston (1976), (4) integrates considerations of duration and pitch to articulate strata that interact with the notated meter, and (5) aims to account for the rhythmic practice of Schoenberg’s twelve-tone music, with broader implications for other twelve-tone music. Additionally, I should note that this survey cannot hope to be exhaustive. Other important sources in post-tonal rhythm and meter will be encountered throughout this essay, while still others have necessarily been omitted.
Return to text
7. In this regard, Webern’s Piano Variations, op. 27 has functioned as a veritable laboratory for investigating the distinct roles of notated and perceived meter. On the structural role of the notated
Return to text
8. For an exploration of sounding meter as distinct from notation that prefigures the present discussion, see Lewin 1962 on vocal meter in Schoenberg’s atonal music.
Return to text
9. For a critique of the three-attack threshold, see Temperley 2009, 310–11.
Return to text
10. Another model that Lewin’s conception of autonomous local time-unit anticipates is Roeder’s (1994) theory of pulse streams. Like local time-units arising from surface durations, pulse streams are “a series of successive, equal timespans, marked off by accented timepoints” (233–34) and are proto-metric (Roeder 2004, 46). As with projection, “every pulse must be consistent with actual attacks in the passage,” and pulse streams need not match the notated meter (Roeder 1994, 234). Just as local time-units or projections may fluctuate in coordination with surface durations, pulse streams come and go as rhythmic cues fluctuate. Two main differences between Roeder’s (1994; 2001; 2004) studies and mine are that his examples always feature a clearly articulated low-level pulse that is common to competing pulse streams, and his analytical application involves keeping track of individual pulse streams as defined entities that can be departed from and returned to. By contrast, my examples do not always feature a common low-level pulse (though some do), and my application of Mirka’s model focuses on the local perceptual effects of fluctuating projections, making no assumption that the listener keeps track of projections over long spans of time.
Return to text
11. For additional discussion of the debate, see Temperley 2013 and Ohriner 2016. The issue has also been framed in terms of conservative versus radical modes of listening, as originally distinguished by Imbrie (1973, 65). See Van den Toorn and McGinness 2012, Chapter 1 for an updated discussion.
Return to text
12. Temperley makes the same point about the perception of familiar harmonic structures in non-tonal music (2001, 303).
Return to text
13. A more regular meter crystallizes for the cello within the same vicinity and is also technically an instance of the pop-out effect. For me, the effect is more pronounced in the second violin, probably because the pizzicato timbre and dotted-eighth pulse are both new, whereas the cello’s quarter- and half-note pulses have already surfaced and dissipated in the opening solo.
Return to text
14. Jackendoff (1991, 218–19) similarly argues that meter perception, and perceptual processes in general, are always in operation.
Return to text
15. Among other things, this approach offers a more nuanced treatment of syncopation than generally exists for rhythmically irregular post-tonal music. On one end of the spectrum, Lerdahl and Jackendoff (1983, 97) model perceived meter in Stravinsky’s music by entirely dropping the assumption of regularity at and above the level of the tactus (MWFR 4). They argue that “strong beats will be heard wherever there are appropriate local details” and that this lack of regularity curtails the predictive framework necessary for syncopation. On the other end of the spectrum, Leong (2011) theorizes syncopation against a broad range of irregular metric structures, presumably all with equal salience. The present model instead suggests that syncopation is a local sensation resulting from a conflict between projection and incoming metric cues. To the extent that a series of syncopations could prompt a shift in projective meter, syncopation will also be isolated and brief.
Return to text
16. See Lerdahl and Jackendoff 1983, 3–4 for the broad distinction between “real-time” and “final-state.”
Return to text
17. See Fodor 1983 for the original outline of modularity. For applications to music, see Jackendoff 1987 and 1991 and Temperley 1995.
Return to text
18. It may be that Hasty and I are simply talking about different kinds of perceptions. A useful parallel may be drawn with Temperley’s (1995) discussion of motivic parallelism, wherein the automatic sensation of parallelism that arises from tonal transposition, for example, is categorically different from whatever sensation accrues to hearing, through sustained effort, that two series of pitches are retrograde transpositions of one another.
Return to text
19. The outline that follows presents the model’s main theoretical features. For a more detailed discussion, see Mirka 2009, 17–39 and Jackendoff 1991, 210–15.
Return to text
20. A third possibility that Jackendoff considers is a serial indeterministic processor, which is like the serial single-choice model, except that it delays making a definitive choice when confronted with indeterminacy. This model is rejected in part because it fails to account for a definite sense of meter as a passage initially unfolds.
Return to text
21. In analyses that follow, I generally will not show every subconsciously elaborated level. Instead, annotations will model whatever levels surface at a given moment, along with any strong alternatives that are relevant to the analytical discussion.
Return to text
22. Mirka (2021) describes a different process for hypermetric levels. Since I am mostly concerned with lower levels of the metric hierarchy, I rely primarily on her 2009 model.
Return to text
23. Temperley points out that: (1) there are situations in which an alternative meter surfaces simply because it is a better alternative and not because there is any particular challenge to the established meter; (2) if the model does not continue to elaborate alternatives, then it risks failing to account for an actual human perception; and (3) assuming that PMAP always generates alternatives is theoretically more parsimonious. In light of this critique, I see no obvious reason, other than the issue of cognitive load, to assume that PMAP ever stops elaborating well-formed alternatives. The problem of cognitive load is lessened if we assume a scrolling window of time within which retrospective reinterpretation can occur. In that case, and depending on the size of the scrolling window, the cognitive load required to maintain alternatives over the course of a piece would not be that much greater than the cognitive load required to generate alternatives at the beginning of a piece.
Return to text
24. There are cases in which an initially syncopated hearing seems desirable, such as Malin’s (2006 and 2008) energetic analyses of the opening of “Unterm Schutz.” PMAP’s generative rule would seem at odds with Malin’s analysis. However, as Malin (2008, 61) observes, “a listener who does not have a score and does not know the song hears only a regular pulse.” Only with a score and prior hearing of the passage will listeners “have supplied the missing pulse internally.” Thus, Malin’s observations actually support PMAP’s generative rule. The listener without score or prior knowledge of the song would have exactly the sort of fast, automatic, and reflex-like perceptions for which PMAP aims to account. Even the listener with score and prior knowledge has to put in effort to hear the passage as syncopated. The energetic tension that results could arise in part from a tension between the low-level operation of PMAP and some higher-level process by which the listener supplies the missing pulse.
Return to text
25. Mirka (2009, 15 and 25–27) similarly drops MWFR 1, reasoning that (1) it is of a different class than the other well-formedness rules, since it concerns the relationship between metrical structure and musical surface and not the nature of metrical structure itself, and (2) it unnecessarily forces a classification of extrametrical events, like grace notes, which seem not to induce beats. From a projective perspective, fast extrametrical events do not participate in projection if they fall below a certain temporal threshold, and they do not surface a metrical level if they do not satisfy the three-attack threshold. However, if ostensibly extrametrical events do in fact satisfy the basic conditions of projection, then they do generate beat levels through projection.
Return to text
26. On “loud rests” as a motivator for a dynamic model of meter, see London 1993. For a recontextualization of the same discussion within a more thoroughly developed theory of entrainment, see London [2004] 2012, 107–8.
Return to text
27. Repp (2010, 202) points to this as one of several open issues brought up by Mirka that music psychologists could fruitfully explore. Lopez (2020) puts forth an interesting hypothesis, whereby a projection might vanish with the same number of absent attacks as it takes for the projection to be confirmed initially.
Return to text
28. Mirka (2021, 46) qualifies the discussion with London’s ([2004] 2012, 27) observation that these temporal limits vary from person to person and with Brower’s (1993, 22) argument that the relevant memory thresholds are constrained not just by absolute time but also by the information contained therein. Thus Mirka, like Brower, concludes that the tonal phrase functions as hypermeter’s upper limit. Since the notion of post-tonal phrase is too complicated to address fully here, I fall back on the temporal thresholds outlined above, with the understanding that such thresholds may vary from listener to listener. I leave it to another study to tease apart the relationships between post-tonal phrase, memory, and (hyper)metric-temporal thresholds.
Return to text
29. These stipulate that: “every attack point must be associated with a beat at the smallest metrical level present at that point in the piece” (MWFR 1); “every beat at a given level must also be a beat at all smaller levels present at that point in the piece” (MWFR 2); “at each metrical level, strong beats are spaced either two or three beats apart” (MWFR 3); and “the tactus and immediately larger metrical levels must consist of beats equally spaced throughout the piece,” with beats of subtactus levels equally spaced between surrounding strong beats (MWFR 4).
Return to text
30. Temperley (2001, 35–37) similarly drops MWFRs 1 and 4, keeping only MWFRs 2 and 3.
Return to text
31. See, for instance, the commonalities among Lerdahl and Jackendoff 1983, 74–90, Temperley 2001, 30–39 and 48–51, and Mirka 2009, 39. For an example that differs in its preference rules, see Rothstein 2011.
Return to text
32. In turn, this means that listeners’ intuitions about each of the passages I consider may or may not align with my proposed hearing. In general, alternative hearings do not undermine the model, so long as differences can be accounted for in terms of preference rules. Such differences only contradict the model if they contradict the basic operations of PMAP. Throughout the analyses, I generally present just one hearing for expedience, though I do occasionally try to predict alternatives.
Return to text
33. Yet another possible hearing intersects with the conservative/radical dichotomy. Suppose that a listener does distinguish quadruple from quintuple pulses but, instead of radically switching between them, conservatively clings to the quadruple pulse as soon as it is clearly established. In that case, the melody will sound markedly syncopated from the
Return to text
34. Another complicating factor is performative micro-timing. I have assumed, and have offered as a recording, a relatively strict rhythmic performance of the passage. But many recordings of the piece are more flexible. How micro-timing intersects with the various possible hearings I have outlined above, as well as with the different approaches to performance that I outline below, is a complicated issue that deserves further study. One could imagine qualitative empirical work that interviews performers of this piece and seeks to interpret their conception of meter. One could in turn ask musicians to transcribe these recordings without prior knowledge of Carter’s notation. Would the interviews and transcriptions correspond in interesting ways? Would they correspond to any of the hearings I have suggested? Might they offer new ones? Would they confirm or contradict PMAP? Such a study could be fruitfully paired with a more quantitative experimental investigation of these matters, including of the three-attack threshold.
Return to text
35. My hearing is in line with that of Lewin (1987, 37–44), who observes a strong relationship between quarter-note time intervals 1 and 5 and pitch-class interval 11. Moreover, Lewin confirms the three-attack threshold when he argues that only after the onset of Unit 1’s D can we hear the quarter note “as a beat with which to measure other temporal intervals” (42).
Return to text
36. In this approach, well-formedness rules are not structurally prior to preference rules. In typical formulations of isochronous meter—including Example 4—well-formedness rules function like a filter, through which only well-formed combinations pass. Preference rules are then applied to determine a best fit among only the well-formed options. By contrast, here the two types of rules intermix, as the non-isochronous level is deduced in the first place through preference rules (see step 3). Hence, among other modifications to be discussed later, Example 23 will incorporate an additional two-way arrow between the initial processor and the selection function. The precise nature of this “well-formedness/preference-rule loop” will remain underdefined.
Return to text
37. The notion that non-isochronous levels “come along for the ride” sits well with London’s ([2004] 2012, 128–29) well-formedness conditions, which stipulate that non-isochronous levels can arise only in association with a larger isochronous level. Specifically, for inter-onset intervals (IOIs) on the N cycle to be non-isochronous, the beat cycle must be isochronous (WFC 4.1.1). For IOIs on the beat cycle to be non-isochronous, the IOIs on the N cycle must be isochronous (WFC 4.2.1). In addition, the cycle itself is assumed to be isochronous. In the case of Example 11, the N cycle corresponds to the eighth-note level and is isochronous, the beat cycle corresponds to the alternating triple and duple beats and is non-isochronous, and the full cycle corresponds to the quintuple level and is isochronous.
Return to text
38. If the reader does not find metrical dissonance an apt metaphor for this opening, then they will likely have trouble making this introspective comparison. Another way of introspectively evaluating my extension to PMAP through Example 14 is to ask, what is the principal pulse that you hear by the downbeat of “se-crets” in each case? My extension to PMAP predicts that the answers would be: regularly alternating triple and duple pulses in Barber’s actual opening, a duple pulse in the first hypothetical alternative, and a triple pulse in the second hypothetical alternative.
Return to text
39. On intra- and extra-opus template matching, see London [2004] 2012, 67–68 and Mirka 2021, 49. Both intra- and extra-opus templates have similar facilitating functions for meter, though their scopes and cognitive bases are different. Intra-opus templates are synthesized during a single listening experience and rely on both short-term working memory (in the case of immediate repetition) and long-term episodic memory (in the case of more distant repetition). Extra-opus templates are synthesized across numerous listening experiences, are an aspect of enculturation, and involve long-term semantic memory. On different types of memory and their relevance to meter, see Brower 1993.
Return to text
40. On schematic templates as top-down cues to meter, see Mirka 2021, 281. On meter perception as archetype matching, see London 1993. On enculturation and non-isochronous archetypes, see the Hannon et al. studies cited earlier (Hannon and Trehub 2005a and 2005b; Hannon, Soley, and Ullal 2012).
Return to text
41. The idea that PMAP is a baseline processor that interacts with other cues to meter is supported by Mirka’s (2021, 49) hypothesis that templates simply function as preference factors within a broader preference-rule system. It also sits well with London’s ([2004] 2012, 67–68) distinction between template matching and period extraction. While Mirka reads London as suggesting that either one or the other mode of attending is in operation at a given time, I read his discussion as suggesting that period extraction (i.e., the projective process) is always present but comes to the fore in situations that lack relevant templates. This reading of London supports a broader outlook—that post-tonal music often lacks such templates (melodic parallelism being an important exception) and therefore relies more exclusively on the projective process to impart meter.
Return to text
42. In this way, my approach also differs from that of other theorists who drop MWFR 4 but who offer no constraint in its place. See, for instance, Lerdahl and Jackendoff’s (1983, 97) brief account of meter in Stravinsky’s music (mentioned previously in the context of syncopation) and Kramer’s (1988, 98–108) account of hypermetric irregularity in tonal music.
Return to text
43. I show only those half- and dotted-half projections that lead toward a 3+2 organization of
Return to text
44. Note that these projections appear as solid rather than dotted arrows, as if beginning out of nowhere. As stated before, the reason is that all relevant levels have already been subconsciously confirmed. This brings up an important methodological point related to the use of projective arrows to represent perceived meter. Dotted versus solid arrows only represent a distinction in the subconscious stages of projection formation. They do not represent a distinction in conscious perception. For example, if a projection that is shown with dotted and solid arrows surfaces, such as the quintuple projection at the beginning of Example 9, then the argument is that the corresponding metric level is heard as structuring the beginning but in retrospect from whatever point the metric level actually surfaces. In this case, that point in time is as early as the onset of Unit 2 but not sooner. Additionally, the presence of a solid arrow does not necessarily indicate a surfaced level—it only indicates that that level is subconsciously confirmed and available for surfacing. Hence, multiple non-nesting solid arrows are shown with Unit 2, even though, in my hearing, only the quintuple level surfaces. It is entirely possible that another listener might hear this duple level momentarily replace the quintuplet level. Relatedly, the resetting of the quintuple level at the beginning of Unit 4, shown with solid arrows, does not necessarily indicate that the listener perceives
Return to text
45. Of course, there are a number of different ways that one might hear meter in this passage, particularly in light of the complicating factors mentioned previously. Even a PMAP-oriented hearing might surface an alternating 3+2/2+3 intermediate level across Units 4 and 5 or might surface various intermediate levels that cut across and dissipate the larger quintuple level, depending upon one’s weighting of preference rules and depending on rhythmic nuances in particular performances. I am simply pointing out that a non-isochronous
Return to text
46. My reading of Yeats’s poem differs from that of Barbara Heyman (2020, 231). She interprets the poem as an affirmation of “everlasting friendship among three aged women whose bond is perpetuated by sharing secrets of their youth.” Instead I take the speaker to be an old man who has at long last found answers (“secrets”) to questions of love that tormented him in his youth. My reading is more consistent with the rest of the poems in the ballad sequence “A Man Young and Old,” which explore contrasting experiences of love in a man’s youth and old age and that are sometimes taken to be autobiographical. See Vendler 2007, 122–26, and Unterecker 1959, 194–96.
Return to text
47. For an excellent and detailed analysis of the structural role of this movement’s metric modulations using the framework of a tempo-span GIS, see Uno 1996. I depart from Uno only in my basic view of meter. Uno argues that the movement, and Carter’s music after the late 1940s in general, is non-metric and instead plays with tempi through the interaction of timespans, marked off by metrically undifferentiated pulses. As will become clear over the course of my analysis, a PMAP-oriented view counters this assertion, instead arguing that: (1) such interplay of tempi is fundamentally metric, (2) our perception of meter and of timespans marked off by pulses are one and the same, and (3) such pulses are therefore metrically differentiated.
Return to text
48. While the unit dotted-quarter pulse in measures 1–8 is unequivocal, the larger dotted-half pulse is more ambiguous. I hear the one that aligns with the notated barline, but it is entirely possible that PMAP could surface a displaced dotted-half pulse for another listener.
Return to text
49. These projections are shown as beginning with solid arrows because they have already been confirmed in prior measures, though they were too weakly supported to surface there. That initial projective process is omitted for visual clarity.
Return to text
50. Even though the transition is gradual with respect to notation—accents support the upcoming meter, while notation expresses the prior meter—and with respect to metric cues—accents and some motivic parallelisms support the new unit pulse, while other motivic parallelisms support the previous unit pulse—the transition is not necessarily perceptually gradual, in that the perceptual flip from one to the other seems abrupt. This same distinction has been made by Temperley (2008) in the context of hypermeter, and it counters the traditional view that Carter’s metric modulations are necessarily gradual and seamless. What is perceptually gradual is the filling-out of new subdivisions across measures 7–8, where dotted eighths and dotted sixteenths are gradually introduced. Whether this process makes the larger metrical transition into measure 11 sound smooth or not is still debatable.
Return to text
51. Timbre, as determined by the location that the timpanist strikes the drum head, reinforces this hearing. The relevant instructions—C (center), N (normal), and R (rim)—are omitted from Example 16 for visual clarity but are present in the original score. Specifically, the timbral parallelism [N]–[C] aligns with the [3]–[2–2(–2)] rhythmic profile of both 7/8 and 9/8.
Return to text
52. Like measures 9–10, measures 15–18 are metrically transitional, in the sense that both passages mix cues of established and upcoming meters. However, to my ear, measures 15–18 more closely approximate a perceptual sense of transition, because their mixing of duple and triple timespans makes for a more ambiguous sense of tempo by mixing timespans that structure previous and upcoming tempi.
Return to text
53. See London [2004] 2012, Chapter 2 for a relevant discussion of temporal thresholds.
Return to text
54. For a contextualization of this rhythmic technique relative to Babbitt’s compositional practice broadly and this piece specifically, see Mead 1994, 38–45 and 55–76, respectively. For a discussion of the piece’s form in terms of integrated parametric structures, see Howland 2015.
Return to text
55. I take the notated half note as a strict metric ceiling in this example, though of course the exact upper limit will vary somewhat from listener to listener. With this metric ceiling, values equal to or shorter than the half note afford projection, while longer values do not. The resulting difference between absent projection (isolated dotted arcs), unconfirmed projection (dotted arrow), and confirmed projection (solid arrow) is particularly telling in this example. Each perceptual situation relates strongly to Feldman’s repeating rhythmic motives and manipulations.
Return to text
56. Since this example is slightly faster than the previous one, I take the notated dotted-half note as the metric ceiling. The main perceptual difference with a lower ceiling would be a less deep metric hierarchy at the end of the passage.
Return to text
57. On perceptual streaming, see Bregman 1990, as well as Temperley’s (2001, Chapter 4) preference-rule formalization.
Return to text
58. See, for instance, London [2004] 2012, Chapter 6, which argues against the idea; Temperley 2001, Sections 8.5 and 8.7, which is also suspicious of the idea but offers the standard hemiola as a possible exception; and Poudrier and Repp 2013, 370, which supposes that more complex rhythmic relationships facilitate multiple-meter perception because they prevent the listener from constructing composite beat patterns. With respect to the examples being considered, Temperley’s position suggests that multiple-meter perception might be possible in Example 22, whereas Poudrier and Repp’s position suggests that it is more likely in Example 2.
Return to text
59. This same argument is why Jackendoff (1991, 210–12) rejects a serial, single-choice model.
Return to text
60. For experimental studies on the categorical perception of rhythm, see Clarke 1987, Schulze 1989, and Desain and Honing 2003. For discussions of rhythmic categorical perception within broader discussions of rhythm and meter, see Huron 2006, Chapter 10; Honing 2013; and London [2004] 2012, Chapter 8.
Return to text
61. For demonstration purposes, these annotations artificially suppose that both examples constitute projective beginnings, even though Example 24 begins midway through a piece and Example 25 constitutes a metric grid established over time.
Return to text
62. Service (2012, 49) calls it an “A major island of stability,” and Fox (2004, 51) and Stoecker (2014) offer similar characterizations. Adès himself describes it as “a version of the second subject that becomes a third subject” (Service 2012, 50). See Gallon (2013, 223) for a similar formal reading.
Return to text
Copyright Statement
Copyright © 2023 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Fred Hosken, Editorial Assistant
Number of visits:
7040