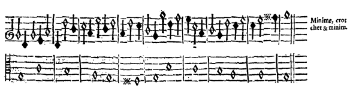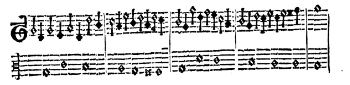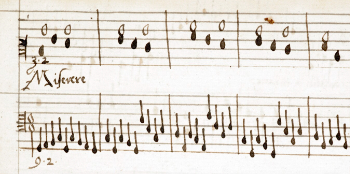Dispersed Meter in Elizabethan Polyphony*
Zoe Tall Weiss
KEYWORDS: History of theory, meter, mensuration, rhythm, performance, polyphony
ABSTRACT: Elizabethan untexted polyphony contains episodes of extreme rhythmic complexity, which suggest multiple and simultaneously conflicting metrical organizations between the individual parts, often without notated mensuration changes. Using techniques such as ternary regrouping (within a predominantly binary metrical environment) and displacement of ternary groups, composers were able to generate as many as four or five competing metrical realities among the different voices. These episodes of “dispersed meter” shed light on how metrical structures arise and function within Renaissance polyphony. They also offer an opportunity to take a more pluralistic view of metrical experience and the ways in which various views of meter can emerge within an ensemble performance. Focusing on the individual experience of meter from a first-person perspective, this article endeavors to align the analysis with the culture of partbook reading cultivated in Elizabethan England, pointing the way toward new theories of meter that center the perspectives of musicians rather than listeners.
DOI: 10.30535/mto.31.4.7
Copyright © 2025 Society for Music Theory
Fantasia
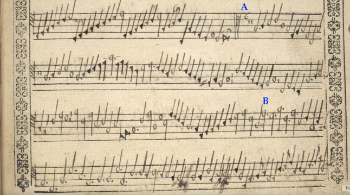
Example 1. Robert Parsons Ut re mi fa. Hamond Partbooks (tenor): GB-Lbl Add. MS 30482,
(click to enlarge)
[0.1] Say it is the late 1590s. You have been invited over by the Hamond family in Suffolk for an afternoon of domestic music making, and you are handed a well-loved partbook, the tenor. You may have an instrument to play, a viol perhaps, or maybe you plan to sing your part, regardless of whether or not the music has text. In the course of your music making with the Hamonds, you turn to folio 59v, a piece by Robert Parsons titled Ut re mi fa, shown in Example 1.(1) You recognize this text from your rudimentary musical training as a child as the first four syllables of the hexachord, and sure enough, as you and your three friends read the piece, you hear the cantus (the highest part) slowly sing the six pitches of the hard hexachord as a sort of cantus firmus, first up, then down: G, A, B, C, D, E, E, D, C, B, A, G.(2) This pattern repeats six times before all four parts arrive at a fermata and a section break (see point “A” in Example 1).
[0.2] The second section proceeds similarly to the first, but the rhythms have changed. In the first section, the hexachord was sung in breves (double whole notes) and you were tapping your toes to the semibreve (whole note) pulse.(3) Now, the hexachord is being sung as perfect semibreves (dotted whole notes), and you’re tapping your toes along with those perfect semibreves which your part subdivides into three minims (half notes). As you arrive at the point labeled “B” in Example 1, you encounter a new rhythmic pattern: dotted minims (dotted half notes) as well as groupings that add up to a dotted minim. Where you had previously been playing three minims per foot tap, you now play two dotted minims per foot tap. This is not hard to accomplish because your foot taps are aligned perfectly with the onsets of the cantus part’s hexachord pitches. Yet you and your friends have not ventured far into this passage before the music falls apart, and you are all forced to stop. The rhythm was a mess, and your two friends performing the altus and bassus parts are looking extremely confused. They both squint at their partbooks and see the following texts written at the beginning of the second part of the piece:
“If you c[a]nnot singe ye some p[ar]te let it a lonne” (GB-Lbl Add. MS 30481, f.64r, altus partbook)
“The seconde p[ar]te is good: but that it is so hard: I will not singe this p[ar]te” (GB- Lbl Add MS 30483, f.66v, bassus partbook)
Example 2. Robert Parsons Ut re mi fa. Hamond Partbooks (altus): GB-Lbl Add. MS 30481, f. 64r
(click to enlarge)
At this point, you, the tenor, might look over at your friend’s altus partbook (Example 2) and think, “why is she whining about how hard her part is? It merely switches to the same dotted minims as my part does, and I had no problem with it!”
[0.3] But during the group’s next attempt at the passage, you notice that your friend’s dotted minims are not aligned with yours, nor with the cantus firmus (the way yours are), but are instead delayed by a minim (half note) so that her foot tapping is offset from your own. As the four of you get the hang of the passage, you notice that the bassus part, too, has dotted minims, which are delayed from your own part by a semiminim (quarter note), and his foot tapping, remarkably, comes at a different time than anyone else’s. When you finally make it through the passage and lock back into a shared pulse, all four of you exhale audibly and sink back into a comfortable groove.
Introduction
Example 3. Robert Parsons Ut re mi fa, score of mm. 116–34 (Audio: Phantasm 2014).
(click to enlarge and listen)
[1.1] While fanciful, this description nonetheless captures something important about this extraordinary passage reproduced in score format in Example 3. The textual annotations quoted above indicate that some early modern players of this passage also recognized that it was difficult to play.(4) This passage in the Parsons, however, is not unique; others just as complex (and in similar ways) crop up in a dozen or so pieces from this era. In this article, I examine a small pocket of Elizabethan repertoire that cultivates transient episodes of rhythmic complexity— manipulating the surface rhythms of the music in ways that suggest multiple and simultaneously conflicting metrical organizations between the parts.
[1.2] Richard Cohn (2020, 210) defines meter as “an inclusionally related set of distinct, notionally isochronous time-point sets.” If we attempt to apply this definition to the four parts of the Parsons in this passage only, we find there are three simultaneous meters, identical in their organization but non-aligned. The top line, the cantus firmus, is a single isochronous time-point set whose subdivisions are only defined by the other parts. Melodic groupings of cantus firmus notes could certainly be construed as a higher-level pulse, though one slow enough to strain the boundaries of perception. The experience of playing or singing the cantus firmus is a deeply metrical one, but its sense of meter (in Cohn’s definition) relies on its relationship to the other parts. In measures 116 and 117 of the score in Example 3, the other parts subdivide the cantus firmus’s values into three (and further subdivide those three values in two). In measure 118 and following, the tenor provides a two-fold subdivision of the cantus firmus values (with a further subdivision of those values by three). The bassus and altus do likewise, but offset from the cantus firmus and tenor pair and from each other. These three unaligned meters continue in stable parallel for quite some time before the arrangement disintegrates and eventually returns to the original single meter: groups of three minims per dotted semibreve pulse.
[1.3] This phenomenon, where a musical ensemble moves from a state of one shared meter to a state of more than two meters in which all (or most) of those meters are experienced individually, is what I call “dispersed meter.” Dispersed meter differs from other types of rhythmically complex passages in the clarity with which each individual part expresses a reasonably stable projection of meter internal to itself. Examined in isolation (i.e., in the original partbooks each musician would have read from), each of the three non-cantus firmus parts in this Parsons passage is metrically clear and unambiguous, yet incommensurate with the others. It is only in attempting to grasp a global meter for this passage that the music appears overwhelmingly complex.
[1.4] Cohn (2016) has proposed a primary metaphor for the relationship of rhythm to meter: “centrifugal” rhythms undermine the meter, pulling the music apart, while “centripetal” rhythms resolve the tension and hold the music together. In an episode of dispersed meter such as the Parsons example above, the composite rhythmic texture could well be characterized as centrifugal, while at the same time, each of the individual polyphonic lines unambiguously points centripetally towards a single metrical organization. This tension between internally centripetal individual lines and an externally centrifugal musical whole, in which none of the metrical organizations of the various lines agree, is a defining feature of dispersed meter passages.
[1.5] The two techniques of rhythmic manipulation used to create this effect are similar to Krebs’s (1999) “grouping dissonance” and “displacement dissonance”; yet, because each part embodies its own local metrical reality, rather than being dissonant with the global meter, I find it more fitting to call them “regrouping” and “displacement” techniques. A global metrical view of the Parsons example might argue that, because the cantus firmus reinforces the metrical state of the tenor and represents a continuation of the earlier metrical organization, it should be analyzed as the “true” meter against which the altus and bassus parts are “dissonant.” Throughout this article, however, I will argue that adopting a more local and individual view of meter reveals more about these passages and is a perspective that reflects the performance practices and pedagogical experiences of the musicians who wrote, performed, and listened to these works.
[1.6] Rhythmic techniques such as regrouping and displacement cannot be isolated from melodic techniques of composition. One indication that composers intended the dispersed meter effect to be the primary focus of these episodes is found in how they alter their approach to counterpoint during them. Elizabethan polyphony is typically rich with melodic dissonances: suspensions, passing tones, and cross relations all add excitement and beauty to the counterpoint. In passages that utilize the techniques used to create dispersed meter (proportions, regrouping, and displacement), however, the vertical intervals among voices are almost entirely consonant. While it is possible that richly dissonant polyphony may be too technically challenging to compose when the parts rarely coincide rhythmically, the choice also leads to a satisfyingly reciprocal relationship between rhythm and pitch, where dissonance in one domain yields momentarily to dissonance in the other. Critically, contrapuntal dissonances and their characteristic treatments are laden with implied metrical information (e.g., suspensions point to stronger metrical positions with their dissonances and weaker ones with their resolutions). Reducing (or eliminating) dissonance in the pitch domain while highlighting it in the rhythmic domain means that no part’s internal meter is given additional metrical weight with dissonances or cadences. It also makes the rhythmic complexity of these passages more legible, as the ear is less distracted by voice leading and is able to focus entirely on the rhythmic texture. As Glareanus noted about Heinrich Isaac’s music, “It also gave him pleasure to show his versatility especially in tones remaining unchanged in any one voice, but with the other voices running about and clamoring around everywhere, just as the waves moved by the wind are accustomed to play about a rock in the sea” (Glareanus 1965, 473). For Glareanus (and presumably for other Renaissance listeners), relatively static vertical sonorities paired with lively rhythmic activity produced compelling musical passages.
[1.7] This article’s goals are twofold. On the one hand, I aim to explore the component rhythmic techniques of dispersed meter and what these disruptions can tell us about how metrical structures arise and function within Renaissance polyphony. The examples I foreground are extreme and sit at the chronological, geographical, notational, and stylistic margins—yet they nevertheless have something to tell us about the center of Renaissance music. By taking conceptual and technical elements of the Renaissance rhythmic idiom to or even past their logical extremes, these peripheral pieces illuminate the unwritten norms that operate in mainstream Renaissance works. On the other hand, while this study is deeply rooted in the Elizabethan repertory that I love, the issues with which it engages are much broader, namely the ways in which various and multiple views of meter can emerge within an ensemble performance. Despite a recent burgeoning of new metrical theory, much of this work represents an explicit (or assumed) listener/outsider theoretical perspective and does not address the important differences in cognitive, attentional, motor, and interpersonal experiences of meter between performers and listeners. In addition to examining moments where listener and performer perspectives of meter diverge in this music, this study attempts to take some first steps towards developing a theory of meter with musical performance at its center. Scholars of meter in other performer-driven genres and repertories such as jazz or heavy metal will have much to offer this endeavor.
[1.8] Finally, while there are other repertories which could probably exemplify many of these concepts, in the spirit of centering performance within this theoretical work, the examples I draw on are all pieces that I have inhabited deeply as a performer. And while I include many scores and some outsider perspective in my analysis, the theoretical exploration is also guided by my own phenomenological experience of meter in these works. Elizabethan polyphony is a non-continuous musical tradition that performers and scholars generally learn as a second language. I have thus also tried to highlight (as much as the historical record will allow) the voices and experiences of early modern theorists, composers, and performers who were native speakers of this style. Readers who are interested in the most broadly applicable ideas about meter may be most interested in sections 2, 4, and 9. Section 3 dives deeply into the details of this particular repertory, and sections 5–8 consider the specific rhythmic techniques individually and give examples. For those less familiar with mensuration, I begin the very next section with a short primer on this central topic.
2. Mensuration and Meter
Mensuration: a primer
[2.1] The term “mensuration” (i.e., measurement) refers to the hierarchical grid of note symbols that define the relationships between note values. Unlike modern musical notation, in which the relationship between note symbol and note value is fixed and defaults to binary (e.g., a whole note always contains two half notes unless a “tuplet” bracket or dot intervenes), mensural notation allows for either binary or ternary division of note values without altering the symbol of the note. A breve (double whole note), for example, may contain three semibreves or two semibreves, depending on whether the mensuration is perfect or imperfect at the tempus level. Likewise, the semibreve (whole note) may contain three or two minims depending on the perfection or imperfection at the prolatio level. The mensuration symbol designates these relationships, and also serves to indicate a likely value for the tactus, a marker of time usually embodied in a physical movement. The idea of the tactus is central to Renaissance music theory’s conception of musical time. Tactus is related but not identical to the modern concept of a beat. Not only was the tactus expressed through bodily movement, but it was also often conceived as motion (Grant 2014). Ruth DeFord (2015) notes that, in addition to movement, the tactus concept contains elements of both punctual and durational time. Though Graeme Boone acknowledges that early modern music theory “makes relatively little use of punctual concepts,” he also nonetheless argues “that punctual rhythmic hierarchy, functioning on multiple levels, is attributable to mensural music” (2000, 1 and 25). Both Boone and DeFord agree that the modern concept of ictus is possibly, though not necessarily, associated with the tactus.
Does Mensuration imply Meter?
[2.2] Whether mensuration’s hierarchical grid of note symbols also implies a hierarchical rhythmic structure akin to modern conceptions of meter is not a simple question. DeFord distinguishes between the notated mensural structure (which may define levels of rhythm that are not audibly present in a piece) and the “functional mensural structure,” which she defines as the audible rhythmic structure of the piece (2015, 50). Often the audible rhythmic structure of a piece and its notated mensural structure agree, as Boone has found in his analyses of the frequency of rhythmic onsets, what he calls initia. Other events with clear metrical implications in this style, such as cadences, suspensions, and simple syncopations, contribute to the sense of metrical structure, which often aligns with the mensural structure. DeFord has also highlighted the rhythmic aspects of melodic counterpoint itself, where the speed of the contrapuntal framework (as opposed to the nonstructural pitches which include dissonances) is directly related to the note value associated with what she calls the “compositional tactus” (2015, 84). The use of the punctus divisionis (a particular type of dot) to notationally separate mensural units known as “perfections” illustrates another way in which Renaissance composers understood larger metrical structures (Boone 2000; Kolb 2017). Similarly, Megan Kaes Long (2020) has described how multiple levels of metrical hierarchy and structure emerge from the schematic formulas used for setting Italian poetry.
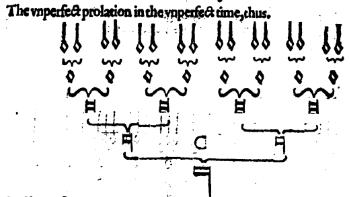
[2.3] Boone admits that the congruence between the metrical hierarchy that emerges from initia and the mensural grid breaks down somewhat in the sixteenth century, as the ![]() mensuration becomes ubiquitous and less predictive of audible metrical structures. Nevertheless, he argues that “the function of [that] signature does indeed seem to have been relatively weak in relation to the diversity of rhythmic patterning on certain levels; but this does not mean it had no hierarchical force” (Boone 2000, 36). Thomas Morley’s A Plaine and Easie Introduction to Practicall Musicke of 1597 explains that the
mensuration becomes ubiquitous and less predictive of audible metrical structures. Nevertheless, he argues that “the function of [that] signature does indeed seem to have been relatively weak in relation to the diversity of rhythmic patterning on certain levels; but this does not mean it had no hierarchical force” (Boone 2000, 36). Thomas Morley’s A Plaine and Easie Introduction to Practicall Musicke of 1597 explains that the ![]() mensuration (he calls these mensurations “moodes”) is not only the most common, but also the default, writing “This Moode is in such use, as when so euer there is no Moode set at the beginning of the song, it is always imagined to be this” (1597, 19). Morley further notes that, although
mensuration (he calls these mensurations “moodes”) is not only the most common, but also the default, writing “This Moode is in such use, as when so euer there is no Moode set at the beginning of the song, it is always imagined to be this” (1597, 19). Morley further notes that, although ![]() is technically a diminution of
is technically a diminution of ![]() mensuration (implying that the breve would be the tactus rather than the semibreve), “that rule be not so generally kept but that the composers set the same signe before songs of the semibriefe time” (1597, 23). The semibreve is, in fact, the most common value for both the compositional and performative tactus in the Elizabethan repertory considered here. Nevertheless, when transcribing these pieces and barring them in
mensuration (implying that the breve would be the tactus rather than the semibreve), “that rule be not so generally kept but that the composers set the same signe before songs of the semibriefe time” (1597, 23). The semibreve is, in fact, the most common value for both the compositional and performative tactus in the Elizabethan repertory considered here. Nevertheless, when transcribing these pieces and barring them in
Example 4. Edmund Fellowes (1948, 130). Example from Thomas Morley’s madrigal In dew of roses (note values original)
(click to enlarge)
Example 5. Otto Gombosi (1952, 166). Example from Jacobus Vaet’s motet Ecce apparebit Dominus
(click to enlarge)
[2.4] Many decades ago, both Edmund Fellowes (1948) and Otto Gombosi (1952) experimented with how to transcribe and visualize the metrical “irregularities” so typical of this style. Both tried barring the different voices of sixteenth-century pieces individually, rigorously following the internal rhythmic logic of each line. Fellowes also tried adding accent symbols to mark the beginnings of rhythmic groupings despite regular barring. The results of these experiments are quite busy and visually confusing in score format and perhaps more useful analytically than for performance. Fellowes’s example from a Morley madrigal (Example 4) appears to contain a fleeting moment of dispersed meter. Gombosi, discussing Vaet’s motets (see Example 5), captures the ambiguity of meter in this music when he writes that it:
clearly falls into larger metric units, not with the regularity of machine-made fabric, but with the irregularity of man’s handiwork that endows it with life…. There is no end to the diversity of configurations, to the innumerable solutions of the balance of tensions and compensations, to the variety of metric freedom within strictly defined, tightly constructed, wonderfully coordinated blocks. (1952, 167)
Example 6. Mallorie, Yf Man in Care, Add. MS 31390 f.22r (part 1)
(click to enlarge)
[2.5] Another potential pitfall of turning music written in ![]() into
into ![]() governs the entire piece (it’s way off to the left). Yet after the fermata in the middle of the first line of music, the metrical groupings are consistently six minims long rather than four (usually grouped as three semibreves but with some groups of two dotted semibreves). Here, the mensuration sign communicates the notational conventions clearly but offers little insight into the metrical groupings.
governs the entire piece (it’s way off to the left). Yet after the fermata in the middle of the first line of music, the metrical groupings are consistently six minims long rather than four (usually grouped as three semibreves but with some groups of two dotted semibreves). Here, the mensuration sign communicates the notational conventions clearly but offers little insight into the metrical groupings.
[2.6] A final mismatch between mensuration and meter is illustrated by the way composers sometimes write imitative motives where the same rhythmic gesture may begin on the on-beat or off-beat minim of a semibreve tactus, in what John Milsom (2005, 2016) has termed “stress-reversal.” While this term describes the compositional phenomenon well, I find it hides the problem inherent in performing these motives, where reversing the stresses is just one option (particularly when there is no text). In such cases, a performer must choose whether to alter the accentual pattern of the imitative point to fit it into a tidy metrical box or to keep the accentual pattern intact across imitative entrances, despite the metrical disruption it might cause. These issues are particularly acute in canons where the entries are spaced at very short intervals (like a minim), and the stress disagreements will last the entire piece.(5)
[2.7] So, while mensuration may be predictive of metrical structure, it is by no means determinative. This is especially true for late-sixteenth century pieces, which are most often notated in ![]() regardless of the metrical structure, and in which the metrical hierarchies of each line must be gleaned largely from context. Drawing on modern metric theory, Lerdahl and Jackendoff’s (1983) rankings of metrical preference rules provide some insight but require modification to fit this repertory. For instance, cantus firmus note values do in most cases provide an important clue about the prevailing larger metrical groupings, though the line itself tends not to project those groupings strongly.(6) Among the rules that Lerdahl and Jackendoff propose, the most directly applicable to parsing the metrical organization of Renaissance music are the preference for “strong beat early” (MPR 2), for longer note values in stronger metrical positions (MPR 5), and for onsets aligning with strong beats (MPR 3). Some rhythmic patterns are unambiguous in the metrical groupings they imply, while others are more flexible and can be heard in multiple ways. Due to the visual presentation of the music in parts and without barlines, the roles that individual musicians play in making sense of their rhythms and projecting those metrical interpretations in their performance cannot be overstated. Some of Lerdahl and Jackendoff’s (1983) further preference rules for how polyphony informs metrical parsing are also relevant. Cadences (MPR 7) and suspensions (MPR 8), for example, both provide important metrical information in this repertory. Then there is the trickiness of applying MPR 6, which privileges the metrical information conveyed by the bass over other lines. While the bassizans cadential voice, which leaps up a fourth or down a fifth, is a very common feature in this repertoire, it is really the cantizans cadential voice with the suspended dissonance that is the necessary signal of metrical arrival. Additionally, the imitative polyphonic texture asserts an equality between voices that I believe extends to their metrical importance. In episodes of dispersed meter, composers will avoid both cadences and suspensions in order to suppress those metrical cues.
regardless of the metrical structure, and in which the metrical hierarchies of each line must be gleaned largely from context. Drawing on modern metric theory, Lerdahl and Jackendoff’s (1983) rankings of metrical preference rules provide some insight but require modification to fit this repertory. For instance, cantus firmus note values do in most cases provide an important clue about the prevailing larger metrical groupings, though the line itself tends not to project those groupings strongly.(6) Among the rules that Lerdahl and Jackendoff propose, the most directly applicable to parsing the metrical organization of Renaissance music are the preference for “strong beat early” (MPR 2), for longer note values in stronger metrical positions (MPR 5), and for onsets aligning with strong beats (MPR 3). Some rhythmic patterns are unambiguous in the metrical groupings they imply, while others are more flexible and can be heard in multiple ways. Due to the visual presentation of the music in parts and without barlines, the roles that individual musicians play in making sense of their rhythms and projecting those metrical interpretations in their performance cannot be overstated. Some of Lerdahl and Jackendoff’s (1983) further preference rules for how polyphony informs metrical parsing are also relevant. Cadences (MPR 7) and suspensions (MPR 8), for example, both provide important metrical information in this repertory. Then there is the trickiness of applying MPR 6, which privileges the metrical information conveyed by the bass over other lines. While the bassizans cadential voice, which leaps up a fourth or down a fifth, is a very common feature in this repertoire, it is really the cantizans cadential voice with the suspended dissonance that is the necessary signal of metrical arrival. Additionally, the imitative polyphonic texture asserts an equality between voices that I believe extends to their metrical importance. In episodes of dispersed meter, composers will avoid both cadences and suspensions in order to suppress those metrical cues.
Metrical experience: whose experience is it?
[2.8] Many modern definitions of meter focus on the human perception of periodic rhythmic phenomena rather than on the sounds themselves or the notation associated with them. Justin London (2012, 65) has argued that “meter functions as a perceptual ground for rhythmic figures,” where the mind chooses the best metrical schema through which to parse the rhythms being experienced. Christopher Hasty’s (2020) approach, in which meter is the projection or expectation of rhythmic phenomena, is likewise perceptual but more malleable. Unlike London’s metrical templates, Hasty’s idea of projection is additive: each new piece of rhythmic information has the potential to alter or adjust expectations. In Hasty’s telling, there is no promise of cyclicity or evenness. Cohn (2020, 209) describes this perceptual turn as a break from the past in which “the terms, categories, and concepts of notation are overlaid upon, and often conceal, those of musical
[2.9] In my experience, Hasty’s projections, translated from the aural to the visual, provide a good model for playing this music. Musicians performing from notation are always negotiating meter on multiple timelines: reading precedes bodily movement and movement precedes hearing. The visual metrical projections made in real time by the musician translate into patterns of rhythmic emphasis and articulation in performance that, in turn, will shape how listeners (including the listening musician themselves) make metrical projections from the sound. Just as there are ambiguities in Renaissance music that require musicians to make in-the-moment choices about which pitches to alter, so too are there ambiguous rhythmic groupings that must be negotiated on the fly by the reader/player/singer.(8) Even the attention of a reading musician exists in at least two points in musical time simultaneously (or perhaps flickers back and forth between them): reading slightly ahead and planning; and listening slightly backwards and confirming/adjusting. For all these reasons and those explored in the next sections, the experience of, and indeed the reality of, meter differs between performers and listeners.
3. The repertory: proportions and pedagogy
[3.1] In Elizabethan music, episodes of dispersed meter are found most commonly in untexted polyphony, specifically, those pieces built on cantus firmi, a distinct but large subset of untexted works.(9) These types of pieces are extant in a limited number of manuscript collections (never in publications), and most were likely composed by a small, insular group of musicians writing for each other rather than for the liturgy, specific occasions, or patrons.(10) One reason these particular conditions provided fertile ground for rhythmic complexity is because performers and composers shared a pedagogical background not only in the theoretical study of proportions but also in the creative elaboration of chant.
[3.2] Despite the abolishment of Sarum Rite chant from the English liturgy during the Reformation, improvisation and composition over chant cantus firmi continued as core music pedagogical practices (Flynn 1993, 1995; Ludwig 2011).(11) There may not be many surviving documents related to the men who composed dispersed meter passages, but we can still make some observations about their musical culture. All were professional church musicians working in England’s most prestigious institutions, such as the Chapel Royal, St. George’s Chapel, Windsor, and Norwich and Ely Cathedrals. Many held positions as instructors of choirboys, and all would have received the typically rigorous musical training of choristers in their youth, including instruction on keyboards (and possibly on the viol as well) and improvisation/composition based on plainchant.
Example 7. The table book GB-Lbl Add. MS 31390, ff. 30v–31r
(click to enlarge)
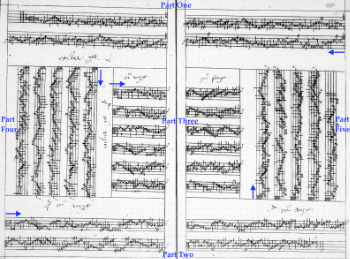
[3.3] Further inferences about their musical culture can be made from extant manuscripts, such as GB-Lbl Add. MS 31390 (the unique source for many dispersed meter pieces). Copied in “table book” format, with the individual parts oriented in the four cardinal directions (see Example 7), the format marries the convenience of partbooks for performance with the safety of containing all the parts in a single volume to prevent against loss. Since players or singers would sit around the table, the layout of the parts in the book prescribes and preserves the expected spatial arrangement of bodies. As Rastall (1997, 2022) has shown, the Elizabethan norm was to separate parts that have similar ranges. This layout, which increases the audibility of the individual lines and reduces “blend,” is thus quite different from modern musical values and layouts.(12) Similarly, this notational format prescribes a closed circle of musicians, admitting no opening towards an audience. When my consort recorded an album of pieces from Add. MS 31390, we did so in the round and in the orientation required by the manuscript (LeStrange Viols 2018). Such an arrangement maximized the sense of individual independence by letting us step outside the boxes of tessitura and hierarchy of importance implied by traditional highest-to-lowest arrangements. Our most successful concerts of this music were also performed in a closed circle with the audience around us on all sides. The closed circle is a good metaphor for this music. This repertory is inward facing: the primary audience was often the players themselves, many of whom were likely composers as well (Ludwig 2011; Weiss 2021).(13)
Example 8. GB-Lbl R.M.24.d.2, f.101r
(click to enlarge)
[3.4] Lastly, an important part of the pedagogical experience that composers of dispersed meter shared was the study of proportions. For Renaissance theorists and composers, rhythmic proportions neatly mirrored the harmonic proportions that defined musical intervals, and so durational proportions were often given extensive treatment in theoretical treatises. For example, John Dygon’s (2006) early-sixteenth century treatise (a transmission and expansion of Gaffurius’s proportion examples from his 1496 Practica Musice [Gaffurius 1993]) and Thomas Morley’s (1597) lengthy treatment of varying notations for proportions, both highlight the theoretical and practical importance of proportions in English music of this period. English musicians of the sixteenth century, more than those on the Continent, were interested not only in studying proportions but also in composing them. Some proportion pieces draw on the deliberately cryptic notations of quadrivial music theory (known as “speculative” music) but was nevertheless intended to be performed (as “practical” music), often in copies that were translated into simplified musical notation (Bray 1995). This so-called musica speculativa is perhaps best understood as an audible instantiation of music theory. By sequentially layering simple proportional relationships like sesquialtera (3:2), tripla (3:1), or dupla (2:1) English composers were able to guide performers into complex rhythmic relationships between voices (such as 9:8 or 6:4), a technique known as induction.(14) While the more extreme examples of proportions found in Dygon may not have been meant to be performed, similarly complex proportions (see Example 8) found in the Baldwin Commonplace Book (GB-Lbl R.M.24.d.2), owned and copied (and in many instances composed) by John Baldwin may well be, as these skills, connected to the English university music curriculum, held great prestige value among musicians (Bray 1995, Fallows 1996, Heminger 2018).
Example 9. GB-Lbl R.M.24.d.2, f.103r
(click to enlarge)
[3.5] The Baldwin Commonplace Book contains proportion pieces both by Baldwin himself and by Nathaniel Giles, his colleague at St. George’s Chapel, Windsor. Giles served as Master of the Children (meaning he was in charge of the musical education of the choirboys) both at Windsor and then later also at the Chapel Royal. One proportion piece found in the Baldwin Commonplace Book (seen in Example 9) seems to have been composed by Giles as an exercise for students. The inscription at the end of the duo reads, “a lesson of descant of thirtie eighte propor[t]ions: of sundrie kindes: made by Mr. Giles m[aste]r of the children of Windsor then: & now m[aste]r of ye children of ye chappell also.”(15) This duo is on the Miserere Mihi, a popular cantus firmus for teaching descanting and canonic techniques (Danner 1967; Collins 2007).
Example 10. GB-Lbl R.M.24.d.2, f.102v
(click to enlarge)
[3.6] The use of proportions in this duo is entirely systematic and uses the process of induction to guide the student from simpler rhythmic relationships to complex ones, often returning briefly to “proportio equalis” between each excursion. The cantus firmus part consists of equal semibreves, and the numerical proportion ratios can all be understood as describing how many notes in the florid part fit against how many cantus firmus notes. One such excursion, seen in Example 10, begins with 5:1, or five notes for each cantus firmus note (marked A in the example). The next proportion, 5:2, asks the student to double the length of their notes so that two cantus firmus notes pass for each of their groups of five (marked B in the example). A further doubling of length (5:4) follows at letter C. The final proportion of this set (letter D) now requires the student to subdivide each of their long notes in three to achieve an impressive 15:4 proportion against the cantus firmus.(16)
[3.7] While some of the proportions found in the Baldwin Commonplace Book may straddle the boundaries between speculative and practical music, episodes of dispersed meter reside comfortably within the sphere of practical music. Dispersed meter and its constituent techniques, nevertheless, are still related to this tradition of composing proportions as well as other practices of rhythmic generation and complexity, all of which were emphasized within music pedagogical traditions of the time.
4. A Performer-Oriented Analytical Perspective
Example 11. Brewster In Nomine a4
(click to enlarge)
Example 12. Brewster In Nomine a4
(click to enlarge and listen)
[4.1] Several factors make this repertory ideal for performer-oriented analysis. As already mentioned, the social context in which Elizabethan untexted polyphony was composed and presumably played was not focused on performance for outside listeners.(17) Secondly, the pieces are transmitted almost exclusively in notational formats other than scores, where the material and visual experience of a single part contributes much to the experience of reading, singing, or playing from it and there is valuable information to be gained from approaching the music from a partbook perspective (van Orden 2015). Even the process of composition rarely involved scoring up the parts (Owens 1998). The limited view of the musical composite provided by reading from a part can actually make the performance of rhythmically complex passages simpler by hiding the composite complexity from the reader; though it also requires strong rhythmic independence on the part of the reading musician. Take, for example, this passage from the In Nomine a4 by Brewster. Example 11 shows a transcription of the four individual parts, while Example 12 shows a score transcription. When reading from a part, the transition from minims to dotted minims is quite simple for each musician to accomplish. Reading from the score reveals the complexity with which the lines are interleaved but the barlines only introduce distraction as they interrupt the rhythmic groupings of the parts. Similarly, the large table book format of Add. MS 31390 inscribes not only the spatial layout of its readers, but also the degree of intimacy. When I have brought a to-scale facsimile of this manuscript to class, students are surprised (and perhaps a little embarrassed) by how tightly they need to squeeze together to read even a five-part piece, let alone a six-part one. Singers find their faces are much closer together than expected, and viol players must angle themselves carefully and work to avoid hitting each other or the table with their bows.
[4.2] Finally, these pieces’ compositional style points to both independence and cooperation between the parts and musicians. Imitative polyphony affirms the equal importance and contribution of every line to the whole by passing motivic material (the contrapuntal “point”) from part to part while simultaneously requiring collaboration among them. Imitation is definitionally a response; thus, by asking each part to “say” something that has already been said, this kind of writing embeds social interactions into the notation. For example, a point that is imitated verbatim at the same pitch level inscribes a different relationship between the players or singers than does a point that in its imitation extends the phrase to add a new musical thought. This particular configuration of independence and interdependence also applies to the melodic content of a piece. The very pitches to be sung or played are often contextually affected both by the voice leading internal to that part (e.g., adding a flat to avoid leaping or outlining an imperfect fourth or fifth) as well as by its relationship to other parts (e.g., adding a sharp to a cantizans figure to make an authentic cadence against another part). Why, then, should we not conceive our analysis of rhythm and meter in this repertoire in terms of highly independent parts as well? Even in “normal” passages, the Elizabethan musical idiom is rich with syncopations and unexpected accentuations that excitingly pull and push against the fabric of shared meter. In passages of dispersed meter, that fabric temporarily dissolves and the musicians must be metrically independent in perfect parallel so that they may reconvene at the end of the episode. As I have argued elsewhere in similar repertories, analyzing imitative polyphony from a partbook perspective can reveal humor, wit, and meanings that might otherwise be obscured from an outside or global perspective (Weiss 2020). In the case of dispersed meter, a global perspective unavoidably aims to impose a hierarchy of importance on what I argue is best seen as a pluralistic experience of meter.
[4.3] There are, of course, many additional reasons why a performer-oriented analytical perspective of meter may be advantageous. Kozak’s (2020) work on the embodied experience of time offers an exciting direction, though his focus, again, is explicitly on listeners.(18) However, the embodied and cognitive experience of creating sound is often different than the experience of listening to that sound, which is different again from reading a score and imagining that sound. While my analysis here explores these differences in the context of a notated musical tradition, the performer’s engagement with the notation is not the sole defining aspect of these differences. Performances in which musicians engage with memorized musical templates or remembered possibilities of musical direction require similar cognitive demands.
[4.4] While a listener hearing Elizabethan polyphony will hear all the parts of the music more or less equally, a performer of this music (with the exception of lutenists and keyboard players) will have a special inside relationship with the individual line of music they are reading and playing/singing. Their experience of meter is thus some combination of engagement with the whole and engagement with their own line. When reading notation with barlines—and with note spacings optimized to an invisible grid within—rhythm is usually read both backwards and forwards from the barlines. This fact is quickly revealed when you hand an adept modern player a part without barlines and without modern spacing conventions: nearly always, it turns out they are not fluent at distinguishing the graphical difference between a whole rest and a half rest but rather infer them from the context of the barlines. Conversely, reading rhythms without barlines is a more additive process.(19) This makes it easier to switch rhythmic groupings because the notation doesn’t provide any visual resistance through the metrical units implied by barlines. Performers reading notation also have a different set of rhythmic projections than listeners do because reading usually involves glancing slightly ahead of the notes currently being sung or played. If I am reading a string of minims and see that two notes from now my part switches to dotted minims, I can alter my projection to prepare for that change of pulse. This dual attention to a metrical present and a metrical future is not available to a listener on a first hearing.(20) Another aspect of a musician’s attentional engagement with notation are the active choices they can make about how to group the note values they see. As many researchers have pointed out, these choices can have a significant effect on the audible perception of the meter (DeFord 2015; London 2012; Kozak 2021).
[4.5] In addition to the visual engagement with their individual notated part, a musician also receives metrical information kinesthetically through the physical motions they make to create the sound. This kinesthetic feedback no doubt both reinforces and complicates their experience of meter. In the case of a viol player, the bow arm and hand travel back and forth with the surface rhythms of the piece.(21) A wind player’s tongue articulates each note with various syllables, which combined with air differentiates the stronger and weaker ones. A singer may follow the emphasis of the text—which may clarify or obscure metrical information from the musical notation. When these physical actions are aligned with the musician’s sense of the meter, they strengthen it. But attempting to hold onto a metrical organization that is being contradicted by the movements of your own body can become quite difficult. To give an example, I have taught Elizabethan repertoire at many viol workshops and have found that when players initially encounter a regrouped passage with a long string of ternary units within a predominantly binary texture, they start furiously tapping their toes to the binary pulse, desperate to physicalize the binary meter they’re trying to hold onto despite the contradictory information in their part. The first thing they need to learn is to allow themselves to feel the ternary groups metrically and in their bodies—while remaining rhythmically accurate enough to stay together with the rest of the ensemble. The ability to feel and play the metrical hierarchies of one’s own part while not losing coordination with others who are experiencing a different metrical organization or the same metrical organization displaced in time requires a great deal of metrical independence. This extreme independence of voices also gives rise to a sense of agency within the performers inhabiting these individual polyphonic lines.(22)
5. Regrouping
[5.1] A major characteristic of Renaissance rhythm is the fluidity of rhythmic groupings, and the ease with which these groupings can depart from metrical expectations. The insertion of one or two ternary groups within a predominantly binary texture is extremely common, yet early modern theorists do not provide terminology for it (McGuinness 1994). So despite there being a large body of scholarly work on mensuration symbols and the concept of the tactus (Busse Berger 1993; Grant 2014; DeFord 2015), the surface rhythms of Renaissance music and their relationship to the hierarchical structures of meter remain undertheorized in both the primary and secondary literature. Because of this, the people who have the greatest experience with these rhythmic manipulations are often performers, and they have developed their own idiosyncratic vocabulary for them. Robert Eisenstein recalls that when he sang with Richard Taruskin’s ensemble Cappella Nova, they would refer to ternary groups within a binary texture “as Bye-ums, where ‘Bye’ would be, say, a quarter note, and ‘um’ would be an eighth note in the ¼ reduction of original note values R[ichard] T[aruskin] favored in his transcriptions” (Personal communication). The concept of regrouping provides great clarity in naming these rhythmic manipulations.
Example 13. Thomas Morley A Plaine and Easie Introduction (1597), pg. 89
(click to enlarge)
[5.2] Of course, examples of regrouping do show up in the theoretical literature, often as rhythmic patterns that can be used when improvising descants against cantus firmi. Thomas Morley describes both the rhythmicization of chant notes—including alternating long and short notes to create ternary groupings and giving the chant notes unusual lengths such as five minims (a technique we’ll encounter below)—as well as rhythmic patterns which can be used for a descant above or below a simple chant cantus firmus in semibreves (he calls these “waies”).(23) Just as in the rhythmic patterns for chant, those for descant include ternary groups, though now four of these ternary groupings fit against three of the semibreves of the cantus firmus. Charles Butler—a music theorist, priest, beekeeper, and grammarian who advocated a system of phonetic English spelling—copied several of Morley’s examples of “waies” verbatim in his 1636 treatise The Principles of Musik, including the one found in Example 13. Butler, however, changed the terminology and presents the patterns as “4 special ways” of syncopation at the minim level (1636, 68).(24) I will discuss these examples and the concept of syncopation in section 6.
Example 14. Pretty Wayes. GB-Lbl Add. MS 29996 f.195v
(click to enlarge)
Example 15. Pretty Wayes. GB-Lbl Add. MS 29996 ff.196r
(click to enlarge)
Example 16. Pretty Wayes. GB-Lbl Add. MS 29996 ff.192v
(click to enlarge)
[5.3] Another pedagogical example of rhythmicized descant comes from the manuscript GB-Lbl Add. MS 29996, compiled over time from the mid-sixteenth to the early-seventeenth century; it contains many keyboard pieces and pedagogical works. The manuscript’s earliest layer is connected to John Redford, Master of the Choristers at St. Paul’s during the end of Henry VIII’s reign, while later layers include the hand of Thomas Tomkins. One entry in this book is a set of sixteen short anonymous pieces titled “Pretty wayes: For young beginners to looke on” which exemplify many different rhythmicized descants over a single short cantus firmus (Miller 1947). These “wayes” include ternary groups similar to Morley’s, created from long-plus-short and short-plus-long (Example 14). Another uses proportional notation to achieve a 4:6 proportion with the cantus firmus (Example 15), while a third achieves the same proportional relationship through note values alone (Example 16). The use of such standard and repeating rhythmic patterns in pedagogical materials suggests that these rhythmic techniques of improvisation/composition were ones that adult Elizabethan musicians and composers would have been well familiar with.
Example 17. William Mundy In Nomine a5
(click to enlarge)
[5.4] Text emphasis appears to drive the motivation for regrouping in texted music. Even when the text is not presented homophonically, each voice will have the same text. In untexted music, there appears to be freedom for a wider variety of rhythmic approaches among the voices. For example, in William Mundy’s In Nomine a5 no. 1, there is a passage where a single part (the top voice) has a long sequence of unambiguous ternary groupings within a predominantly binary texture (see Example 17). The onset of this grouping change is highlighted by simultaneous and aligned ternary groups in the lowest voice (which peter out after just four groups), while the other non-cantus firmus voices remain in groupings that are clearly binary despite containing syncopations. In such an instance where a part consistently switches from binary to ternary groupings (or vice versa), the effect may straddle the line between regrouping and proportions—both of which can achieve the same musical result. The distinction between proportions and grouping changes may be understood as largely notational, with altered note values indicating groupings and mensuration or proportion signs indicating proportions.
Example 18. Christopher Tye O lux beata Trinitas mm. 47–58, part three
(click to enlarge)
[5.5] Regrouping need not be consistent, however. A more complicated example comes from one of the voices of Christopher Tye’s O lux beata Trinitas shown in Example 18. Though I have not added barlines, each breve duration is marked by a bar number. To orient yourself, I recommend calibrating your sense of meter with the cadential suspension/syncopation that resolves at breve 48. Beginning at breve 52, I’ve marked what I feel are ternary groups with brackets and binary groups with carets. Do note the ambiguity of the rhythmic groupings of those first two brackets. Playing the part alone, I might not choose to play those as groups of three, but in the context of hearing all the parts, it becomes clear that the material at breve 52 is a motivic imitative entrance that is ternary. At the same time, hearing all the parts together creates additional difficulties in playing this excerpt (a score can be seen in Example 24 below). The top part plays consistent ternary groups from halfway through breve 52 to the end, a proportional shift that expresses a single clear sense of meter. This part, however, never settles into a pattern that allows the player to predict the next grouping. To borrow Cohn’s (2001) metaphor of the skier, this part is like skiing a slalom, veering between binary groups to one side and ternary groups to the other unpredictably.
Example 19. Robert Parsons Ut re mi fa,
(click to enlarge)
[5.6] I suggested earlier that the distinction between regrouping and proportions is largely notational, but even so it is sometimes an ambiguous distinction. A strict and stable regrouping episode, such as that found in the Parsons example at the opening of this article, is functionally identical to a proportional change—and indeed, the bass part of the Parsons begins this episode with a new mensuration sign and a string of perfect semibreves in ligatures. However, the two other voices do not have a mensuration sign and indicate the change only through note values (see Example 19). The three parts of the Parsons sound identical but are notated differently. In contrast, in episodes like the Tye O lux in Example 18, notating the regrouping using only note values allows for more complex non-periodic rhythmic interplay in which binary groupings are irregularly interpolated among the regrouped ternary patterns. So, while the audible, metrical effect of regrouping may be a proportional relationship, the notational flexibility of the mensural system allows Elizabethan composers to make a distinction between proportions created through “extrinsic” notational features such as mensuration signs and proportion symbols, as well as “intrinsic” notational features such as note values and coloration (empty or filled noteheads in this repertory).(25)
Example 20. Christopher Tye In Nomine a5 Seldom Sene, mm. 33–41 (Audio: The Spirit of Gambo 2014)
(click to enlarge and listen)
[5.7] Another rare example in which regrouping is treated explicitly as a proportion and marked with extrinsic symbols can be found in Christopher Tye’s appropriately titled, In Nomine Seldom Sene (see Example 20). Here, three different symbols (and also coloration) are used to indicate the same sesquitertia (4:3) proportion.(26) The majority of examples, however, use intrinsic notation only, leaning heavily on the metrical ambiguity available through this kind of notation. John Baldwin seems to have recognized the commonality of proportion and regrouping but also their distinction.(27) Baldwin’s In Nomine a4, which contains a dispersed meter episode including regrouping, appears in his commonplace book in the subsection devoted to proportion pieces. The regrouping, however, is notated without proportion signs and only through note values. Conversely, Baldwin’s In Nomine a5, which includes a canon but no dispersed meter, appears separately in a different subsection of the book.
Example 21. Blankes A Phancy, mm. 13–19 (LeStrange Viols 2018)
(click to enlarge and listen)
[5.8] In the Mundy passage in Example 17, Krebs’s terminology of “grouping dissonance” does capture something about that individual part and its oppositional relationship to the metrical consensus of the other parts; however, in other examples of regrouping, the idea of metrical dissonance against a global meter is counterproductive. The following excerpt from Blankes’s A Phancy in Example 21 shows a passage in which prevailing binary groupings give way to homorhythmic ternary groups in all five parts, creating a temporary but total reorganization of the metrical environment. The effect created is of a sharp metrical change, and a unanimous one at that. Yet if there is any metrical dissonance here, it can only result from the expectations projected from the prevailing binary meter of breve thirteen. That the composer himself conceived of this as a metrical shift is strongly evidenced by the impossibility of barring this passage in duple breves or semibreves. In my transcription in Example 21, bar 16 is missing a semiminim in order to keep the bars in alignment with the metrical stresses. I have added brackets only to the top voice since all five are in rhythmic unison.
[5.9] This passage is also noteworthy for the complicated questions it provokes about the performance of notated mensuration changes. Without the homophonic grouping change, in moving from ![]() to
to ![]() (or
(or ![]() ), one would expect the semibreve tactus to continue unchanged, but now be subdivided into three minims rather than two (i.e., the minim speeds up). Yet when the mensuration change is approached in this way from a regrouping episode, it is very tricky to make this sesquialtera (3:2) shift and have the identical rhythmic patterns suddenly speed up when the notation changes. Moreover, the non-uniformity of placement of the mensuration sign in the individual parts also hints towards a performance in which the note values continue at the same rate of speed, as if the perceived tactus had already shifted to encompass the three semiminim groups of notes found in the homophonic regrouping.(28) Lastly, there is also a subtle return to binary groupings just before the return to
), one would expect the semibreve tactus to continue unchanged, but now be subdivided into three minims rather than two (i.e., the minim speeds up). Yet when the mensuration change is approached in this way from a regrouping episode, it is very tricky to make this sesquialtera (3:2) shift and have the identical rhythmic patterns suddenly speed up when the notation changes. Moreover, the non-uniformity of placement of the mensuration sign in the individual parts also hints towards a performance in which the note values continue at the same rate of speed, as if the perceived tactus had already shifted to encompass the three semiminim groups of notes found in the homophonic regrouping.(28) Lastly, there is also a subtle return to binary groupings just before the return to ![]() , a common pre-cadential hemiola but one which conveniently segues into the next section if the semiminim remains constant.
, a common pre-cadential hemiola but one which conveniently segues into the next section if the semiminim remains constant.
Example 22. Typical regroupings found in ![]() and
and ![]()
(click to enlarge)
[5.10] Early modern music theory’s concept of hemiola does provide some perspective on regrouping, but most regroupings in this repertory do not produce hemiolas. As discussed in treatises, the 3:2 proportion described by a hemiola is generally at the level of the tactus. DeFord defines a hemiola as consisting “either of three time units on two ternary tactus
6. Displacement and Syncopation
Example 23. Thomas Morley A Plaine and Easie Introduction (1597), p. 152
(click to enlarge)
[6.1] The displacement of binary groupings, which can easily be referred to as syncopation, is extremely common in Renaissance music. Some of the most obvious and important metric signaling information in this repertory comes from the syncopated dissonance that immediately precedes a cadence; indeed, this is the context in which Morley talks about it most. Morley explains, “for a Cadence must alwaies bee bound or then odde, driuing a small note through a greater which the Latines (and those who haue of late daies written the art of musicke[)], call Syncopation, for all binding and hanging vpon notes is called Syncopation” (1597, 152). He even suggests that syncopated dissonance is so deeply associated with the cantizans voice of a cadence that the two terms are nearly synonymous, referring to “Syncopation (which wee abusiuly call a Cadence)” (1597, 144). Morley’s non-cadential examples of syncopation or “driving” show long strings of simple displacements of binary groups, as seen in Example 23, first at the semibreve level, then at the minim level. DeFord documents two meanings of the term syncopation within the Renaissance music theoretical literature. The first refers to “complete time units that are interrupted by other complete time units on the same mensural level,” and the second, more in line with our modern usage, applies when “only the displaced notes are called ‘syncopated’” (2015, 42–43).
[6.2] Displacement of ternary groups, however, differs significantly from that of binary groups, both because it can involve three polyphonic voices rather than two and because it is easier for the displacement of the voices to shift in relation to each other throughout the episode. I will argue that dispersed meter episodes should be understood as distinct from syncopation, although displacement can be a feature of both. In Elizabethan untexted polyphony, the displacement of ternary groups almost always occurs within the context of a regrouping episode, adding to its potential for metrical disruption. This tendency in particular makes Krebs’s (1999) terminology of “displacement dissonance” and his labeling scheme for it less useful for this repertory. Even if we attempt to analyze the music from the perspective of a global meter, that meter may be binary and is often perceptually outweighed by the two or three regrouped and subsequently displaced voices. If the only voice still participating in the original global meter is the cantus firmus (as can be the case in dispersed meter episodes), then that global meter is no longer fully present and is not a useful reference point for analysis. Here, the voices are dissonant against each other rather than against some prevailing metrical framework.
Example 24. Christopher Tye O lux beata Trinitas, mm. 48–end (Audio: LeStrange Viols 2018)
(click to enlarge and listen)
[6.3] Insofar as it captures the relationships of the individual voices, which, to me, is the central feature of this technique, the term displacement proves itself to be of value. Indeed, in cases where we might describe a voice’s displacement as constantly shifting, this terminology reflects the metrical disjunction between the individual parts without privileging one perceptible meter over another. Previously, we looked at the third voice of Christopher Tye’s O lux beata Trinitas; now, let’s look at the full score for this passage. In Example 24, I have placed brackets (for ternary groups) and carets (for binary groups) over voices one and three; voices four and five are also primarily in ternary regroupings but these are twice as slow. Beginning on the third minim of measure 52, the top voice has consistent ternary groups until measure 57. The third voice also has many ternary groups from the beginning of measure 52, but also several binary groups interpolated among them. These binary groups cause the displaced relationship between the two voices to frequently shift: sometimes one is leading, and sometimes the other.
[6.4] The rhythmic and gestural independence between these two voices is surprisingly difficult to capture in performance. When LeStrange Viols recorded this piece, I found myself playing the third voice and struggling to carve out these binary and ternary shapes without losing coordination with my colleague playing the top voice. My most successful takes happened only when I was able to turn off my internal metrical expectations and take a more nearsighted approach, playing whatever grouping was in front of me without attempting to guess what came next. (The experience it most reminded me of was sight reading tablature in a new tuning where one can’t yet predict which frets will yield which pitches.) In situations like this, as readers may have experienced, the analytical/expectational part of the mind goes quiet, and the fully formed melodies or metrical patterns emerge only in the rear-view mirror.
[6.5] The displacement of ternary groups usually results in an episode of dispersed meter because, as mentioned above, this type of displacement is strongly associated with ternary groups created through regrouping—even when the prevailing global meter already includes groups of three. This “double disruption” to the metrical environment (regrouping plus displacement) results in an especially strong sensation of dispersed meter as it maximally undermines any sense that there is a single metrical grid or unifying, composite tactus.
Example 25. John Baldwin In Nomine a4,
(click to enlarge and listen)
[6.6] When ternary groupings are displaced at the same mensural level simultaneously in three voices, the result is a special phenomenon I call fully saturated displacement. The Parsons Ut re mi fa in Example 3 provides a clear instance of this effect. Another striking example of fully saturated displacement occurs in John Baldwin’s In Nomine a4, which opens uniquely in medias res with a regrouping and displacement episode and only begins resolving into the notated (and predominant) metrical organization in measure seven (see Example 25). Composers’ clear preference for double disruption when using displacement provides evidence that the dispersed meter effect is a deliberate goal in these passages. For example, if displacement occurred at a metrical level that was already ternary (such as the minims in the Baldwin example), it would be easier to imagine that one of the three displacements would feel aligned with a global meter and the effect of dispersed meter would be weaker. However, if the clear sense of a single tactus is already disrupted by regrouping, then each voice’s further displacement becomes equally plausible. In Krebs’s (1999) terms, it erases the possibility of any tension between “metrical” and “antimetrical” layers, making it impossible for an outside listener to identify any solid metrical hierarchy against which one layer is dissonant. Who is to say which of these three voices is on the grid and which two are displaced? Or, has the audible grid itself switched to a ternary organization (even though in other examples there are still voices projecting clear binary groupings)?
[6.7] Baldwin has taken additional steps in preventing any of the three regrouped parts from sounding aligned with a global meter by not bringing in the top voice on the downbeat of the piece and by making all three parts slightly irregular and pattern resistant via a smattering of undotted minims. Indeed, the top voice is even marked as optional (“triplex ad placitum”) with the cantus firmus onsets preserving much of the displacement texture. Listening to the opening of the Baldwin, the ear struggles to find larger metrical structures and is forced instead to grab onto the composite semiminim pulse, which is uncomfortably fast for a tactus and which lacks any related, secondary pulse to create a hierarchical sense of meter. Nevertheless, playing this opening from partbooks is not uncomfortable at all. Like a wind-up toy, once started, it easily continues, with each musician fully within their own metrical environment. The surprise and pleasure of reconvening with parallel tenths between voices one and three as metrical disruption resolves into order in measure 7 is the most joyful moment of this piece.
Example 26. Charles Butler The Principles of Musik, pg. 69
(click to enlarge)
[6.8] Cohn (2020) argues that displacement should fall within the conceptual category of syncopation. When analyzed from the perspective of compositional mechanics, this makes sense, although from the perspective of a performer I find the experience distinctly different. Morley’s discussion of syncopation does not include ternary groups; in contrast, Charles Butler’s (1636, 68) transmission of Morley’s rhythmicized “wayes” for descanting over a cantus firmus are indeed included in a section about syncopation (see Example 26). Butler’s discussion of this technique goes no further, however, and I know of no other historical discussions that refer to these techniques as syncopation. Pace Butler, the displacement of ternary groups is, to my mind, conceptually and functionally distinct from early modern theoretical conceptions of syncopation. DeFord hints at this distinction when she notes that “syncopation is meaningless as a rhythmic technique unless performers and listeners perceive the distinction between rhythms that conform to the mensural structure and rhythms that conflict with it” (2015, 98). In other words, surface rhythms can either fit within or push against the mensural grid, and these two functions must be distinguishable. A simple duple syncopation, as in Morley’s examples, does just that: it pushes against the grid, but never actually threatens the grid’s stability or audibility. In fact, these simple syncopations actually reinforce the mensural grid by briefly pulling against it and then satisfyingly snapping back into place (or “relocking,” to use Cohn’s terminology). Maria Witek (2017) documents the body’s desire to “fill in” beats left unemphasized by syncopation, reinforcing physical entrainment to the global metrical structure.
[6.9] In contrast to these conceptions of syncopation, displacement of ternary groups generally does not reinforce the mensural grid through momentary dissonance with it, but instead dissipates the grid into a competing set of metrical frameworks before eventually reconvening on a shared sense of meter. This is a meaningful distinction and a useful one. True syncopation creates metrical clarity by ultimately reinforcing metrical hierarchies; on the other hand, displacement of ternary groups, particularly fully saturated displacement, typically does the opposite. This is especially true for Elizabethan untexted polyphony, where the propensity for double disruption means that ternary displacement occurs mainly during regrouping episodes where the original sense of meter is already difficult to locate.
7. Serialized Rhythm
Example 27. Fernando de las Infantas Plura Modulationum (1579), mm. 1–7.
(click to enlarge)
Example 28. Thomas Morley A Plaine and Easie Introduction (1597), pg. 16
(click to enlarge)
[7.1] Dispersed meter is not the only way Elizabethan composers created metrical complexity. Another contemporary technique found in untexted cantus firmus pieces is serial rhythm, in which each part is assigned a single note value for the duration of the piece, and each part has a different note value from the others. These pieces can be understood within the context of speculative music, a kind of “composed music theory,” in which serialized rhythms act as musical proofs of notational proportions that mirror the visualizations found in music theoretical treatises. Compare, for instance, the Infantas composition in Example 27 with Morley’s illustration of the ![]() mensuration in Example 28.(29)
mensuration in Example 28.(29)
Example 29. Shelbye Miserere, GB-Lbl Add. MS 30513, f.47v
(click to enlarge)
Example 30. Picforth In Nomine, mm. 1–9 (Audio: LeStrange Viols 2018)
(click to enlarge and listen)
[7.2] While Continental examples of serialized rhythm employ note values with exclusively binary relationships, English musicians preferred to mix binary and ternary subdivisions, using this technique as musical proof of more complex proportional relationships. These works generate static polyrhythmic/polymetrical textures that can be notated either through proportions, as in Example 29, or with note values alone, as in Example 30 (similar to grouping changes). There are a small handful of examples: both Shelbye’s Miserere setting in the Mulliner Book (Example 29) and Morley’s “Cross Canon” from the Plaine and Easie Introduction make use of serialized rhythm (the latter in combination with unserialized rhythm) that includes both ternary and binary proportions. Yet perhaps the best-known example of the serialized rhythm technique is the Picforth In Nomine (Example 30), found uniquely in GB-Lbl Add. MS 31390.
Example 31. Picforth In Nomine notated with proportions, mm. 1–9
(click to enlarge)
[7.3] Although ![]() appears at the beginning of the second voice of the Picforth, it is more suggestive of the groupings than notationally functional and does not affect the part’s note values; the line can be read as if it were in
appears at the beginning of the second voice of the Picforth, it is more suggestive of the groupings than notationally functional and does not affect the part’s note values; the line can be read as if it were in ![]() like the rest of the voices. The flexibility of the mensural notation system means that this type of piece could be notated entirely with proportion signs rather than note values, but as you can see in both the Shelbye and Picforth above, the notational emphasis is on distinguishing the parts. To show what the Picforth might look like if it were notated with proportions only, I have created, in Example 31, a speculative notation for the piece, borrowing proportion notation conventions from both Thomas Morley and John Baldwin.
like the rest of the voices. The flexibility of the mensural notation system means that this type of piece could be notated entirely with proportion signs rather than note values, but as you can see in both the Shelbye and Picforth above, the notational emphasis is on distinguishing the parts. To show what the Picforth might look like if it were notated with proportions only, I have created, in Example 31, a speculative notation for the piece, borrowing proportion notation conventions from both Thomas Morley and John Baldwin.
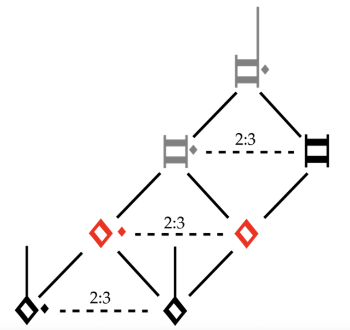
[7.4] Because each part contributes only a single isochronous pulse, none of these parts can be said to individually project a hierarchical meter. Similar to distributed cognition, each voice presents a metrical building block, and only through their combination do meters arise. Multiple meters can and do emerge from the interactions of two or more of the parts, but these interactions are more contingent than authoritative. For instance, when looking at the score in Example 30, the minims of the top voice can be understood as a binary subdivision of voice three or as a ternary subdivision of voice five. A performer can choose to project either of these metrical interpretations, or even switch between them, by grouping the string of notes through articulation (discontinuity) and emphasis. These choices about how the parts relate to each other will influence how a listener hears the resulting rhythmic matrix. Nevertheless, it is hard to avoid the feeling that the two competing tactus pulses, semibreves and dotted semibreves, create a polymetrical environment—particularly since the interval at which all five voices align (three breves, or approximately five seconds) is beyond the perceptual limits for hearing a pulse (London 2012).
Example 32. Ski Hill Graph of Picforth In Nomine. Note values not represented in the piece are colored grey
(click to enlarge)
[7.5] Another way to visualize the rhythmic matrix of the Picforth is through one of Cohn’s (2001) ski-hill graphs (see Example 32), which models the possibilities for interpreting individual note values within multiple metrical arrangements. Stephen Malinowski, the creative force behind the Music Animation Machine web channel, has also created at least eight different animated visual analyses of this piece to accompany LeStrange’s recording that highlight the rhythms created by this technique; they are highly worth watching (see link). There are also several recordings of this piece that differ remarkably, each emphasizing a different reading of its musical properties. LeStrange (2018) chose to record this piece with only the cantus firmus line bowed and the rest of the parts plucked to highlight the onsets and the proportions between the voices.(30) As Loren Ludwig, a fellow music scholar and colleague in LeStrange, has described, his favorite part of playing this piece is the experience of his line having both duple and triple “partners” to feel the rhythm against.
[7.6] The technique of serialized rhythm differs from dispersed meter in several important ways. First, because each part has only a single, distinct note value, displacement of the kind we have modeled to this point is not possible. One could, for example, imagine a version of the Picforth where the entrances of the voices were staggered differently such that there would be no onsets in which all five voices participated. This, however, would weaken the piece as a musical proof of proportional equivalence, which I have argued is its point. Secondly, there are only two meters proposed here: one with a semibreve tactus, and one with a dotted semibreve tactus. Thus, it is not difficult to hear a composite polyrhythm and make sense of the way the voices relate to each other. Lastly, because the effect is unchanging, both listeners and performers have a long time to sit with the rhythmic interplay and to listen from different metrical vantage points. The Picforth allows for a multiplicity of hearings, but it is essentially legible from the outside. Dispersed meter episodes, on the other hand, which have three to five simultaneously expressed meters and last only a dozen seconds or so, are far more resistant to a composite understanding. If the Picforth resembles distributed cognition in its additive creation of meter, so too does dispersed meter, except the result is the additive deconstruction of composite meter.
8. Dispersed Meter
Example 33. Osbert Parsley Spes Nostra,
(click to enlarge and listen)
[8.1] Perhaps the most extraordinary example of dispersed meter in this repertoire comes at the end of Osbert Parsley’s Spes Nostra, which, like many of these examples, is preserved uniquely in GB-Lbl Add. MS 31390. In addition to the episode of dispersed meter at the end of the piece, Parsley sets the cantus firmus in a length of five minims (notated as a breve plus a minim) throughout. Setting the cantus firmus notes in odd lengths is a strategy for variety that Morley recommends, and a length of five minims is the most common non-standard length. Unlike Christopher Tye’s In Nomine Trust, which also sets the cantus firmus in five minims and uses unusually frequent cadences to project five-based groupings,(31) Parsley rarely gives metrical weight to the cantus firmus’s groupings. Yet, having the cantus firmus in five means that in the dispersed meter episode during the final passage of the piece, none of the five voices participate in shared and aligned groupings. As you can see in Example 33, in addition to the cantus firmus’s groups of five, voices two, four, and five are regrouped into ternary units and are displaced from each other in a fully saturated texture. While the top line is largely grouped in breves, the material in measures 71–74 can be interpreted either as a binary syncopation or as two ternary dotted breve groupings.
[8.2] In this texture, every vertical minim initiates a grouping in one voice and sometimes two, but never more. Despite these irregular coincidences, one would be hard-pressed to identify a single, global meter. The fast composite pulse of minims is quite strong, yet to hierarchize them would require privileging one part over another. Some listeners’ ears may gravitate to a particular line or may “try out” several metrical hearings. Performers, of course, will privilege the groupings found within their own part. The musical effect is of a vast space opening up, where the music is suspended from metrical expectations, like a much expanded cadential hemiola. This episode is nearly impenetrable from the outside; a listener would need to choose one of the parts to follow while ignoring the others to have a stable sense of meter. As a result of this metrical chaos, all sense of perceptible meter for an outside listener is obliterated. This produces a very different effect than the Picforth, where the static polymetric texture allows an outside listener to hear a compelling composite meter or to flip between hearing the two primary metrical organizations.
[8.3] This is a good moment to remember that an “outside listener” or “score reader” perspective is not the primary concern of this music and that an inside listener will not feel metrically adrift during this episode. They may feel metrically alone, but not adrift. It is not even a particularly tricky passage to execute. The absolute consistency of the minim onsets in the composite texture serves as an ensemble metronome; it is only the hierarchical organization of those minims that is in disagreement. And yet, there are, temporarily at least, five projected, interlocking metrical environments. Which raises a further question: why look only at the note values? Rhythm and meter can be projected by harmony too. Although speaking of “harmonic rhythm” is usually not particularly fruitful in this repertory, because the passage is completely consonant, the ear is drawn towards moments where the vertical collection of pitches changes. Towards the end of the dispersed meter passage in the Parsley, halfway through measure 75, the rate of vertical change, which had previously been erratic (with changes sometimes arriving two minims in a row), normalizes to the semibreve. This subtle reexpression of the original tactus reorients the listener and the performers as the end of the piece approaches and the voices reconverge.
[8.4] Reminiscent of the end of the Parsley, London describes a kind of metrical unmooring in which “too many notes” at one metrical level make it difficult for the listener to parse the entire metrical structure; what he terms an “overdetermined rhythmic surface” (2012, 17). In a fully saturated displaced texture, however, it isn’t too many notes in any one part that prevent the listener from grasping the metrical structure, but rather too many strong beats projected by the composite texture. Rather than rhythmically overdetermined, the episode in Parsley’s Spes Nostra is metrically overdetermined, or metrically oversaturated. A composite string of minims, each emphasized by a different part or pair of parts, resists hierarchy or the projection of a single metrical structure. From an outside perspective, the goal of this oversaturation of strong beats seems to be a disruption of meter altogether. From a first-person perspective, however, the experience of collective, synchronous meter and individual, competing meters feels quite different. I have come to believe that one of the goals of these passages is to guide performers through the metrical choreography of leaving a shared metrical state for individual ones and then returning to a shared meter.
[8.5] Elizabethen poetry, too, can be said to employ overdetermination to an extent— though poetry, being a single voice, cannot create the dispersed meter effect. William Shakespeare makes use of this technique in Sonnet 116 “Let me not to the marriage of true minds” (1974). When line nine begins, “Love’s not Time’s fool,” Shakespeare alters the basic iambic meter with four stressed syllables in a row. The iamb, a metrical foot made up of an unstressed syllable followed by a stressed one—which also governs the overall meter of the poem—acts as the conceptual figure for Time while the two spondees (stressed-stressed) in a row express Love’s unchangeable nature. The spondees of “Love’s not Time’s fool” break or stop the prevailing meter of the poem, illustrating Time’s inconstancy (unlike Love, the poem asserts). The adjacent spondaic feet produce an oversaturation of stresses, which temporarily dissolve the metrical hierarchy and create a sense of timelessness—and in this case, supply a meaning that amplifies that of the text. Dowland’s song text “Time stands still with gazing on her face” likewise briefly stops time with three accented syllables in a row (1603). The effect works equally well in language and music.
9. Conclusion
[9.1] Dispersed meter—which involves taking a single prevailing metrical organization and breaking it apart into multiple competing metrical realities—is a highly specific effect that Elizabethan composers enjoyed including in their pieces. The component techniques of regrouping and displacement are ones with deep ties to Elizabethan music pedagogical practices as well as to the long established and respected study of proportions in speculative music theory. Accordingly, short instances of regrouping and displacement are widely found in Elizabethan music, with dispersed meter itself representing only their most extreme form. It is unsurprising, then, that occurrences of dispersed meter are found in manuscripts that contain inward-facing repertories (like In Nomines), manuscripts that likely document musicians composing for each other and themselves. Just as the juxtaposition of polyphony and homophony can heighten the pleasures of each melodic texture, moments of dispersed meter act as a sort of metrical polyphony in contrast to the more usual shared metrically homophonic texture.
[9.2] There are many reasons why the dispersed meter effect may have been appealing to Elizabethan composers, but I want to highlight four that I think are most important. First, dispersed meter is virtuosic from a compositional perspective, showing off mastery of counterpoint and dissonance control. Without modern notational and playback technology, writing music like this by hand requires an impressive command of proportions and sense of timespan. This is likely one of the reasons these episodes are usually found within pieces with a cantus firmus: that line acts as a measuring stick for the others, allowing composers to have a frame of reference for the consonances. Second, dispersed meter episodes are virtuosic from a performative perspective, creating a challenge for fellow musicians to navigate. As demonstrated above, the individual musical parts are not usually overly difficult in isolation. Nevertheless, for a successful performance, they require musicians to possess a formidable level of rhythmic accuracy and metrical independence. As the annotations in the Parsons and the marginal rhymes written in Baldwin’s Commonplace Book attest, playing this music was as tricky a task for sixteenth-century musicians as it is for us. For example, Christopher Tye’s formidable proportion piece Sit Fast is followed by the couplet “Singe ye trew & care not:— /for I am trew feare not:—” (GB-Lbl R.M.24.d.2, f. 115r). An earlier anonymous piece advertises, “I am true: then trie mee:— /but singe true: or shame mee:—“ (GB-Lbl R.M.24.d.2, f. 111r). Both rhymes hint not only at the difficulty of the pieces but at the satisfaction of successfully navigating such difficult moments.
[9.3] Third, and most importantly in my opinion, dispersed meter scripts a pleasurable interaction for performers who get to experience both the agential independence of individual metrical realities as well as the satisfaction of reconvening as an ensemble. In this way, dispersed meter functions similarly to an extended complex hemiola, where the prevailing sense of meter is temporarily suspended before finally landing back at a congruence. Analyzing such episodes from a first-person or partbook perspective prioritizes the internally rational metrical organizations of each part over the metrical chaos of the composite. The experience of playing these passages is of musical isolation, you momentarily listen less to your colleagues and more to your inner metronome, hoping that you’ll emerge from the passage together, triumphant. Lastly, dispersed meter creates a profound musical effect for both performers and outside listeners. It suspends global metrical projections to immerse one in a wash of consonance and spatialized rhythmic interplay. The metaphor of “breaking time” for these kinds of passages seems to be one that Elizabethans would have recognized since a similar effect is used in poetry.
[9.4] Whatever their motivations, the effect of timelessness created by metrical dispersion can only exist in dialogue with metrical expectations. Expectation is a prerequisite for disruption and disruption ultimately reinforces the strength of meter through its temporary absence. Yet, this expectation of metrical stability is tempered by the fact that metrical structures in this repertory are also largely emergent rather than predetermined. Performers adept at this repertoire can skim across the rhythmic surface, carving out metrical shapes through grouping choices, some of larger consequence, others of minor detail. If, as I have argued, the main goal of episodes of dispersed meter is the disruption of a composite metrical environment, it follows that outside these moments, Elizabethan composers presupposed a fairly stable set of metrical expectations—more malleable perhaps than later music, but present nonetheless. That moments of dispersed meter are treated so similarly by different composers points to them being deliberately and meaningfully different from the norms of polyphonic composition.
[9.5] Those compositional norms include many clear metrical cues that orient both readers and listeners. Despite the frequent small metrical irregularities, normative Renaissance polyphony contains a strong web of metrical information, including note lengths, melodic shape, and characteristic contrapuntal figures. Indeed, the very rules of counterpoint and dissonance treatment are predicated on the metrical weight of different note values and initia. In most cases, the irregularities themselves ultimately reinforce the sense of meter. From the outside, dispersed meter episodes differ from these norms: instead of reinforcing meter, they remove the contrapuntal metrical information (dissonances) and overwhelm the ear with metrical onsets to erase the sense of global meter. The listener may allow their ears to wander from part to part, focusing in on one line at a time and following the metrical implications of it, but the total sound is metrically chaotic. Yet within the metrical chaos, the “inside” experience of the performers is one of straightforward individual lines of polyphony, each asserting a single, largely uncomplicated metrical organization. The result: a centrifugal composite made of centripetal parts.
[9.6] If we adopt a different set of analytical values, one that privileges the individual lines and the interactions of the musicians over an outside listener, perhaps there’s no longer any incentive to try to parse the composite. Instead, we can see these passages instantiating the social relationships of the musical ensemble: a movement from metrical unity to metrical dispersion and back as the voices break apart and assert their individual freedom from each other before satisfyingly reconvening at the end of the episode. Looking at Elizabethan polyphony this way not only honors the social contexts and uses of this music, it also invites us to develop a more pluralistic view of metrical experience and analysis. Even in passages that might easily be analyzed compositely from the outside, individual parts may still present distinct metrical affordances, and the metrical interactions between the musicians may offer new paradigms for understanding meter.
Zoe Tall Weiss
Lamont School of Music
University of Denver
2344 E Iliff Ave
Denver, CO 80210
Zoe.Weiss@du.edu
Works Cited
Boone, Graeme M. 2000. “Marking Mensural Time.” Music Theory Spectrum 22 (1): 1–43. https://doi.org/10.2307/745851.
Bray, Roger. 1995. “Music and the Quadrivium in Early Tudor England.” Music & Letters 76 (1): 1–18. https://doi.org/10.1093/ml/76.1.1.
Busse Berger, Anna Maria. 1993. Mensuration and Proportion Signs: Origins and Evolution. Oxford University Press. https://doi.org/10.1093/oso/9780198162308.001.0001.
Butler, Charles. 1636. The Principles of Musik, in Singing and Setting With the Two-Fold Use Thereof, Ecclesiasticall and Civil. Printed by John Haviland, for the author.
Butler, Katherine. 2019. “From Liturgy and the Education of Choirboys to Protestant Domestic Music-Making: The History of the ‘Hamond’ Partbooks (GB-Lbl: Add. MSS 30480-4).” Royal Musical Association Research Chronicle 50 (1): 29–93. https://doi.org/10.1080/14723808.2018.1546477.
Cohn, Richard. 2001. “Complex Hemiolas, Ski-Hill Graphs and Metric Spaces.” Music Analysis 20 (3): 295–326. https://doi.org/10.1111/1468-2249.00141.
—————. 2016. “A Platonic Model of Funky Rhythms.” Music Theory Online 22 (2). https://doi.org/10.30535/mto.22.2.1.
—————. 2020. “Meter.” In The Oxford Handbook of Critical Concepts in Music Theory, ed. Alexander Rehding and Steven Rings, 207–33. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190454746.013.9.
Collins, Denis. 2007. “‘Sufficient to Quench the Thirst of the Most Insaciate Scholler Whatsoeuer’: George Waterhouse’s 1.163 Canons on the Plainsong Miserere.” In Canons and Canonic Techniques, 14th-16th Centuries: Theory, Practice, and Reception History, ed. Katelijne Schiltz and Bonnie J. Blackburn, 407–20. Peeters. https://doi.org/10.2307/jj.22992789.28.
Danner, Peter Kolb. 1967. “The ‘Miserere Mihi’ and the English Reformation: A Study of the Evolution of a ‘Cantus Firmus’ Genre in Tudor Music.” PhD diss., Stanford University.
DeFord, Ruth I. 2015. Tactus, Mensuration and Rhythm in Renaissance Music. Cambridge University Press. https://doi.org/10.1017/CBO9781107587717.
Dowland, John. 1603. The Third and Last Booke of Songs or Aires. Printed by P.S[hort], for Thomas Adams.
Dumitrescu, Theodor. 2007. The Early Tudor Court and International Musical Relations. Ashgate.
Dygon, John. 2006. John Dygon’s Proportiones Practicabiles Secundum Gaffurium. Translated by Theodor Dumitrescu. University of Illinois Press.
Edwards, Warwick. 1970. “The Performance of Ensemble Music in Elizabethan England.” Proceedings of the Royal Musical Association 97: 113–23. https://doi.org/10.1093/jrma/97.1.113.
—————. 1978. “The Instrumental Music of Henry VIII’s Manuscript.” The Consort: Annual Journal of the Dolmetsch Foundation 34: 274–82.
—————. 2013. “Songs without Words by Josquin and His Contemporaries.” In Secular Renaissance Music: Forms and Functions, ed. Sean Gallagher, 575–88. Ashgate.
Fallows, David. 1996. “The End of the Ars Subtilior.” Basler Jahrbuch Für Historische Musikpraxis 20: 21–40.
Fellowes, Edmund H. 1948. The English Madrigal Composers. Oxford University Press.
Flynn, Jane Elizabeth. 1993. “A Reconsideration of the Mulliner Book (British Library Add. MS 30513): Music Education in Sixteenth-Century England.” PhD diss., Duke University.
—————. 1995. “The Education of Choristers in England during the Sixteenth Century.” In English Choral Practice (1400–1650): A Memorial Volume to Peter Le Huray, ed. John Morehen, 180–99. Cambridge University Press. https://doi.org/10.1017/CBO9780511552410.010.
Gaffurius, Franchinus. 1993. The Theory of Music. Translated by Walter Kurt Kreyszig. Yale University Press.
Glareanus, Henricus. 1965. Dodecachordon. Translated by Clement A. Miller. American Institute of Musicology.
Gombosi, Otto. 1952. Review of Jacobus Vaet and His Motets, by Milton Steinhardt. The Musical Quarterly 38 (1): 159–67. https://doi.org/10.1093/mq/XXXVIII.1.159.
Grant, Roger Mathew. 2014. Beating Time & Measuring Music in the Early Modern Era. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199367283.001.0001.
Hasty, Christopher Francis. 2020. Meter as Rhythm: 20th Anniversary Edition. Oxford University Press. https://doi.org/10.1093/oso/9780190886912.001.0001.
Hatter, Jane D. 2019. Composing Community in Late Medieval Music: Self-Reference, Pedagogy, and Practice. Cambridge University Press. https://doi.org/10.1017/9781108643597.
Heminger, Anne. 2018. “Music Theory at Work: The Eton Choirbook, Rhythmic Proportions and Musical Networks in Sixteenth-Century England.” Early Music History 37: 141–82. https://doi.org/10.1017/S0261127918000074.
Klorman, Edward. 2016. Mozart’s Music of Friends: Social Interplay in the Chamber Works. Cambridge University Press. https://doi.org/10.1017/CBO9781316145302.
Kolb, Paul. 2017. “Divisions of Dots and Dots of Division: History, Theory, and Practice.” Tijdschrift van de Koninklijke Vereniging voor Nederlandse Muziekgeschiedenis 67 (1/2): 177–90.
Kozak, Mariusz. 2020. Enacting Musical Time: The Bodily Experience of New Music. Oxford University Press. https://doi.org/10.1093/oso/9780190080204.001.0001.
—————. 2021. “Feeling Meter: Kinesthetic Knowledge and the Case of Recent Progressive Metal.” Journal of Music Theory 65 (2): 185–237. https://doi.org/10.1215/00222909-9143190.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195116236.001.0001.
Lerdahl, Fred, and Ray S. Jackendoff. 1983. A Generative Theory of Tonal Music. The MIT Press. https://doi.org/10.7551/mitpress/12513.001.0001.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001.
Long, Megan Kaes. 2020. Hearing Homophony: Tonal Expectation at the Turn of the Seventeenth Century. Oxford University Press. https://doi.org/10.1093/oso/9780190851903.001.0001.
Ludwig, Loren Monte. 2011. “‘Equal to All Alike’: A Cultural History of the Viol Consort in England, c.1550–1675.” PhD diss., University of Virginia.
Malinowski, Stephen. “Music Animation Machine.” www.musanim.com. Accessed October 22, 2025.
McGuinness, David. 1994. “Syncopation in English Music, 1530–1630: ‘Gentle Daintie Sweet Accentings’ and ‘Unreasonable Odd Cratchets.’” PhD diss., University of Glasgow.
Miller, Hugh M. 1947. “Pretty Wayes: For Young Beginners to Looke On.” The Musical Quarterly 33 (4): 543–56. https://doi.org/10.1093/mq/XXXIII.4.543.
Milsom, John. 2005. “Crecquillon, Clemens, and Four-Voice Fuga.” In Beyond Contemporary Fame: Reassessing the Art of Clemens Non Papa and Thomas Crecquillon, 293–346. Brepols.
—————. 2016. “Cipriano’s Flexed Fuga.” In Cipriano de Rore: New Perspectives on His Life and Music, ed. Jessie Ann Owens and Katelijne Schiltz, 293–330. Brepols.
Morley, Thomas. 1597. A Plaine and Easie Introduction to Practicall Musicke. Peter Short, dwelling on Breedstreet hill at the signe of the Starre.
Ovenden, Philippa. 2023. “Out of the Blue: Preparing Proportions in the Old Hall Manuscript.” Music Theory Online 29 (4). https://doi.org/10.30535/mto.29.4.4.
Owens, Jessie Ann. 1998. Composers at Work: The Craft of Musical Composition 1450–1600. Oxford University Press. https://doi.org/10.1093/oso/9780195095777.001.0001.
Rastall, Richard. 1997. “Spatial Effects in English Instrumental Consort Music, c.1560–1605.” Early Music 25 (2): 269–89. https://doi.org/10.1093/earlyj/XXV.2.269.
—————. 2022. “Spatial Dispositions in English Instrumental Consort Music, c.1575–1650: A Further Examination.” Early Music 50 (1): 51–64. https://doi.org/10.1093/em/caab081.
Rodin, Jesse. 2024. The Art of Counterpoint from Du Fay to Josquin. Cambridge University Press. https://doi.org/10.1017/9781316882191.
Shakespeare, William. 1974. The Riverside Shakespeare. 6th printing, with Corrections and Additions. Houghton Mifflin.
Stoessel, Jason. 2009. “The Interpretation of Unusual Mensuration Signs in the Notation of the ‘Ars Subtilior.’” In A Late Medieval Songbook and Its Context: New Perspectives on Codex Chantilly (Bibliothèque Du Château de Chantilly, Ms. 564), ed. Yolanda Plumley and Anne Stone, 179–202. Brepols. https://doi.org/10.1484/M.EM-EB.3.2666.
—————. 2010. “Looking Back over the ‘Missa L’Ardant Desir’: Double Signatures and Unusual Signs in Sources of Fifteenth-Century Music.” Music & Letters 91 (3): 311–42. https://doi.org/10.1093/ml/gcq059.
van Orden, Kate. 2015. Materialities: Books, Readers, and the Chanson in Sixteenth-Century Europe. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199360642.001.0001.
Weiss, Zoe Tall. 2020. “The Merry Jests of Jenkins’s Partbooks.” Journal of the Viola Da Gamba Society of America 51: 5–26.
—————. 2021. “The Sixteenth-Century In Nomine: Networks of Mobility, Influence, and Intertextuality.” PhD diss., Cornell University.
Witek, Maria A.G. 2017. “Filling in: Syncopation, Pleasure and Distributed Embodiment in Groove.” Edited by Kenneth M. Smith. Special Issue on Popular Music, Music Analysis 36 (1): 138–60. https://doi.org/10.1111/musa.12082.
Zazulia, Emily. 2021. Where Sight Meets Sound: The Poetics of Late Medieval Music Writing. Oxford University Press. https://doi.org/10.1093/oso/9780197551912.001.0001.
Discography
Discography
Fretwork. 2019. In Nomine II. Signum Classics.
LeStrange Viols. 2018. Æternum: Music of the Elizabethan Avant Garde from Add. MS 31390. Olde Focus Recordings.
Phantasm. 2014. Four Temperaments. Linn Records.
The Spirit of Gambo. 2014. Christopher Tye: Consort Music – In Nomine. Musica Ficta.
Footnotes
* This article has benefitted from the insights and suggestions of many readers, including Megan Kaes Long and the anonymous reviewer for MTO, Jonathan Leathwood, David H. Miller, and the University of Denver Musicology/Ethnomusicology/Theory writing group. I offer my deepest gratitude to Mitch Ohriner, who read multiple drafts and whose ideas have much improved my thinking. Thanks also to Ross Duffin for allowing me to use his beautiful Ravenscroft font for the mensuration symbols.
Return to text
1. See Butler 2019 for a comprehensive history of the Hamond Partbooks (GB-Lbl Add. MS 30480–4). She locates Robert Parsons’s Ut re mi fa as having been copied during Phase VI, when the partbooks were being used for domestic music making by the Hamond family and blank pages from its earlier life in a pedagogical context were being infilled. See Hatter 2019 for pieces built on the hexachord and other kinds of “music about music.”
Return to text
2. The hexachord was not itself a scale but a theoretical understanding of pitch space that aided in sight singing and reading music. The six syllables define five intervals: whole step, whole step, half step, whole step, whole step. There were three standard hexachords (starting on C, F, and G) but through transposition one could create others as well. When reading music, one “mutates” between different hexachords to accommodate the range of a part and the need for more than one half step.
Return to text
3. Throughout this article, I will refer to note values using the Latinate naming conventions of sixteenth-century English music theorists: breve (double whole note), semibreve (whole note), minim (half note), and semiminim (quarter note). Transcriptions preserve the original note values unless otherwise noted.
Return to text
4. Butler (2019) suggests that errors/corruptions in the copying of the partbooks are responsible for the difficulty alluded to in the textual notes. However, the fact that these textual notes appear only in the altus and bassus partbooks and not the tenor—whose part, while rhythmically identical is aligned with the cantus firmus—convinces me that they refer to this difficult passage where the altus and bassus must both depart from the established tactus and reorganize their internal metrical projection.
Return to text
5. The practice of writing stress-reversed imitative entries illustrates just one of the ways that Renaissance music departs from Lerdahl and Jackendoff’s (1983) metrical preference rules (MPR) where they rank parallelism as a primary metrical consideration.
Return to text
6. The six-part Anonymous In Nomine in GB-Lbl Add. MS 31390 is an interesting exception. The cantus firmus notes are the length of a dotted breve but are notated as two dotted semibreves per pitch, implying a compound duple meter. The non-cantus firmus voices are very clearly in a simple triple meter throughout the entire piece, including moments of unusual homophony.
Return to text
7. Cohn’s (2020, 210) own proposed definition of meter avoids perception, abstracting the concept to “an inclusionally related set of distinct, notionally isochronous time-point sets.” This definition differs from others in its requirement that meter go beyond simple entrainment to a single isochronous pulse without differentiation, hierarchy, or subdivision. Cohn requires the interaction of at least two (mostly) isochronous pulses to form a hierarchized sense of meter. This arithmetical approach means that while periodicity is not necessarily a requirement, it seems to be an assumption—Cohn’s discussion of irregularity in meter occurs within the context of repeated cyclical patterns. In focusing on the hyper-locality of moment-to-moment metrical projections, Hasty’s preference for linearity rather than cyclicity is useful for Renaissance music.
Return to text
8. In Renaissance music, cadences to A are often ambiguous as to whether they should be interpreted as Phrygian cadences with the B altered to
Return to text
9. Despite being textless, these pieces are not necessarily “instrumental.” There are few, if any, consistent distinctions in Elizabethan music between works intended for vocal or instrumental performance (Edwards 2013 and 1970). Some Continental works set originally with words circulated exclusively without text in England, and the singing of untexted pieces on solmization syllables was common practice. The title page of the table book GB-Lbl Add. MS 31390 (which contains many of the pieces discussed here and is untexted) declares that it is “A booke of In nomines & other solfainge songes of v:vi:vii:&viii pts for voyces or Instruments.” Nevertheless, there are some compositional techniques that are more prevalent in untexted polyphony than in texted works, specifically sequences, ostinatos, fragmented disjunct motives (resembling arpeggios), and dispersed meter episodes (Edwards 1978, Weiss 2021).
Return to text
10. See Ludwig 2011 and Weiss 2021 for the social and cultural context of In Nomines and other textless polyphony in England.
Return to text
11. Thomas Morley, who received his musical education after the Elizabethan Settlement and studied with William Byrd, for example, devotes an entire third of his Plaine and Easie Introduction to Practicall Musicke (1597) to the techniques of descanting and writing canons over a plainsong.
Return to text
12. Rodin (2024) also makes an argument for non-blend as a musical value of this period.
Return to text
13. The category of pieces titled “In Nomine,” which are all built on a cantus firmus derived from a mass movement by John Taverner, some which contain episodes of dispersed meter, are highly intertextual, speaking to the community’s familiarity with this repertoire and the musical instantiations of different kinds of relationships among its members: students and teachers, colleagues, rivals (Weiss 2021).
Return to text
14. Induction is well explained and documented in Dumitrescu 2007. Ovenden (2023) discusses additional types of preparation that facilitate the performance of complex proportional relationships.
Return to text
15. Giles received a BMus from Oxford in 1585 and eventually a doctorate in 1622, so he was well versed in academic music. Though the date of the piece is given as 1594 in the manuscript, at least the last line of the inscription must have been added later, as he wasn’t appointed Gentleman and Master of the Children of the Chapel Royal until 1597 (though he kept his Windsor appointment simultaneously).
Return to text
16. I encourage readers to try out this series of rhythmic transformations with a metronome serving as your cantus firmus. The faster the metronome, the easier the proportions, but a frenzied flourish of 9:1 at the end of the piece suggests to me that 60bpm is probably the upper limit for the cantus firmus. Presumably, early modern musicians were indeed able to accomplish these difficult rhythmic feats. Morley offers an anecdote about this: “another descanter, a companion of my master’s, who never came in my master’s company…but they fell to contention, striving who should bring in the point soonest and make hardest Proportions, so that they thought they had won great glory if they had brought in a point sooner or sung harder Proportions the one than the other” (1597, 120).
Return to text
17. While the performance context for untexted polyphony shifted towards domestic viol playing among upper class amateurs in the early-seventeenth century, this was also an insular context (Butler 2019; Ludwig 2011).
Return to text
18. Kozak explains his choice to focus solely on the temporal experience of listeners by stating that in the literature on embodiment in music, “There is a lot more focus on the performers’ bodies in relation to musical meaning” (pg 7, footnote 5).
Return to text
19. In earlier repertories where note lengths themselves are more contextual (and may require imperfection or alteration), readers also must scan ahead and read both forwards and backwards.
Return to text
20. Listening to a recording of a piece you know well perhaps allows for a similar sort of expectational duality of metrical experience: the body is waiting and ready to make the metrical shift.
Return to text
21. This assumes that slurring across significant metrical groupings was not an unnotated norm of sixteenth-century viol playing. While there is evidence that unnotated slurs may have been used, later patterns of extant slurring suggest these slurs would likely not have crossed metrical boundaries.
Return to text
22. Edward Klorman (2016) has discussed the way players of individual parts may feel a sense of agency over the musical actions their part takes. Though Klorman’s discussion is in the context of late-eighteenth century chamber music, it remains relevant to the equally social and even more democratic textures of imitative polyphony.
Return to text
23. Flynn (1993) argues that these rhythmicization patterns are examples of “figuration” which she documents as a skill called for in chorister curricula.
Return to text
24. Butler copies frequently from Morley, though he usually provides attribution (McGuinness 1994, 103).
Return to text
25. See Zazulia 2021 and Stoessel 2009 for more on intrinsic and extrinsic notation.
Return to text
26. Particularly in the case of Tye, it is worth considering that the manuscript copies (including GB-Lbl Add. MS 31390, which includes unica of many of Tye’s twenty-one In Nomine settings), are posthumous and might postdate composition by as much as two or three decades. It is entirely possible that Tye’s original notation used more mensural proportion signs but was translated into the newer conventions of notation, which preferred the quasi-fixed note values of the ubiquitous cut-C. Some evidence of this translation can be seen in the inconsistent and varied use of mensuration symbols: three different notations are used to indicate the sesquitertia proportion here.
Return to text
27. Cohn (2020) has argued for the equivalence of these concepts and suggested that Krebs’s (1999) “grouping dissonances” should be understood as proportional metric substitutions under the umbrella category of “hemiolas.” While conceptually sound, Cohn’s use of the term “hemiola” as a category is a decidedly awkward fit for this repertory. In the Renaissance, “hemiola” refers to the specific proportion of sesquialtera (3:2), thus using it for the entire category of proportions or proportional substitutions is too imprecise a use of synecdoche. In fact, the most common proportion created by regrouping in this repertory is sesquitertia (4:3). The term hemiola comes from the Greek ἡμιόλιος and is used interchangeably in music theoretical treatises with the Latin term sesquialtera. In addition to describing rhythmic proportions, both terms are used frequently to describe the harmonic interval of the perfect fifth, also defined by the 3:2 ratio. As Gaffurius explains: “They [i.e. the above-named writers [Macrobius, Boethius, etc.]] suppose that ‘hemiolic’ is derived from ‘hemi,’ meaning half, and ‘olon,’ whole; that is, a whole and a half. ‘Sesquialter’ is appropriately derived from ‘sesqui,’ which is the half (as Cola Montanus had it) and from ‘alter,’ since a part equal to half the other number is added to the integer. This proportion itself is the hemiolia or the sesquialter.” (Gaffurius 1993, 116). Morley discusses the term hemiola only to chide those who misuse it to describe tripla proportions in music, writing, “for Hemiola doth signifie that which the Latines tearme
Return to text
28. Stoessel (2010) discusses a similar phenomenon of proportional mensuration signs that refer successively to each other, rather than to some global mensural framework.
Return to text
29. I am indebted to Loren Ludwig for sharing some of these examples with me.
Return to text
30. LeStrange also transposed the piece down a fourth to D (the most common key for In Nomines) to take best advantage of the resonance of the plucked strings. Other ensembles have since copied our use of pizzicato for this piece but without the transposition, which I find less successful. Pizzicato as a technique on the viol is documented in the early-seventeenth century works of Tobias Hume.
Return to text
31. The fact that Tye feels the need to mark so many of the groups of five with cadences reinforces the metrical weakness of the cantus firmus.
Return to text
Copyright Statement
Copyright © 2025 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Andrew Eason, Senior Editorial Assistant
Number of visits:
1226