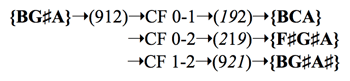Models and Music Theory: Reconsidering David Lewin’s Graph of the 3-2 Cohn Cycle
Michael Fitzpatrick
REFERENCE: http://www.mtosmt.org/issues/mto.07.13.4/mto.07.13.4.reed_bain.html
REFERENCE: http://www.mtosmt.org/issues/mto.07.13.3/mto.07.13.3.nolan.html
KEYWORDS: Cohn functions, Cohn cycles, Iconic models, David Lewin, Reed and Bain
ABSTRACT: Iconic models are ubiquitous in music theoretical literature. Their purpose is to illustrate and thereby concretize abstract theoretical concepts that would otherwise exist only in the imagination. Despite the prevalence of iconic models, we find few comprehensive analyses of how they serve this purpose and the conceptual mechanisms that relate models to their subjects.
This commentary is a case study that compares two competing music theory models and raises some of the questions that arise when evaluating a particular model’s fit with its theoretical subject. Here, I examine Reed and Bain’s assertion that their Tonnetz design provides a more satisfactory depiction of the sc 3-2 Cohn cycle than David Lewin’s graphic network of the same. By relating the iconic components of each model with elements of the theory, I suggest that Lewin’s network corresponds more accurately to the sc 3-2 Cohn cycle than Reed and Bain’s Tonnetz.
Copyright © 2011 Society for Music Theory
Introduction
[1] In a recent issue of this journal, Jacob Reed and Matthew Bain (2007) review David Lewin’s (1996, 1998) graphic network of the set-class (sc) 3-2 Cohn cycle and his analysis of J. S. Bach’s F-sharp Minor Fugue, WTC I. Exploring different modeling options, Reed and Bain reformulate Lewin’s “Graph” into a Tonnetz, per Cohn 1997. After a brief consideration of the Tonnetz, however, Reed and Bain reject this model and Lewin’s graph as inappropriate candidates for visualizing the transformations of the instantiations of sc 3-2 in the exposition of Bach’s fugue. Since these two-dimensional models exist in pitch-class (pc) space they are unequipped to solve “the problems of register, pitch-specific structure and order” (Reed and Bain 2007, [1.6]) in the unfolding fugal process. Finally, Reed and Bain present an animated three-dimensional tetrahelix as a solution to this modeling problem. Inasmuch as their tetrahelix is crafted specifically for the purpose of animating Bach’s fugue, Reed and Bain’s final result successfully integrates our imagination of the music progressing through pitch-space and time with a visual representation of that imagined motion.
[2] The authors’ comparison of Lewin’s graph and their Tonnetz raises some questions concerning the relationship between music theory models and their subjects, the theoretical concepts that they illustrate. We may say generally that music theory models render observable abstract theoretical concepts that would otherwise remain in the imagination. They accomplish this by depicting abstract theoretical relations with an enduring and visible iconic design.(1) Lewin’s graph and the Tonnetz are examples of iconic models; both use visual imagery to depict concretely an abstract theoretical Cohn cycle. Such iconic models pervade music theory literature, especially that of neo-Riemannian and transformational theory.
[3] Reed and Bain argue that the Tonnetz representation of the 3-2 Cohn cycle, even though ultimately inadequate for their purposes, is a more satisfactory and economical model of the theory than Lewin’s graph.(2) Here, I would like to consider—albeit indirectly—the larger question of the relationship between music theory models and their subjects by using as a case study Reed and Bain’s arguments in favor of their Tonnetz. I suggest alternatively that Lewin’s original graph is more successful than the Tonnetz in depicting the theoretical concept of a Cohn cycle as Lewin 1996 describes.(3) I shall do this by examining and answering each of Reed and Bain’s criticisms of Lewin’s graph and by considering the perceived solutions that the Tonnetz offers with a particular focus on how the iconic components of each model relate to the theory of Cohn cycles. Unduly privileging a personal taste for visual aesthetics over a more rigorous modeling of the theory, Reed and Bain’s Tonnetz relates to its subject less clearly and directly than Lewin’s graph. I begin with brief analyses of the two models.
Lewin’s Graph
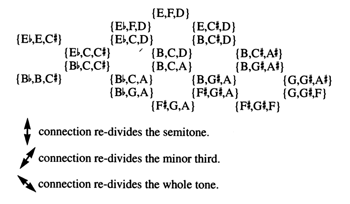
[4] Lewin’s two graphic presentations of the 3-2 Cohn cycle are reproduced below. Figure 1 is the original model that appears in “Cohn Functions” (Lewin 1996); Figure 2 is an expanded version of the same model that Lewin uses for his analysis in “Notes on the Opening of the
|
Figure 1. Lewin 1996 (click to enlarge) |
Figure 2. Lewin 1998 (click to enlarge) |
Lewin’s graph is a network of trichordal nodes interconnected by vertical and diagonal axes.(5) Each node represents a particular unordered pc instantiation of sc 3-2; each axis corresponds to one of the three possible Cohn flips of the Cohn function derived from the successive-interval array (sia) of sc 3-2, (129).(6) Therefore, every node is connected to three others by one of the three possible Cohn flips of this Cohn function. Table 1 demonstrates this for pcset {B
Table 1. Note: “CF 0-1” reads “Cohn-flip about arguments 0 and 1,” etc. Cohn-flipped arguments are shown in italics.
(click to enlarge)
[5] Assuming enharmonic equivalence, every trichordal node preserves a common dyad—either a semitone, whole tone, or minor third—with each of its adjacent Cohn-flip-related nodes. Even though this Cohn cycle is generated by Cohn-flipping the Cohn function (129) and not by Cohn-flipping the actual pcs involved, Lewin’s graphic layout reflects his decision to show what he calls “‘modulating’ cycles among prime and inverted forms of the sets” (Lewin 1996, 187). The choice to retain common dyads between the pcsets on the graph creates a highly interconnected network that eventually cycles through all twenty-four distinct forms of the sc. Even though pc is important in Lewin’s representation, it does not play an essential role in generating this Cohn cycle.(7)
[6] In sum, Lewin’s graph renders visible the highly abstract theoretical concepts of Cohn flips, Cohn functions, and Cohn cycles: it is an iconic model whose interaction of nodes and axes illustrate the relationships that the theory describes. It is an efficient representation as well, since every option that any particular pcset has for “modulating” via Cohn flip is exhausted on the network.
Reed and Bain’s Tonnetz
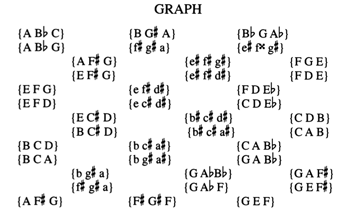
Figure 3. Reed and Bain 2007
(click to enlarge)
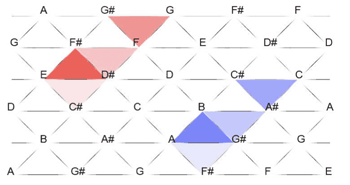
[7] Figure 3 reproduces the Tonnetz that Reed and Bain (2007) construct for the same 3-2 Cohn cycle.(8) Like Lewin’s graph, the Tonnetz is a network of nodes and axes. Each node represents a pc and each axis (the edges of the triangles) represents an interval class (ic): “Moves along the horizontal axes are moves of interval class 1. Moves on the diagonal axes are either ic2 or ic3” (2007, [1.3]). Nodes of pcs joined by axes form triangles that each represent a particular pc instantiation of sc 3-2. Edges shared between adjacent triangles show common dyad retention between them—either a semitone, whole tone, or minor third. Reed and Bain point out that the relationship of any given triangle to one of its three neighbors is by Cohn flip. Therefore, a Cohn flip on the Tonnetz is a dynamic “flipping” of one sc 3-2 triangle around one of its edges to fuse with another. For example, we may take the {B
[8] In sum, Reed and Bain’s Tonnetz model is unmistakably geometrical insofar as its triangles are immediately visual with the axes of the network explicitly drawn. It compresses the information from Lewin’s graph by eliminating the pc duplication between adjacent pcsets and thereby creates an evenly distributed layout. Furthermore, the Tonnetz does not depend on curly braces to show the unordered character of the pcsets, and it exhausts the possible Cohn flip relations between the pcsets in the network.
Comparison of the Models
[9] Reed and Bain (2007, [1.2]) raise three interpretive difficulties concerning the layout and design of Lewin’s graph: first, pc duplications within Lewin’s network “make it difficult to imagine the music progressing through the graph”; second, “the format of staggered rows and columns...arbitrarily prioritizes the Cohn flips that preserve minor seconds”; and third, Lewin’s ordering of the sc 3-2 trichords “so that the common tones of the Cohn-flip-related sets are, for the most part, in the same place...unfortunately rotates the interval content of each set, when read left to right, making the Graph harder to read.” They then discuss how the Tonnetz design removes these perceptual problems.
[10] Regarding the first objection, the problematic nature of the pc duplication seems to stem from Reed and Bain’s personal taste in visual aesthetics, since they admit that the pc duplication is “rendered harmless when the graph is theoretically conceived in pitch-class space” (2007, [1.2]). One wonders, then, why the authors raise this concern as they also point out that Lewin originally conceived his graph of the Cohn cycle within pc space (2007, [1.5]). It seems misplaced to criticize a model with reference to a theoretical concept that it does not mean to illustrate—in this case, pitch-space. This criticism undoubtedly arises from Reed and Bain’s desire to evaluate the model’s capability to animate the order of events in a specific piece of music, namely Bach’s F-sharp Minor Fugue. Reconstructing the model of the 3-2 Cohn cycle may suit their purposes for conceiving the fugal exposition in pitch-space but it does not thereby offer a fair assessment of Lewin’s graph, which models primarily a theoretically conceived Cohn cycle distinct from any individual piece of music. Reed and Bain seem to confuse the purpose of Lewin’s graph as a theoretical model with its potential application in a hypothetical analysis or animation. The pc duplication in Lewin’s model does not adversely affect its relationship to the 3-2 Cohn cycle or its identity as a concrete representation of the same theoretical abstraction. Perhaps, then, the elimination of pc duplication that the Tonnetz design provides should not be counted as a desirable alternative to Lewin’s graph as the authors suggest:
This (013) Tonnetz succeeds in restructuring the trichords as individual pitch classes grouped in a triangular form so that neighboring sets can literally share common tones. The triangulation of trichords provides a more accurate representation of common tone retention between Cohn-flip-related sets (Reed and Bain 2007, [1.3], italics added).
Reed and Bain fail to qualify in what way the Tonnetz design is “more accurate” in this regard. If by this the authors mean that common dyad retention on the Tonnetz is more immediate visually, they could argue this point; but, such a qualification is surely necessary in all fairness to Lewin’s original work.
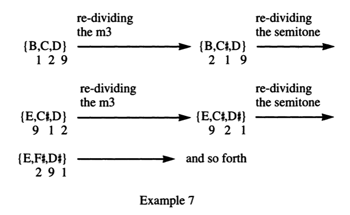
Figure 4. Lewin’s Example 7
(click to enlarge)
[11] Skipping ahead for the moment, Reed and Bain’s third criticism is in similar need of qualification. In their assessment, Lewin’s decision to depict the trichords on the graph so that the common dyads between adjacent pcsets are held in the same order positions (for the most part) is “unfortunate” since it “rotates the interval content of each set, when read left to right, making the Graph harder to read” (2007, [1.2]). This criticism is difficult to understand as they express it. Lewin’s Cohn cycle graph is generated by Cohn-flipping the Cohn function (129) derived from the sia of sc 3-2. Performing any of the three possible Cohn flips on this Cohn function does nothing else than rotate the interval content of each pcset by exchanging the values at the ordered argument positions within the function (see Table 1). I refer back to Lewin’s clear explanation of this from “Cohn Functions,” including his own illustration (“Example 7” in Figure 4):(9)
Clampitt, in his letter, listed exhaustively the many pcset classes that have interval series representable by 3-valued Cohn functions. All trichords whose interval-series have three distinct values are such. Example 7 demonstrates for the interval series (129).
In the example, the first transition corresponds to a Cohn flip of the pcsets involved—C♯ is adjacent to C as a pitch class. But the second transition is not a Cohn flip of pcsets—E is not adjacent to B as a pitch class. Nevertheless the transition is generated by an exchange of distinct adjacent values in the interval series, 2 and 9 being adjacent values for the mod 3 function (219). Indeed any 3-valued function mod 3 is de facto a Cohn function. (xyz), in all generality, Cohn-flips at arguments 0 and 1: (yxz) is a rotated retrograde of (xyz). (xyz) also Cohn-flips at arguments 0 and 2: (zyx) is the retrograde of (xyz). Furthermore, (xyz) also Cohn-flips at arguments 1 and 2: (xzy) is a rotated retrograde of (xyz). (xyz) thus Cohn-flips at three different adjacent-argument pairs (Lewin 1996, 188).
This 3-2 Cohn cycle is generated precisely by rotating the interval content of each adjacent pcset on the graph to form a new pcset within the same sc. This is what defines Lewin’s network as a model of a Cohn cycle as opposed to anything else.
[12] Reed and Bain describe Lewin’s graph as a depiction of “Cohn flips on the pcset (013)” (2007, 1.5). While Lewin’s graph does indeed show a particular set of pc transformations of sc 3-2, Reed and Bain’s characterization here is misleading. Lewin’s prose clearly demonstrates that the Cohn cycle in question does not depend upon Cohn-flipping pcs and any Cohn flip relationships that arise between pcs on the graph are incidental. Instead of showing Cohn flips on pcset (013) as Reed and Bain suggest, Lewin’s graph models Cohn flips of Cohn function (129).(10)
[13] Reed and Bain’s second criticism holds the most potential for an active comparison of the two models. In their assessment, the even and homogeneous Tonnetz design removes the temptation to interpret erroneously the Cohn flip that preserves the minor-second dyad (Lewin’s vertical axis) as somehow more significant than the other two. Of course, Reed and Bain do not contend that Lewin assigns a priority among Cohn flips: a careful reading of “Cohn Functions” prevents such an interpretation. Conceding for the moment, however, that the layout of Lewin’s graph could create this confusion, we can evaluate the solution that the Tonnetz offers. Indeed, there are no spatial “gaps” on the Tonnetz as there are in Lewin’s graph: every Cohn flip on the Tonnetz appears equidistant within its metaphorical space.
Table 2. Cohn Flip Relationships between Two Neighbouring Triangles on the Tonnetz
(click to enlarge)
[14] The Tonnetz leaves each triangular pcset unordered: Reed and Bain do not specify the direction in which to read each triangle around its edges. This layout causes difficulty in relating the Tonnetz, as a model, to the 3-2 Cohn cycle. Because the order in which one may read each triangle is undefined, the particular ordering of that pcset’s sia, or Cohn function, is consequently undefined. For example, taking trichord {FDE} at random from the upper portion of the Tonnetz (see Figure 3) we may read the sia along the edges of the triangle in three different ways: proceeding counterclockwise from pc F, we obtain <9-2-1>; counterclockwise from pc E, <1-9-2>; and counterclockwise again from pc D, <2-1-9>. This interpretive multiplicity renders ambiguous the particular Cohn flip relationship that connects any triangles sharing an edge. Since each triangle may have three different readings of its sia, each triangle may relate to any of its neighbors by a possible nine different Cohn flips of the Cohn function (129). Table 2 illustrates this using pc sets {FDE} and {FD
[15] Cohn flip relationships between adjacent triangles are not as literal as Reed and Bain describe: “In this manner, the entire surface of the Tonnetz can be traversed with rotations over common tone edges—literal Cohn flips” (2007, [1.3]). Using the Tonnetz, one must first decide the order of the sia of a source trichord, and second the specific Cohn flip that transforms it by reading the destination trichord appropriately. In other words, the reader must project particular Cohn flips onto the Tonnetz geometry in order to reveal the Cohn cycle in question. In contrast, Lewin’s graph leaves the sia of each trichord defined in terms of order and thereby indicates clearly the unique Cohn flip that connects adjacent pcsets. Ironically, Reed and Bain have injected a greater degree of complexity into their Tonnetz model even as they aim for a greater simplicity.
[16] Recognizing that the sia of every triangle on the Tonnetz may be interpreted in three different ways presumes one has first noticed that the direction in which the triangles may be read depends on the direction they point. Triangles pointing upwards must be read in a clockwise direction; triangles pointing downwards in a counterclockwise direction. This additional complication results from the authors’ definition of the axes of the Tonnetz as interval-classes. The sia of a sc exhibits its proper configuration only when the pcs involved are arranged in ascending adjacent order and the ordered intervallic distance is calculated. A sia does not invoke the concept of ic. Any triangle pointing upwards, then, must be read clockwise in order to yield a form of the sia <1-2-9>: reading the same triangle counterclockwise and calculating the ordered intervallic distance produces the interval series e-t-3, the inverses of ordered intervals 1-2-9. Having ics along the axes of the Tonnetz would not cause a problem if the subject of the model were not this 3-2 Cohn cycle that depends on the concept of a sia for its definition and construction. Therefore, the axes on the Tonnetz cannot be bidirectional as their identity as ics suggests. This aspect of the model further obscures the presence of a Cohn cycle on Reed and Bain’s Tonnetz and is in fact a more serious flaw. Even though they are difficult to isolate, Cohn flip relationships are still present on the Tonnetz given an appropriate interpretation. The ics along the axes of the Tonnetz, however, cannot be reconciled to Lewin’s theory of a Cohn function derived from a sia, as we have here.
[17] Reed and Bain prefer their Tonnetz because it is less open to misconstruction than Lewin’s graph—recall that their criticisms are based primarily on its immediate visual accessibility. In the end, however, the Tonnetz design is less successful since it alleviates only superficial and personal aesthetic concerns while at the same time making its relationship to its subject, a theoretically conceived Cohn cycle, more difficult to determine. Instead of clarifying Cohn cycles and Cohn functions, the Tonnetz model at best remains on par with Lewin’s graph, and at worst even obfuscates the theory.
Conclusion
[18] In my comparison of the models, I have isolated their iconic components (the nodes and axes) and have considered how each relates to the 3-2 Cohn cycle. A successful model in music theory, I believe, incorporates iconic components that correspond as closely as possible to elements of the theory it concretizes. In this regard, the axes of the Tonnetz are not labeled adequately. Because the axes are directionally unspecified and represent ics instead of ordered intervals, Reed and Bain have missed a crucial component of Lewin’s description of the 3-2 Cohn cycle as generated by performing Cohn flips on the Cohn function derived from the sia of sc 3-2. Ultimately, both models show the same results but from different perspectives. On the surface, each reveals the same pc content of the sc 3-2 trichords within the Cohn cycle, but the Tonnetz is not a model of the 3-2 Cohn cycle in the same respect as Lewin’s graph. With the Tonnetz design’s ambiguity regarding the order of the sias and the tension between ics and ordered-interval series, the 3-2 Cohn cycle, in the sense that Lewin depicted it, is more a byproduct or consequence of Reed and Bain’s model instead of its primary subject.
[19] The central difficulty in evaluating a music theory model, I believe, is separating the attributes it has as a visual design from those that bear an analogical relationship to the model’s subject. The Tonnetz is readily grasped from a visually aesthetic perspective, especially in its elimination of common dyad duplication. Achieving this aesthetic standard, however, should not inform any model’s evaluation, and in this case is deceptively attractive. Lewin’s graph, while perhaps visually cruder than the Tonnetz, exhibits a more clear and direct representation of the 3-2 Cohn cycle with the clear one-to-one correspondence of its iconic components to elements of the theory. Iconic models in music theory should be evaluated for their effectiveness in rendering visible and, in a way, reifying the essentially unobservable nature of their theoretical subjects. In this way, iconic models in music theory fulfill their purpose of explaining and clarifying abstract theoretical concepts.
[20] Studies in the Philosophy of Science devote the most attention to models.(12) Even though iconic models pervade music theory literature, we encounter few comprehensive analyses of music theory models that describe how they work as models per se and how they relate to their subjects. This paper certainly raises more questions than it answers, particularly concerning the nature of the analogical relationship between model and subject, the explanatory function of models, and the incorporation of conventional metaphor in their iconic design. I only hope to have offered a different perspective than Reed and Bain have in the comparison of Lewin’s graph of the 3-2 Cohn cycle with its Tonnetz representation.
Michael Fitzpatrick
University of Western Ontario
mfitzpa7@uwo.ca
Works Cited
Chrisman, Richard. 1977. “Describing Structural Aspects of Pitch-Sets Using Successive-Interval Arrays.” Journal of Music Theory 21: 1–28.
Cohn, Richard. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41: 1–66.
—————. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions. Music Analysis 15: 9–40.
Harré, Rom. 1970. The Principles of Scientific Thinking. Chicago: University of Chicago Press.
Hesse, Mary. 1966. Models and Analogies in Science. Notre Dame, Indiana: University of Notre Dame Press.
Johnson, Jeffrey. 1997. Graph Theoretical Models of Abstract Musical Transformation. Westport, Connecticut: Greenwood Press.
Lewin, David. 1998. “Notes on the Opening of the F? Minor Fugue from WTCI.” Journal of Music Theory 42: 235–239.
—————. 1996. “Cohn Functions.” Journal of Music Theory 40: 181–216.
Morris, Robert D. 1987. Composition with Pitch-Classes: A Theory of Compositional Design. New Haven and London: Yale University Press.
Nolan, Catherine. 2007. “Thoughts on Klumpenhouwer Networks and Mathematical Models: The Synergy of Sets and Graphs.” Music Theory Online 13.3.
Reed, Jacob and Matthew Bain. 2007. “A Tetrahelix Animates Bach: Revisualization of David Lewin’s Analysis of the Opening of the F-sharp Minor Fugue from WTC I.” Music Theory Online 13.4.
Footnotes
1. Iconic models employ visual images, as opposed to mathematical or computer models.
Return to text
2. In fairness to Reed and Bain’s work, I must qualify that the authors never explicitly use language like I have here to assert the superiority of their model over Lewin’s. This attitude is revealed, however, in certain phrases and comparative language that Reed and Bain use to describe both models: e.g. Lewin’s layout makes it “difficult to imagine the music progressing through the graph,” has a format that “disjoins these [Cohn flip] relations,” is “difficult to visually process quickly,” is “harder to read”; and the Tonnetz model “succeeds in restructuring the trichords,” is “a more accurate representation,” “resolves the issues of repetition and order,” and shows pcsets “no longer forced into an arbitrary hierarchy” (Reed and Bain 2007, [1.2]-[1.4]).
Return to text
3. I agree with Reed and Bain that neither Lewin’s graph nor the Tonnetz they construct is adequate for animating Bach’s fugue in a three-dimensional pitch-space that accounts for registral distinctions. What I address in this commentary is the authors’ contention that the Tonnetz is a better model of the 3-2 Cohn cycle.
Return to text
4. In Figure 2, the graph mixes upper case with lower case pc letters. While this is important for Lewin’s analysis of the F-sharp Minor fugue, we need not consider the difference in case here.
Return to text
5. For an introduction to the components and design of graphic networks and their application in music theory, see Johnson 1997 and Nolan 2007.
Return to text
6. For a full description and explanation of Cohn flips, Cohn functions, and Cohn cycles see Lewin 1996. In this paper, I adopt the following notation: <1-2-9> indicates a successive-interval array; (129) indicates the Cohn function derived from it. The (129) Cohn function is merely a specific interpretation of the sia <1-2-9>; but it becomes necessary to distinguish between these theoretical perspectives of what is essentially the same thing.
Return to text
7. See Chrisman 1977 and Morris 1987 for a detailed description of successive-interval arrays and their independence from particular pc instantiations of a sc. Here, Lewin integrates as closely as possible Cohn flips upon pcsets that exchange adjacent pcs with the theory of Cohn functions. This corresponds to the order in which Lewin presents his material in “Cohn Functions”: the definition and demonstration of Cohn flips upon pcsets precedes and helps define a Cohn function as a function that may be Cohn-flipped analogously.
Return to text
8. Reed and Bain color certain areas of the Tonnetz just as Lewin includes both upper and lower case letters. As before, this feature of the Tonnetz need not inform the present discussion.
Return to text
9. Incidentally, Lewin’s Example 7 is the prototype of the graphs that appear as Figures 1 and 2 of this paper. As such, we understand the sia of each pcset on these graphs as implicitly contained within each trichordal node of the network.
Return to text
10. Lewin 1996 discusses Cohn cycles of pcsets before introducing Cohn cycles of Cohn functions and the two concepts are closely connected. Lewin’s 3-2 Cohn cycle graph cannot be a Cohn cycle of pcset 3-2, however, since the exchange between trichords on the graph is not always by adjacent pcs.
Return to text
11. The {FD
Return to text
12. For an introduction to model theory in the Philosophy of Science, see Hesse 1966 and Harré 1970.
Return to text
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits: