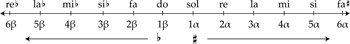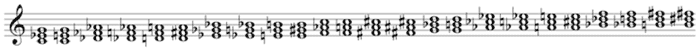The Expansion of the Concept of Mode in Twentieth-Century Russian Music Theory
Inessa Bazayev
KEYWORDS: Russian music theory, mode, twelve-tone diatonicism, Shostakovich, Prokofiev, Ogolevets, Dolzhanskiĭ, Skorik, Kholopov
ABSTRACT: In Russian music theory, the concept of lad (mode) plays a central role in understanding non-tonal Russian music. There is no equivalent term in the West to explain Russian lad. Although early definitions simply described it as a diatonic scale, the term was later expanded, altered, and applied to non-tonal music of Scriabin, Prokofiev, and Shostakovich. Lad applies not only to the traditional church or Greek modes, but also to alterations thereof, as well as newly created modes, where orthography often determines the function of a single pitch. I explore the ever-changing concept of lad in the writings of prominent Russian theorists Alexeï Ogolevets, Alexander Dolzhanskiĭ, Miroslav Skorik, and Iuriĭ Kholopov, and I show how the concept enables discussion of non-tonal music, first from functional and then from voice-leading perspectives. The Russian analyses highlight continuity between twentieth-century repertoires and music from the common-practice era.
Copyright © 2014 Society for Music Theory
[1.1] In Russian music theory, the concept of mode (lad) plays a central role in understanding twentieth-century music.(1) In this article, I survey definitions of mode in prominent theoretical works of Alexeï Ogolevets, Alexander Dolzhanskiĭ, Miroslav Skorik, and Iuriĭ Kholopov and explore the use of modal concepts in Russian analyses of twentieth-century Russian music.
[1.2] In describing modality in Shostakovich’s music, Ellon Carpenter notes: “The Russian concept of mode has no exact equivalent in Western music theory” (1995, 76).(2) Although early definitions simply described modes as diatonic scales, later definitions expanded and altered the concept, applying it to the non-tonal music of Scriabin, Prokofiev, and Shostakovich. Further, through the history of the term, mode has applied not only to the traditional church modes (Dorian, Phrygian, Aeolian, etc.) but also to alterations thereof, as well as newly created modes. In the subject entry for mode (lad) in Music Encyclopedia, Kholopov (1976) describes its three important features: (1) each mode is built on a scale, (2) pitches in the scale may be stable or unstable, and (3) each mode has an intonation (intonatsiia), or an emotional, social, and historical connection. Pitch function—the relative stability and instability of pitches—is crucial in earlier writings on mode (Ogolevets 1941 and Dolzhanskiĭ 1947). However, in later writings (Skorik 1962, 1969; Kholopov 1981, 1988), pitch function is loosely defined and increasing attention is given to voice leading. This voice-leading approach is extensively applied to chromatic passages in Prokofiev’s music (e.g., Romeo and Juliet), non-tonal works of Nicolai Roslavets (e.g., selected songs), and other twentieth-century Russian repertoires. It leads to the concept of twelve-tone tonality and Kholopov’s hemitonic (semitonal) system. Thus, the emphasis on chromatic voice leading in later writings goes along with increased attention to harmonies, rather than to individual pitches.
Pitch Function in Lad: The Writings of Ogolevets and Dolzhanskiĭ
Example 1. Ogolevets’s line of fifths
(click to enlarge)
Example 2. Different possibilities for the resolution of augmented prime (Ogolevets 1941, 343)
(click to enlarge)
Example 3. Resolution of two augmented primes—G/
(click to enlarge and listen)
Example 4. Opening theme from Shostakovich’s Piano Sonata no. 2, I
(click to enlarge and listen)
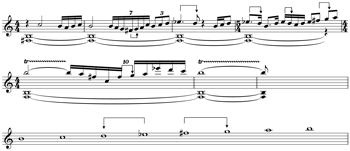
[2.1] In his monumental work Osnovy garmonicheskogo iazyka (Foundations of harmonic language) (1941), Alexeï Ogolevets describes “twelve-tone tonality” (dvenadtsati-zvukovaia tonal’nost’) as an extension of tonality built along the line of diatonic perfect fifths. Example 1 reproduces Ogolevets’s line of fifths; alpha represents the sharp side and beta represents the flat side, which starts at C (Ogolevets 1941, 85).(3) Any given key can be expanded with inflected (lowered or raised) scale degrees to include neighboring and more distant keys on the line of fifths. Even within twelve-tone tonality, orthography is important, for each scale degree functions within the given key. There is always an attraction (tiagotenie) among the pitches: a lowered note resolves downward, and a raised note resolves upward. Further, within this system Ogolevets regarded the unison as the most consonant interval and the augmented prime as the most dissonant interval. Example 2 shows different possibilities for the resolution of augmented prime (Ogolevets 1941, 343), and Example 3 shows the resolution of two augmented primes—G/
[2.2] Unfortunately, Ogolevets’s rule of proper resolution of the augmented prime does not hold for other works by Prokofiev or his Russian contemporaries. Example 4 shows the opening theme from Shostakovich’s Piano Sonata no. 2, I, with the simultaneous sounding of B and
[2.3] One of the most interesting features of Ogolevets’s treatise is the classification of different seven-note collections into four families of mode. Table 1a reproduces Ogolevets’s table in the original Russian (Ogolevets 1941, 726–27); Table 1b provides my translation. The table classifies modes into four families, each with eight modes: family 1 consists of “harsh” major and minor modes (the “harsh” modes have lowered and raised ), family 2 consists of Lydian modes, family 3 consists of Phrygian modes, and family 4 consists of major and minor modes that are not part of family 1. The third scale degree of the mode is the main determinant of the major and minor quality of that mode.(6) This is quite important for Ogolevets’s theory, since even non-tonal music (i.e., music without functional harmony) may be associated with tonal elements (major and minor modes), providing continuity with the music from the common-practice era.(7)
Table 1a. Ogolevets’s Four Families of Mode (click to enlarge) | Table 1b. Ogolevets’s Four Families of Mode (bazayev_example_info.php) |
Example 5. Solo flute part from Shostakovich’s Symphony no. 6, I
(click to enlarge and listen)
[2.4] The concept of mode and its relation to common–practice tonality permeates the work of Alexander Dolzhanskiĭ (1947; 1962), a prominent Shostakovich scholar. Unlike Ogolevets’s theory, Dolzhanskiĭ’s work is driven by actual musical examples. Dolzhanskiĭ notes that Shostakovich created new modes by altering scale degrees from the traditional church modes. Dolzhanskiĭ divides his modes into two categories: lowered and doubly lowered (category 1), and raised and doubly raised (category 2). Lowered modes comprise “minor” church modes (Phrygian, Aeolian, and Dorian) with lowered ; and doubly lowered modes comprise the minor church modes with lowered and (Dolzhanskiĭ 1962, 27–29). Example 5 shows the solo flute part from Shostakovich’s Symphony no. 6, I, which Dolzhanskiĭ describes as lowered B–Phrygian, or Phrygian mode with lowered : B–C–D–
Example 6. Theme from the last movement of Shostakovich’s Piano Sonata no. 2
(click to enlarge and listen)
Example 7. Dolzhanskiĭ’s doubly lowered Phrygian mode
(click to enlarge and listen)
Example 8. Dolzhanskiĭ’s raised
(click to enlarge and listen)
[2.5] The doubly lowered mode is one of Dolzhanskiĭ’s most fascinating concepts. Example 6 shows the theme from the last movement of Shostakovich’s Piano Sonata no. 2, which is based on Dolzhanskiĭ’s doubly lowered B–Aeolian mode: B–
[2.6] Example 7 shows another instance of Dolzhanskiĭ’s doubly lowered Phrygian mode Dolzhanskiĭ (1962, 29). The example illustrates a doubly lowered E-Phrygian mode in the flute solo from the coda of Shostakovich’s Symphony no. 5. Even though the lowered and fall on strong downbeats, they function in the traditional manner: both the
[2.7] Dolzhanskiĭ’s raised modes are seven–note scales based on the “major” church modes (Ionian, Lydian, or Mixolydian) with raised (Dolzhanskiĭ 1962, 40). Example 8 shows Dolzhanskiĭ’s raised
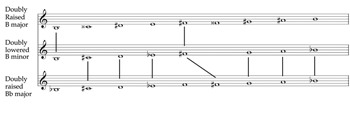
Example 9. Dolzhanskiĭ’s three common-tonic keys (odnoimmenye tonal’nosti)
(click to enlarge)
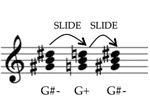
[2.8] Dolzhanskiĭ goes on to show common-tone relationships between raised and lowered modes. Example 9 shows Dolzhanskiĭ’s three common-tonic keys (odnoimmenye tonal’nosti) (Dolzhanskiĭ 1962, 41). The doubly raised B major (with raised and ) at the top of the example has two common tones with its “parallel” minor—doubly lowered B minor.(10) On the other hand, there are seven common tones between the bottom two scales, doubly lowered B minor and doubly raised
Voice Leading in Lad: The Writings of Skorik and Kholopov
[3.1] While Ogolevets’s and Dolzhanskiĭ’s modes involve alterations of scale degrees in traditional church modes, Prokofiev scholar Miroslav Skorik describes an expanded “synthetic mode,” which enriches and widens a single tonality by “twelve-tone diatonicism” (dvenadtistupennaia diatonika) (Skorik 1969, 24). (This concept is analogous to Ogolevets’s twelve-tone tonality.) Pitch function (i.e., the directional tendency of tones) becomes less important for Skorik, and semitonal voice leading becomes essential. The function of harmonies and the connection between them take precedence over the function of individual scale degrees.
Example 10. Skorik’s twelve-tone diatonic mode in Prokofiev’s music (click to enlarge) |
Example 11a. Skorik’s twelve-tone diatonic system in Prokofiev’s Stone Flower
(click to enlarge and listen)
Example 11b. Parsimonious voice leading between the I and bvi chords
(click to enlarge)
[3.2] Example 10 shows Skorik’s twelve-tone diatonic mode in Prokofiev’s music, here in an expanded key of C major (Skorik 1969, 72). Major and minor triads are built on each scale degree, and most of the scale degrees are instantiated by two pitch classes. The second scale degree, for example, has major and minor triads built on both
Example 12a. Opening measures of “Juliet as a Young Girl” from Prokofiev’s Romeo and Juliet (Skorik 1969, 74) (click to enlarge and listen) | Example 12b. Voice-leading reduction of the opening measures of “Juliet as a Young Girl” from Prokofiev’s Romeo and Juliet (click to enlarge) |
Example 13a. Excerpt from Prokofiev’s Sonata no. 6, IV (Skorik 1969, 76–77)
(click to enlarge and listen)
Example 13b. Voice-leading reduction of excerpt from Prokofiev’s Sonata no. 6, IV
(click to enlarge)
[3.3] Similar parsimonious progressions characterize all the musical examples discussed by Skorik. Example 12a shows the opening measures of “Juliet as a Young Girl” from Prokofiev’s Romeo and Juliet (Skorik 1969, 74). Skorik’s approach considers all harmonies (including
[3.4] Functional relations among the pitches become further loosened in Iuriĭ Kholopov’s writings on mode. In his influential textbook Garmoniia (Harmony), Kholopov discusses his hemitonic system (or the system of counting half steps), which is similar to the Western system of a set-class analysis (Kholopov 1981, 100–26; see also Cairns 2014 and Ewell 2013). Example 14 shows an excerpt from Rimsky-Korsakov’s Sadko (Kholopov 1988, 212–13). From a set-theoretical perspective, the passage is completely based on OCT0,1. However, in Kholopov’s more differentiated analysis, the passage is based on two modes: mode 1.3.2.1.3.2 (with successive interval classes 1, 3, 2, etc.) and mode 1.2.1.2.1.2.1.2 (the octatonic scale beginning with a semitone).(17) Neither pitch nor chord function is of any significance; rather, the modes are defined and identified by their pitch content. Kholopov’s analysis seems to show a Russian version of the emancipation of dissonance as the “emancipation of mode.” Example 15 shows Kholopov’s analysis of Nicolaĭ Roslavets’s song “Ty ne ushla” (Kholopov 1981, 109–13). This work is clearly not tonal. Consequently, Kholopov does not use any Roman numerals, but rather he defines the main set or “grouppa” (group) that makes up the work (shown in the lowest stave in measure 1). Further, Kholopov uses the hemitonic system to identify this group as 1.3.1.2.1, an equivalent of set class [013478].(18) This group is subsequently transposed, mostly by major and minor thirds, as well as perfect fourths and fifths; Kholopov identifies the bottom note (i.e., “root”) of each mode by its note name.(19) Kholopov’s analysis is intriguing in two ways: (1) he refers to each abstracted scale as a lad (or mode) that is made up of group 1.3.1.2.1; and (2) following Ogolevets’s method, Kholopov tries to give tonal quality to the set. In measure 1, under the first group (or set) he indicates
Example 14. Excerpt from Rimsky-Korsakov’s Sadko (Kholopov 1988, 212–13) (click to enlarge and listen) | Example 15. Kholopov’s analysis of Nicolaĭ Roslavets’s song “Ty ne ushla” (Kholopov 1981, 109–13) (bazayev_example_info.php) |
Conclusion
[4.1] Mode plays a crucial role in the Russian theoretical approach to the chromatic tonal music of both Shostakovich and Prokofiev, as well as the non-tonal music of Nicolai Roslavets. By using a single “catch-all” term—lad (or mode)—Russian theorists are able to discuss both highly chromatic tonal music, as well as non-tonal music, in terms of scalar collections and scale degrees. While orthography defines modes in writings from the first half of the twentieth century (Ogolevets and Dolzhanskiĭ), parsimonious relationships among the harmonies dominate the writings of the second half of the twentieth century (Kholopov and Skorik). Even without functional relationships, mode remains an integral part of Russian theoretical thought, creating the perception of continuity with music from the common-practice era. This approach allows us to reevaluate and reconsider our understanding of Russian twentieth-century music.
Inessa Bazayev
Louisiana State University
College of Music and Dramatic Arts
102 School of Music
Baton Rouge, LA 70803
ibazayev@lsu.edu
Works Cited
Bazayev, Inessa. 2013. “Triple Sharps, Qnt Relations, and Symmetries: Orthography in the Music of Nicolaĭ Roslavets.” Music Theory Spectrum 35, no. 1: 111–31.
Beliaev, Viktor. 1923. “Mekhanika ili logika?” [Mechanism or logic?]. K novym beregam, Vol. 3: 21–30.
Cairns, Zachary A. 2014. “A Glimpse at Iuriĭ Kholopov’s Garmonicheskiĭ analiz.” Music Theory Online 20, no. 3.
Carpenter, Ellon D. 1995. “Russian Theorists on Modality in Shostakovich’s Music.” In Shostakovich Studies, ed. David Fanning, 76–112. Cambridge: Cambridge University Press.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1: 9–40.
—————. 1998. “Introduction to Neo-Riemannian Theory.” Journal of Music Theory 42 no. 2: 167–80.
—————. 2004. “Uncanny Resemblances: Tonal Signification in the Freudian Age.” Journal of the American Musicological Society 57, no. 2: 285–323.
Dolzhanskiĭ, Alexandr. 1947. “O ladovoï osnove sochineniĭ Shostakovicha” [On modal premise in the works of Shostakovich]. Sovetskaia muzyka no. 4: 65–74. Reprinted in Cherty stilia D. Shostakovicha [Stylistic characteristics in (the music of) D. Shostakovich], ed. Lev Mazel’, 24–42. Moscow: Soveremennyĭ kompozitor, 1962.
—————. 1962. “O ladovoi osnove sochinenii Shostakovicha” [On modal foundation in Shostakovich’s works]. In Cherty stilia D. Shostakovicha: sbornik teoreticheskikh stateĭ [The features of Shostakovich’s style: a collection of theoretical articles], ed. Lyubov’ Berger. Moscow: Sovetskii Kompozitor, 24–42.
Ewell, Philip. 2013. “Russian Pitch-Class Set Analysis and the Music of Webern.” Gamut: Online Journal of the Music Theory Society of the Mid-Atlantic 6, no. 1: 219–76.
Iavorskiĭ, Boleslav Leopol’dovich. 1908. Stroenie muzykal’noĭ rechi [The construction of musical speech]. Moscow: Gos. Iz-vo.
—————. 1915. Uprazhneniia v obrazovanii ladovogo ritma [Exercises in the formation of schemes of modal rhythm]. Moscow: Gos. Iz-vo.
Kholopov, Iuriĭ Nikolaevich. 1976. “Lad” [Mode]. Muzykal’naia entsiklopediia [Music encyclopedia], vol. 3, cols. 130–43. Moscow: Sovetskaia entsiklopediia.
—————. 1981. “Problema novoĭ tonal’nosti v Russkom i Sovetskom teoreticheskom muzykoznaniĭ” [The Problem of new tonality in Russian and Soviet music theory]. In Voprosy metodologii Sovetskogo muzykoznanii [Questions of Soviet musical methodology], ed. A. I. Kandinskiĭ, 100–26. Moscow: Moskovskaia gos. konservatoriia im. P.I. Chaikovskogo.
—————. (1988). Garmoniia [Harmony]. Moscow: Muzyka.
Lewin, David. [1987] 2007. Generalized Musical Intervals and Transformations. New York: Oxford University Press.
Mazel’, Lev. 1957. “O razhshirenii poniatiia odnoimennoĭ tonal’nosti” [On the development of the concept of parallel keys]. Sovetskaia muzyka no. 2: 141–45.
—————. 1960. Simfonii D.D. Shostakovicha [Shostakovich’s symphonies]. Moscow: Sovetskiï kompozitor.
Ogolevets, Alexeĭ. 1941. Osnovy garmonicheskogo iazyka [Foundations of harmonic language]. Moscow-Leningrad: Gosudarstvennoe muzykal’noe izdatel’stvo.
Powers, Harold. 2001. “Mode.” The New Grove Dictionary of Music and Musicians, ed. Stanley Sadie, 2nd edition, vol. 16, 775–823. London: McMillan Publishers.
Roslavets, Nicolai. 1927. “Novaia sistema organizatsii zvuka i novye metody prepodavaniia teorii kompozitsii: tezisy doklada” [The new system of tone organization and new methods of teaching the theory of composition: theses of lectures]. Unpublished lecture, Moscow.
Skorik, Miroslav. 1962. “Prokof’ev i Shenberg” [Prokofiev and Schoenberg]. Sovetskaia muzyka no. 1: 34–38.
—————. 1969. Ladovaia sistema S. Prokof’eva [S. Prokofiev’s Modal System]. Kiev: Muzichna Ukraina.
Taruskin, Richard. 2011. “Catching Up with Rimsky-Korsakov.” Music Theory Spectrum 33, no. 2: 169–85.
Tymoczko, Dmitri. 2011. A Geometry of Music. New York: Oxford University Press.
Discography
Discography
Prokofiev, Sergei. 2011. Mussorgsky: Pictures at an Exhibition; Prokofiev: Piano Sonata no. 7 and Piano Concerto no. 1. Perf. Sviatoslav Richter and Prague Symphony Orchestra. Cond. Karel Ancerl. Regis Records, compact disc.
—————. 2005. The Tale of the Stone Flower. Perf. Bolshoi Orchestra. Cond. Gennady Rozhdestvensky. FSUE “Firma Melodia.”
—————. 2003. Romeo and Juliet: Complete Suite from the Ballet. Perf. Cincinnati Symphony Orchestra. Cond. Paavo Järvi. Telarc International Group, compact disc.
—————. 1994. Piano Sonatas nos. 4 and 6. Perf. Yefim Bronfman. Sony Classics, compact disc.
Rimsky-Korsakov, Nikolai. 2008. Sadko. Perf. Bolshoi Orchestra and Bolshoi Chorus. Cond. Evgeny Svetlanov. Opera d’Oro, compact disc.
Roslavets, Nikolai. 2011. “Ty ne ushla” [You didn’t leave]. Perf. Jennifer Crippen, mezzo-soprano, and Kristin Eliason, piano. Recital Hall, Louisiana State University.
Shostakovich, Dmitri. 2006. Shostakovich: Piano Sonata no. 2, The Limpid Stream, and A Child’s Exercise Book. Perf. Konstantin Scherbakov. Naxos, compact disc.
—————. 1983. Shostakovich: The Complete Symphonies [Box Set]. Perf. Royal Concertgebouw Orchestra and London Philharmonic Orchestra. Cond. Bernard Haitink. Decca, compact disc.
Footnotes
1. The Russian theorist who began a systematic study of mode in twentieth-century Russian music (especially, the music of Scriabin) was Boleslav Iavorskiĭ. See Iavorskiĭ 1908 and 1915.
Return to text
2. For a fairly recent Western interpretation of mode, see Powers 2001. Although the Russian concept of mode shares some similarities with the Western concept of mode that includes church or Greek modes, Russian theorists often apply the term to special collections (e.g., whole-tone, octatonic, etc.), as well as newly created modes on which a given composition would be based (e.g., Scriabin’s Prometheus chord).
Return to text
3. The solfège here and throughout represents absolute pitch; do=C, re=D, and so forth.
Return to text
4. The remainder of the opening of Prokofiev’s Piano Concerto no. 1 (through R3) continues to feature augmented primes.
Return to text
5. The resolution of the augmented prime moves outward to an interval of a major third. Please note that the whole-step motion from B to
Return to text
6. The idea of major and minor quality classification becomes crucial to Soviet twentieth-century composers (including Prokofiev and Shostakovich), who use these tonal designations to enable experiments with non-tonal elements, including special collections (e.g., octatonic) and non-tonal motivic relationships.
Return to text
7. Ogolevets’s table is rather cumbersome. Even though his description of the four families and their individual modes is very telling of his approach—in particular, he qualifies each mode as major or minor—Ogolevets does not show the occurrence of any of his modes in actual musical passages. The examples that he does use are usually very short (as in the Prokofiev example above) and they illustrate one isolated theoretical idea without any larger interpretation. Some of the modes also do not reflect musical practice because he assumes that each scale must have seven pitches. For instance, in the case of the Prometheus chord (Scriabin’s so-called “Mystic” chord), Ogolevets identifies the mode as do-re-mi-fa
Return to text
8. It is also important to note the two doubly diminished 4ths (B to
Return to text
9. Dolzhanskiĭ also discusses diminished minor modes, but he doesn’t give actual musical examples. A diminished minor mode consists of a minor mode that includes four diminished intervals with the tonic: the diminished 4th, 5th, 7th, and 8ve (Dolzhanskiĭ 1962, 34–35).
Return to text
10. In the example reproduced here as Example 9, Dolzhanskiĭ includes both raised and diatonic . Although he doesn’t explain their co-existence, he is probably trying to highlight the importance of the dominant within a key. Even if is often raised in a double raised major, a diatonic is possible, for it is the root of the dominant harmony.
Return to text
11. The idea of common tonic or parallel keys (odnoimennoe tonal’nost’) is prominent in the writings of Lev (Leo) Mazel’ (1957). Mazel’ discusses the relation between two keys related to each other by a half step in Liszt’s “Forgotten Waltz” in F-sharp minor. Mazel’ also goes on to discuss the importance of common-third relations in triads, which predates the neo-Riemannian transformation SLIDE (see Lewin 1987, 178). The concept of lowered scale degrees is also discussed in Tymoczko 2011, 329–32. In his analysis of Shostakovich’s Prelude and Fugue in F-sharp minor, Tymoczko presents a background set of scales based on
Return to text
12. Skorik adds that non-tertian harmonies are also possible within this system, but he does not discuss them in any detail.
Return to text
13. Of course, this kind of motion also characterizes passages from Schubert’s works that include the Der Gondelfahrer, D. 809.
Return to text
14. This is a progression between “hexatonic poles” (see Cohn 2004). The fact that Skorik includes it within a single “diatonic” key thus indicates the degree to which his theory expands the concept of key. The changing emphasis in Russian concepts of mode, from a focus on the tendency of individual pitches to a focus on voice leading, is itself embedded—in Cohn’s description—within this individual progression (Cohn 2004, 303–8). The pitches of each triad are tendency tones in relation to the other triad, but each is also a consonant triad (i.e., the
Return to text
15. See Cohn 1996 for an introduction to hexatonic cycles.
Return to text
16. From a Schenkerian perspective, the G-major harmonies can be explained as neighboring chords to the tonic triad (
Return to text
17. While I would classify the passage as based on Kholopov’s mode 1.2.1.2.1.2.1.2, Kholopov’s own analysis seems to be more detailed, favoring blow-by-blow examination. Further, Kholopov re-brands the octatonic scale as lad 1.2.1.2.1.2.1.2, in order to be consistent with his hemitonic system. However, Kholopov refers to this scale as either lad Rimskogo-Korsakova (Rimsky-Korsakov’s mode) or gamma ton-poluton (tone- and half-tone scale) (Kholopov 1988, especially 208–13). These terms (lad Rimskogo-Korsakova and gamma ton-poluton) are used interchangeably throughout Kholopov’s influential textbook Garmoniia (1988), as well as other writings, including those on Stravinsky’s music. Kholopov’s terminology supports Richard Taruskin’s argument that the scale was discovered by Rimsky-Korsakov in Liszt’s music, used by Rimsky-Korsakov (in his own compositions), and taught to his students, including Stravinsky (Taruskin 2011, 175–76). The term gamma ton-poluton continues to be used today in Russian conservatories and musical circles more frequently, and it is understood to have its Russian origins in the music of Rimsky-Korsakov.
Return to text
18. The main similarity between Kholopov’s hemitonic system and set-class analyses lies in the ascending order of intervals and their ability to be transposed to begin on any pitch (à la normal form). However, unlike set-class analysis, the hemitonic system does not assume inversional equivalence.
Return to text
19. For more on Roslavets’s compositional system, and especially the significance of orthography in his music, see Bazayev 2013.
Return to text
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
18422